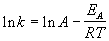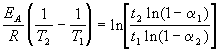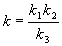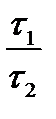Связь уравнения вант гоффа и уравнения аррениуса

Видео:Задачи на правило Вант-Гоффа. Зависимость скорости реакции от температуры.Скачать

Связь уравнения вант гоффа и уравнения аррениуса

Из качественных соображений понятно, что скорость реакций должна увеличиваться с ростом температуры, т.к. при этом возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение. Для количественного описания температурных эффектов в химической кинетике используют два основных соотношения — правило Вант-Гоффа и уравнение Аррениуса.

Правило Вант-Гоффа заключается в том, что при нагревании на 10 о С скорость большинства химических реакций увеличивается в 2 4 раза. Математически это означает, что скорость реакции зависит от температуры степенным образом:

, (4.1)

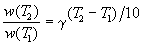
где — температурный коэффициент скорости ( = 24). Правило Вант-Гоффа является весьма грубым и применимо только в очень ограниченном интервале температур.

Гораздо более точным является уравнение Аррениуса, описывающее температурную зависимость константы скорости:

, (4.2)

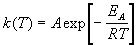
где R — универсальная газовая постоянная; A — предэкспоненциальный множитель, который не зависит от температуры, а определяется только видом реакции; E_A — энергия активации, которую можно охарактеризовать как некоторую пороговую энергию: грубо говоря, если энергия сталкивающихся частиц меньше E_A, то при столкновении реакция не произойдет, если энергия превышает E_A, реакция произойдет. Энергия активации не зависит от температуры.

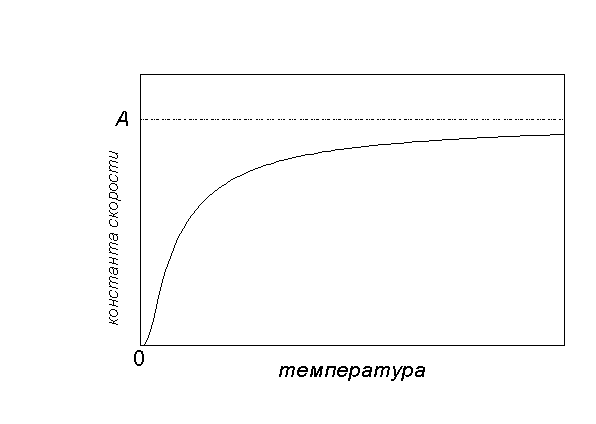
Графически зависимость k(T) выглядит следующим образом:

При низких температурах химические реакции почти не протекают: k(T) 0. При очень высоких температурах константа скорости стремится к предельному значению: k(T) A. Это соответствует тому, что все молекулы являются химически активными и каждое столкновение приводит к реакции.

Энергию активации можно определить, измерив константу скорости при двух температурах. Из уравнения (4.2) следует:

. (4.3)

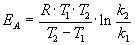
Более точно энергию активации определяют по значениям константы скорости при нескольких температурах. Для этого уравнение Аррениуса (4.2) записывают в логарифмической форме

и записывают экспериментальные данные в координатах ln k — 1/T. Тангенс угла наклона полученной прямой равен —E_A / R.

Для некоторых реакций предэкспоненциальный множитель слабо зависит от температуры. В этом случае определяют так называемую опытную энергию активации:

. (4.4)

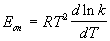
Если предэкспоненциальный множитель — постоянный, то опытная энергия активации равна аррениусовской энергии активации: E_оп = E_A.

Пример 4-1. Пользуясь уравнением Аррениуса, оцените, при каких температурах и энергиях активации справедливо правило Вант-Гоффа.

Решение. Представим правило Вант-Гоффа (4.1) как степенную зависимость константы скорости:

,

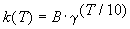
где B — постоянная величина. Сравним это выражение с уравнением Аррениуса (4.2), приняв для температурного коэффициента скорости значение

.

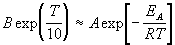
Возьмем натуральный логарифм обеих частей этого приближенного равенства:

.

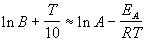
Продифференцировав полученное соотношение по температуре, найдем искомую связь связь между энергией активации и температурой:

.

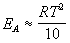
Если энергия активации и температура примерно удовлетворяют этому соотношению, то правилом Вант-Гоффа для оценки влияния температуры на скорость реакции пользоваться можно.

Пример 4-2. Реакция первого порядка при температуре 70 о С завершается на 40% за 60 мин. При какой температуре реакция завершится на 80% за 120 мин, если энергия активации равна 60 кДж/моль?

Решение. Для реакции первого порядка константа скорости выражается через степень превращения следующим образом:

,

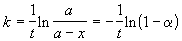
где a = x/a — степень превращения. Запишем это уравнение при двух температурах с учетом уравнения Аррениуса:

,

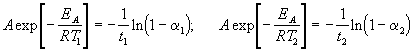
где E_A = 60 кДж/моль, T₁ = 343 K, t₁ = 60 мин, a ₁ = 0.4, t₂ = 120 мин, a ₂ = 0.8. Поделим одно уравнение на другое и прологарифмируем:

Подставляя в это выражение приведенные выше величины, находим T₂ = 333 К = 60 о С.

Пример 4-3. Скорость бактериального гидролиза мышц рыб удваивается при переходе от температуры -1.1 о С к температуре +2.2 о С. Оцените энергию активации этой реакции.

Решение. Увеличение скорости гидролиза в 2 раза обусловлено увеличением константы скорости: k₂ = 2k₁. Энергию активации по отношению констант скорости при двух температурах можно определить из уравнения (4.3) с T₁ = t₁ + 273.15 = 272.05 K, T₂ = t₂ + 273.15 = 275.35 K:

130800 Дж/моль = 130.8 кДж/моль.

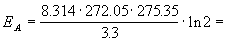
4-1. При помощи правила Вант-Гоффа вычислите, при какой температуре реакция закончится через 15 мин, если при 20 о С на это требуется 2 ч. Температурный коэффициент скорости равен 3.(ответ)

4-2. Время полураспада вещества при 323 К равно 100 мин, а при 353 К — 15 мин. Определите температурный коэффициент скорости.(ответ)

4-3. Какой должна быть энергия активации, чтобы скорость реакции увеличивалась в 3 раза при возрастании температуры на 10 0 С а) при 300 К; б) при 1000 К?(ответ)

4-4. Реакция первого порядка имеет энергию активации 25 ккал/моль и предэкспоненциальный множитель 5 . 10 13 сек -1 . При какой температуре время полураспада для данной реакции составит: а) 1 мин; б) 30 дней?(ответ)

4-5. В каком из двух случаев константа скорости реакции увеличивается в большее число раз: при нагревании от 0 о С до 10 о С или при нагревании от 10 о С до 20 о С? Ответ обоснуйте с помощью уравнения Аррениуса.(ответ)

4-6. Энергия активации некоторой реакции в 1.5 раза больше, чем энергия активации другой реакции. При нагревании от T₁ до T₂ константа скорости второй реакции увеличилась в a раз. Во сколько раз увеличилась константа скорости первой реакции при нагревании от T₁ до T₂?(ответ)

4-7. Константа скорости сложной реакции выражается через константы скорости элементарных стадий следующим образом:

Выразите энергию активации и предэкспоненциальный множитель сложной реакции через соответствующие величины, относящиеся к элементарным стадиям.(ответ)

4-8. В необратимой реакции 1-го порядка за 20 мин при 125 о С степень превращения исходного вещества составила 60%, а при 145 o C такая же степень превращения была достигнута за 5.5 мин. Найдите константы скорости и энергию активации данной реакции .(ответ)

4-9. Реакция 1-го порядка при температуре 25 о С завершается на 30% за 30 мин. При какой температуре реакция завершится на 60% за 40 мин, если энергия активации равна 30 кДж/моль?(ответ)

4-10. Реакция 1-го порядка при температуре 25 о С завершается на 70% за 15 мин. При какой температуре реакция завершится на 50% за 15 мин, если энергия активации равна 50 кДж/моль?(ответ)

4-11. Константа скорости реакции первого порядка равна 4.02 . 10 -4 с -1 при 393 К и 1.98 . 10 -3 с -1 при 413 К. Рассчитайте предэкспоненциальный множитель для этой реакции.(ответ)

4-12. Для реакции H₂ + I₂ 2HI константа скорости при температуре 683 К равна 0,0659 л/(моль. мин), а при температуре 716 К — 0,375 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 700 К.(ответ)

4-13. Для реакции 2N₂O 2N₂ + O₂ константа скорости при температуре 986 К равна 6,72 л/(моль. мин), а при температуре 1165 К — 977,0 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 1053,0 К.(ответ)

4-14. Трихлорацетат-ион в ионизирующих растворителях, содержащих H + , разлагается по уравнению

H + + CCl₃COO — CO₂ + CHCl₃

Стадией, определяющей скорость реакции, является мономолекулярный разрыв связи C- C в трихлорацетат-ионе. Реакция протекает по первому порядку, и константы скорости имеют следующие значения: k = 3.11 . 10 -4 с -1 при 90 о С, k = 7.62 . 10 -5 с -1 при 80 о С. Рассчитайте а) энергию активации, б) константу скорости при 60 о С.(ответ)

4-15. Для реакции CH₃COOC₂H₅ + NaOH ѕ CH₃COONa + C₂H₅OH константа скорости при температуре 282,6 К равна 2,307 л/(моль. мин), а при температуре 318,1 К — 21,65 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 343 К.(ответ)

4-16. Для реакции C₁₂H₂₂O₁₁ + H₂O C₆H₁₂O₆ + C₆H₁₂O₆ константа скорости при температуре 298,2 К равна 0,765 л/(моль. мин), а при температуре 328,2 К — 35,5 л/(моль. мин). Найдите энергию активации этой реакции и константу скорости при температуре 313,2 К.(ответ)

4-17. Вещество разлагается двумя параллельными путями с константами скорости k₁ и k₂. Какова разность энергий активации этих двух реакций, если при 10 o C k₁/k₂ = 10, а при 40 o C k₁/k₂ = 0.1?(ответ)

4-18. В двух реакциях одинакового порядка разница энергий активации составляет E₂ — E₁ = 40 кДж/моль. При температуре 293 К отношение констант скорости равно k₁/k₂ = 2. При какой температуре константы скорости сравняются?(ответ)

4-19. Разложение ацетондикарбоновой кислоты в водном растворе — реакция первого порядка. Измерены константы скорости этой реакции при разных температурах:

T, о С

k. 10 5 , с -1

Рассчитайте энергию активации и предэкспоненциальный множитель. Чему равен период полураспада при 25 о С? (ответ)

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Решение задач на тему: "Правило Вант-Гоффа". 1 часть. 10 класс.Скачать

Правило Вант- Гоффа. Уравнение Аррениуса.

для студентов направления 6070104 «Морской и речной транспорт»

«Эксплуатация судового электрооборудования и средств автоматики»,

направления 6.050702 «Электромеханика» специальности

«Электрические системы и комплексы транспортных средств»,

«Электромеханические системы автоматизации и электропривод»

дневной и заочной форм обучения

Тираж_____экз. Подписано к печати_____________.

Заказ №________. Объем 1,08 п.л.

Изд-во “Керченский государственный морской технологический университет”

98309 г. Керчь, Орджоникидзе, 82.

Правило Вант- Гоффа. Уравнение Аррениуса.

Согласно эмпирическому правилу Вант — Гоффа, сформулированному около 1880г., скорость большинства реакций увеличивается в 2-4 раза при повышении температуры на 10 градусов, если реакция проводится при температуре, близкой к комнатной. Например, время полуразложения газообразного оксида азота (V) при 35°С составляет около 85мин., при 45°С-около 22мин. и при 55°С — около 8мин.

Мы уже знаем, что при любой постоянной температуре скорость реакции описывается эмпирическим кинетическим уравнением, представляющим в большинстве случаев (за исключением реакции с весьма сложным механизмом) произведение константы скорости на концентрации реагентов в степенях, равных порядкам реакции. Концентрации реагентов практически не зависят от температуры, порядки, как показывает опыт,- тоже. Следовательно, за резкую зависимость скорости реакции от температуры ответственны константы скоростей. Зависимость константы скорости от температуры принято характеризовать температурным коэффициентом скорости реакции, которыйпредставляет собой отношение констант скорости при температурах, отличающихся на 10 градусов

; ; = ; =

=

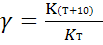
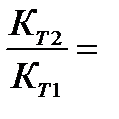
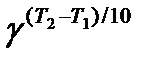
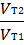
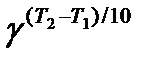
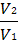
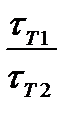
и который по правилу Вант — Гоффа равен приблизительно 2-4.

Попытаемся объяснить наблюдаемые высокие значения температурных коэффициентов скоростей реакции на примере гомогенной реакции в газовой фазе с позиций молекулярно-кинетической теории газов. Чтобы молекулы взаимодействующих газов прореагировали друг с другом, необходимо их столкновение, при котором одни связи рвутся, а другие образуются, в результате чего и появляется новая молекула — молекула продукта реакции. Следовательно, скорость реакции зависит от числа столкновений молекул реагентов, а число столкновений, в частности, — от скорости хаотического теплового движения молекул. Скорость молекул и соответственно число столкновений растут с температурой. Однако только повышение скорости молекул не объясняет столь быстрого роста скоростей реакций с температурой. Действительно, согласно молекулярно-кинетической теории газов средняя скорость молекул пропорциональна квадратному корню из абсолютной температуры, т.е, при повышении температуры системы на 10 градусов, скажем, от 300 до 310К, средняя скорость молекул возрастет лишь в 310/300 = 1,02 раза — гораздо меньше, чем требует правило Вант -Гоффа.

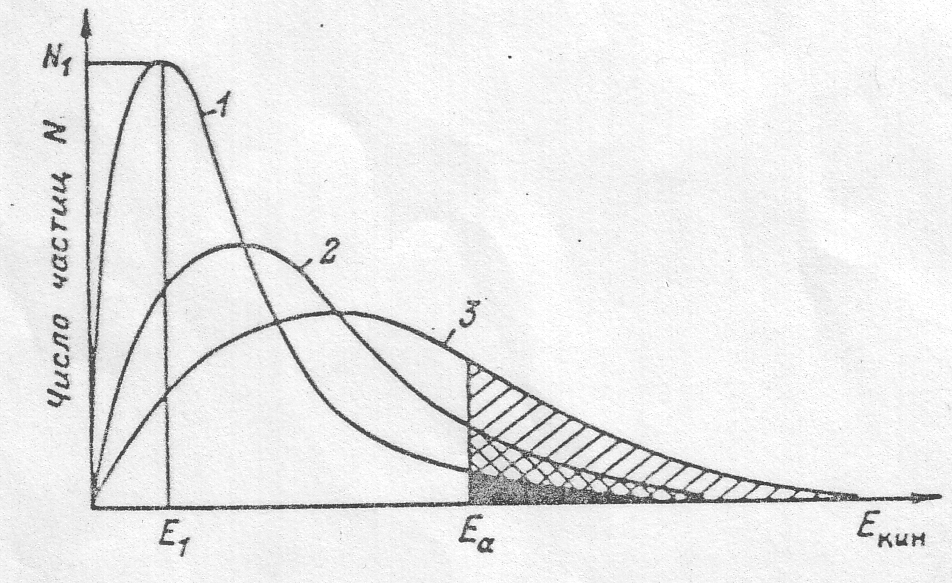
Таким образом, одним только увеличением числа столкновений нельзя объяснить зависимость констант скоростей реакции от температуры. Очевидно, здесь действует еще какой-то важный фактор. Чтобы вскрыть его, обратимся к более подробному анализу поведения большого числа частиц при различных температурах. До сих пор мы говорили о средней скорости теплового движения молекул и ее изменении с температурой, но если число частиц в системе велико, то по законам статистики отдельные частицы могут иметь скорость и соответственно киетическую энергию, в большей или меньшей степени отклоняющуюся от среднего значения для данной температуры. Эта ситуация изображена на рис. (3.2), который

показывает, как распределены части-

3.2. Распределение частиц по кинетической энергии при различных температурах:

2-Т₂; 3-Т₃; Ti / — энергия активации химической реакции с участием катализатора.

Видео:Влияние температуры на скорость химических реакций. 10 класс.Скачать

Уравнения Вант-Гоффа и Аррениуса.

Константа скорости реакции k в уравнении (2.1.3) есть функция температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Вант-Гоффом, сформулировавшим следующее эмпирическое (т.е. на основе экспериментальных данных) правило: При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.

Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент Вант-Гоффа (γ). Математически правило Вант-Гоффа можно записать следующим образом:

(2.1.17)

(2.1.18)

Правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).

Взаимодействие частиц осуществляется при их столкновениях; однако не каждое столкновение приводит к химическому взаимодействию частиц. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации. Энергия активации Е_А – необходимый избыток энергии (по сравнению со средней энергией реагирующих веществ), которым должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.

Рассмотрим путь некоторой элементарной реакции

Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:

Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер (рис.2.1.5). Энергия активации реакции равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’_А выше, нежели энергия активации прямой реакции E_A. Для эндотермической реакции наблюдается обратное соотношение между Е’_А и Е’_А. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции – тепловой эффект реакции (DU на рис 2.1.5.).

Рис. 2.1.5. Энергетический профиль химической реакции. E_исх – средняя энергия частиц исходных веществ, E_прод – средняя энергия частиц продуктов реакции.

Поскольку температура – мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции.

Зависимость константы скорости от температуры описывается уравнением Аррениуса:

(2.1.19)

Здесь A – предэкспоненциальный множитель. Из уравнения (2.1.19) нетрудно показать его физический смысл: величина А равна константе скорости реакции при температуре, стремящейся к бесконечности.

Прологарифмируем соотношение (2.1.19):

Как видно из последнего выражения, логарифм константы скорости линейно зависит от обратной температуры; величину энергии активации E_A и логарифм предэкспоненциального множителя A можно определить графически (соответственно тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат, рис.2.1.6).

Рис.2.1.6.Зависимость логарифма константы скорости химической реакции от обратной температуры.

Зная энергию активации реакции и константу скорости при какой-либо температуре T₁, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T₂:

Катализ

Скорость химической реакции при данной температуре определяется скоростью образования активированного комплекса, которая, в свою очередь, зависит от величины энергии активации. Во многих химических реакциях в структуру активированного комплекса могут входить вещества, не являющиеся реагентами по уравнению реакции; очевидно, что в этом случае изменяется и величина энергии активации процесса. В случае наличия нескольких переходных состояний реакция будет идти в основном по пути с наименьшим активационным барьером.

Катализ – явление изменения скорости химической реакции в присутствии веществ, состояние и количество которых после реакции остаются неизменными.

Различают положительный и отрицательный катализ (соответственно увеличение и уменьшение скорости реакции), хотя часто под термином «катализ» подразумевают только положительный катализ; отрицательный же катализ называют ингибированием.

Вещество, входящее в структуру активированного комплекса, но не являющееся реагентом, называется катализатором. Для всех катализаторов характерны такие общие свойства, как специфичность и селективность действия.

Специфичность катализатора заключается в его способности ускорять только одну реакцию или группу однотипных реакций и не влиять на скорость других реакций. Так, например, многие переходные металлы (платина, медь, никель, железо и т.д.) являются катализаторами для процессов гидрирования; оксид алюминия катализирует реакции гидратации и т.д.

Селективность катализатора – способность ускорять одну из возможных при данных условиях параллельных реакций. Благодаря этому можно, применяя различные катализаторы, из одних и тех же исходных веществ получать различные продукты. В следующей таблице катализаторы реакций приведены слева в скобках, а реакции, которые они ускоряют — правее:

Причиной увеличения скорости реакции при положительном катализе является уменьшение энергии активации при протекании реакции с участием катализатора (рис. 2.1.7). На этом рисунке приведено сравнение энергетических профилей реакции с катализатором и без катализатора. Катализатор снижает энергию активации и направляет реакцию по другому пути, как минимум, с образованием двух переходных состояний (соответствующих двум максимумам на энергетическом профиле реакции с катализатором). Если переходные состояния характеризуются более низкой энергией активации (Е_А,к) по сравнению с реакцией в отсутствии катализатора (Е_А), то альтернативная реакция протекает с более высокой скоростью, несмотря на образование большего числа промежуточных продуктов.

Рис.2.1.7.Сравнениеэнергетических профилей реакций без катализатора (сплошная линия) и с катализатором (пунктирная линия)

Утверждение о том, что катализатор снижает энергию активации, строго говоря, не корректно, так как реакция в присутствии катализатора не идентична исходной реакции. Это совершенно иной путь реакции, имеющий более низкий активационный барьер.

Поскольку, согласно уравнению Аррениуса (2.1.19), константа скорости химической реакции находится в экспоненциальной зависимости от величины энергии активации, уменьшение последней вызывает значительное увеличение константы скорости.

Необходимо отметить, что наличие катализатора не влияет на величину изменения термодинамического потенциала (ΔG или ΔF) в результате процесса и, следовательно, никакой катализатор не может сделать возможным самопроизвольное протекание термодинамически невозможного процесса (ΔG или ΔF которого больше нуля). Катализатор не изменяет величину константы равновесия для обратимых реакций; влияние катализатора в этом случае заключается только в ускорении достижения равновесного состояния, т.е. увеличения скоростей прямой и обратной реакций.

В зависимости от фазового состояния реагентов и катализатора, различают гомогенный и гетерогенный катализ. Гомогенный катализ – каталитические реакции, в которых реагенты и катализатор находятся в одной фазе. Наиболее распространенным типом гомогенного катализа является кислотный катализ, при котором в роли катализатора выступают ионы водорода Н + . Гетерогенный катализ – каталитические реакции, идущие на поверхности раздела фаз, образуемых катализатором и реагирующими веществами. Механизм гетерогенно-каталитических процессов значительно более сложен, чем в случае гомогенного катализа.

🎥 Видео

Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

Скорость химических реакций. 9 класс.Скачать

Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Решение задач на тему: "Правило Вант-Гоффа". 2 часть. 10 класс.Скачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

Химическая кинетика. Скорость химической реакции | ХимияСкачать

Уравнение Аррениуса, часть 1Скачать

Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать

ДВИ по химии. Термохимия. Уравнение Аррениуса, закон Гесса, задачи на теплоемкостьСкачать

124. Правило Вант-Гоффа. Решение задач.Скачать

Использование уравнения Аррениуса для решения задач (2/2). Химия для поступающих.Скачать

Химическое равновесие. Константа равновесия. 10 класс.Скачать

Порядок реакцииСкачать

С.Аррениус. Определение кислоты как вещества (видео 1) | Кислоты и Основания | ХимияСкачать

Порядок реакции и энергия активацииСкачать

Скорость реакции. Химия – ПростоСкачать