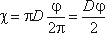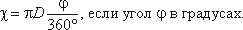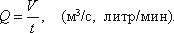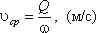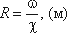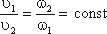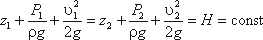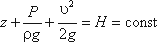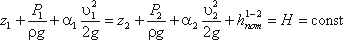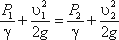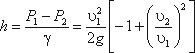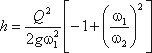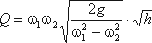Связь скорости и давления в потоке на основе уравнения бернулли

Видео:Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

Уравнение Бернулли. Связь скорости и давления в потоке. Структура формулы для силы в гидродинамике

Физические свойства и параметры жидкостей. Основные элементы потоков и виды течений. Кавитация.

Жидкостью называют физическое тело, характеризующееся свой­ством текучести, обусловленное высокой степенью подвижности частиц жидкости друг относительно друга.

Различают капельные и газообразные жидкости.

Физические свойства жидкостей:

1)Плотностью жидкости называют массу единицы объема жидкос­ти. Если объем жидкости V имеет массу М, то плотность равна p=M/V.

Плотность жидкости зависит от температуры, давления и солености, однако в большинстве случаев влиянием температуры и давления на жидкость несжимаемых жидкостей можно пренебречь.

2)Весомость жидкости характеризуется ее сдельным весом (или объемным весом). Удельным весом y называют вес единицы объема жидкости. у=G/V (кН/м 3 )

3) Вязкостью жидкости называют свойство, в силу которого в ней

проявляются силы внутреннего трения препятствующие сдвигающим

усилиям. При малых скоростях движение жидкости вблизи поверхности тела имеет ламинарный (слоистый) характер. Отдельные слои жидкос­ти движутся почти параллельными струйками без переноса конечных малых объемов жидкости из одного слоя в соседние.

При движении слоев жидкости с различными скоростями между ними возникают напряжения внутреннего трения т, значения которых согласно закону Ньютона пропорциональны градиенту скорости ди/дп по нормали п к плоскости скольжения АВ : τ=µ(dvdn)

При решении ряда теоретических вопросов в целях упрощения изучения явлений, связанных с обтеканием тел жидкостью, в (гидродинамике часто пользуются понятием идеальной жидкости. В отличие от реальной абстрактная идеальная жидкость абсолютно несжимаема и обладает абсолютной подвижностью т. е. лишена вязкости. Коэффициенты μ и v идеальной жидкости равны нулю. Одна­ко все выводы, сделанные для идеальной жидкости, корректируются или дополняются применительно к реальной жидкости.

При обтекании жидкостью твердых тел свойство вязкости проявляется наиболее полно лишь в зоне, непосредственно примыкающей к телу, называемой пограничным слоем.

В пределах пограничного слоя скорости частиц жидкости изменяются от нуля на поверхности тела до значения скорости внешней среды на границе слоя.

Виды течения жидкостей.

В гидромеханике рассматривают два основных режима течения жидкости — ламинарный и турбулентный. При ламинарном движении связь между движущимися слоями осуществляется силами молекулярного сцепления частиц. Т. о., ламинарное движение жидкости характеризуется струйным течением, при котором отдельные ее слои движутся с различными скоростями в плоскостях, приблизительно параллельных поверхности границы потока. Сдвиг слоев сопровождается образованием касатель­ных напряжений трения, подчиняющихся закону Ньютона.

При турбулентном движении частицы жидкости помимо главного направления перемещаются в поперечном направлении. Следовательно, при турбу­лентном движении перенос количества движения из одного слоя в другой осуществляется главным образом путем перехода отдельных объемов жидкости из слоя в слой.

Линия тока- это линия, касательная к векторам скорости каждой из рассматриваемых частиц, полученная в конкретный момент времени.

Трубка тока(элементарная струйка) – часть потока однородной жидкости, проходящая через бесконечно малую площадку с одинаковыми скоростями линий тока. Основным свойством трубки тока является невозможность выхода частиц жидкости за стенки трубки тока.

Кавитация. Из уравнения Бернулли следует, что с увеличением скорости должно падать давление. При достаточно больших скоростях потока давление в точках, где коэффициент давления имеет минимальное значение, может упасть до давления насыщенных паров p_d при котором жидкость начнет кипеть. Это явление вскипания жидкос­ти без ее нагрева называют в гидромеханике кавитацией. Появлению кавитации способствуют растворенные в воде воздух и газы, которые выделяются при понижении давления. Пары жидкос­ти и выделившиеся из нее воздух и газы образуют полости, именуемые кавитационными кавернами.

Существует три вида кавитации: пузырчатая, пленочная и вихревая.

При пузырчатой кавитации каверны в виде отдельных пузырьков располагаются по телу разрозненными группами. По мере развития процесса отдельные пузырьки сливаются и образуют пленочную кави­тацию, при которой каверны существуют в виде тонких длинных полос. В ядрах вихрей возникает вихревая кавитация. Из-за различного рода случайных причин кавитационная каверна и, в первую очередь, ее задняя кромка неустойчивы и пульсируют. Если при замыкании каверны на теле часть каверны в результате пуль­саций попадает в область, где р > рd, то пар в этом месте конденсирует­ся, что происходит практически мгновенно и сопровождается звуко­вым импульсом и гидравлическими ударами. Этот процесс называется захлопыванием (замыканием) пузырьков каверны. При замыкании каждого пузырька внутри него в течение миллисекунд и даже микро­секунд возникают высокие давления. Вследствие малой площади сечения пузырьков и высоких давлений импульсного характера в ма­териале тела возникают ^напряжения, во много раз превосходящие его предел текучести. Происходит выкол материала, появляются трещины, интенсифицируется процесс коррозии. Такое разрушение материала называют кавитационной эрозией.

Из сказанного следует, что кавитация на телах (крыльях, лопастях гребных винтов) нежелательна. Для отдаления момента начала кави­тации следует по возможности увеличивать заглубление тела, подни­мая тем самым давление на поверхности тела, либо уменьшать пики разрежения £. Для уменьшения £ следует придавать телу более обте­каемую форму, увеличивая его длину по сравнению с шириной (тол­щиной).

Уравнение Бернулли. Связь скорости и давления в потоке. Структура формулы для силы в гидродинамике.

Выражением закона сохранения энергии в гидромеханике является уравнение Бернулли, связывающее между собой давление, скорость и характе­ристики жидкости. Будем считать, что жидкость идеальна и несжимаема, ее движение носит установившийся характер, а из массовых сил действует только вес. Выделим в элементарной струйке объем жидкости, образованный сечениями 1 и 2 (рис. 4.6). В течение малого промежутка времени δt этот объем переместится в положение 1′-2′, причем сечение 1 пере­двинется на расстояние δl₁ = υ₁δt а сечение 2 — на расстояние δl₂ = υ₂δt. Из уравнения неразрывности следует, что расход жидкости через любое сечение струйки должен быть одинаков, поэтому объем жидкости 1-1′ должен быть равен объему 2-2′. Обозначив этот объем через б V, получим

где ω₁ и ω₂ — площади сечений 1 и 2.

В результате получаем: z + p/γ + υ 2 /(2g) = const.

Это уравнение показывает, что сумма высоты положения сечения z пьезометрического запора p/γ и скоростного напора υ 2 /(2g) является постоянной величиной для всех сечений данной элементарной струйки. В гидромеханике используют также другую форму уравнения Бернулли:

γz + p + ρυ 2 /2 = const.

Первый член этого уравнения выражает удельную (отнесенную к еди­нице веса) потенциальную энергию сил тяжести (энергию положения), второй — удельную потенциальную энергию давления и третий -удельную кинетическую энергию. Таким образом, удельная механи­ческая энергия на всем пути движения жидкости в элементарной струйке остается постоянной, но при переходе к другой струйке ее значение может измениться.

При рассмотрении реальной жидкости в уравнении Бернулли вводят поправки на преодоление сил сопротивления, но физическая сущность уравнения и выражаемого им закона сохранения энергии и взаимозависимости скорости потока и давления в нем остается неизменной.

Коэффициент давления и его свойства. Рассмотрим обтекание симметричного профиля (например, ватерлинии судна, крыла или лопасти гребного винта) потоком безграничной жидкости, имеющим скорость υ₀ . Остановимся на двух точках одной и той же линии тока, идущей из бесконечности по оси симметрии и разветвляю­щейся в носовой критической точке. Первая точка А находится далеко перед телом в невозмущенном потоке, где скорость равна υ₀, давление р₀ ; а вторая точка В — в произвольном месте на теле, где скорость о, давление р. Так как обе точки располагаются на одной линии тока, можно связать между собой скорости и давления в этих «точках с по­мощью уравнения Бернулли :

Здесь z-Zq. Представив левую и правую части уравнения в без­размерном виде и разделив его на ρυ₀ 2 /2, получим

Левую часть этого выражения называют коэффициентом давления и обозначают р. Величина р-р₀, находящаяся в числителе, характери­зует избыточное давление (по сравнению с давлением в набегающем невозмущенном потоке). Величину ρυ₀ 2 /2, стоящую в знаменателе, называют скоростным напором. Таким образом,

Использование р‾ для характеристики давления удобно потому, что его значение, во-первых, не зависит от рода жидкости и, во-вторых, не зависит от скорости набегающего потока, являясь лишь функцией формы тела, которая определяет соотношение υ/ υ₀. Полученные вы­воды относятся, строго’ говоря, к невязкой жидкости, однако они остаются практически верными и для движения хорошо обтекаемых тел в реальной вязкой жидкости.

Структура формулы для силы в гидродинамике:

R=ξ(ρV 2 /2)Ω

Видео:Закон БернуллиСкачать

Закон Бернулли для чайников и учёных

Предисловием можно считать «За что физики не любят математиков»: http://proza.ru/2015/11/16/160

а началом — «О прилипании предметов к телу человека»: http://proza.ru/2015/03/06/306

«Наука должна быть весёлая, увлекательная и простая. Таковыми же должны быть и учёные» (П.Л. Капица). и преподаватели. Но более всего наука должна быть честная. И «Ни один человек не должен покидать стены наших университетов без понимания того, как мало он знает» (Роберт Оппенгеймер). и как мало знают учёные. А чтобы так оно и было, нужно срезать профессора математической лженауки на первой же лекции. И прежним занудой он уже не будет. Знаю, что говорю, и привожу очередной пример.

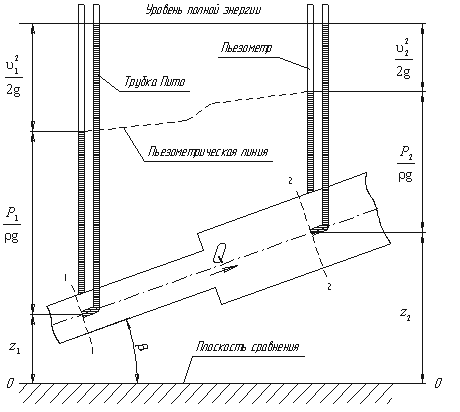
Курс лекций по гидродинамике и аэродинамике начинается с закона Бернулли. Первый вопрос профессору на засыпку: «Что именно измеряют или показывают три трубчатых манометра на картинке вверху — давление в потоках или давление потоков?».

Правильный ответ: неподвижные поверхностные манометры на картинке вверху показывают давление потоков, так как для измерения давления в потоках нужны такие манометры или датчики давления, которые находились бы внутри потоков и двигались вместе с ними. Давление внутри потоков, знаете ли, почти всегда статично. Но таких мобильных манометров, которые могли бы быть неподвижными относительно ламинарных потоков, нет в опытах к теме «Закон Бернулли». Однако вывод сделан такой, словно они есть, словно давление внутри потоков уже измерено. «Для физика должно существовать только то, что измерено» (Нильс Бор). а не то, что можно подумать, придумать, недодумать и сосчитать. Сосчитать то, чего нет, может каждый.

С маленькой лжи, как правило, начинается ложь большая. «Ложь большая» — это теория. Правильных теорий не бывает, поэтому «Никаким количеством экспериментов нельзя доказать теорию, но достаточно одного эксперимента, чтобы её опровергнуть» (А.Э.). Вся научная гидродинамика и аэродинамика опровергаются опытами по измерению давления в потоках.

Профессор, ау-у. Вы нас слышите. В опытах к теме «Закон Бернулли» нет соответствующих выводам измерений. Вы врёте по причине того, что ни один математик не отличает «давление потока» от «давление в потоке». Доказательства — картинки из учебников и глупые формулки под ними.

Так как давление в потоках у теоретиков не измерено, профессору опыт на картинке вверху говорит одно, а нам — другое: «Давление потока на параллельную потоку поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока; а давление потока на поперечную или наклонную поверхность всегда тем больше давления в потоке, чем больше скорость самого потока». И чем наш вывод хуже.

А тем-то он и хуже, что никакой научности и сложности для понимания в нём нет. К тому же, давление потока на поперечную поверхность или «скоростной напор» измеряется с помощью Г-образной «трубки Пито», вставляемой в поток загнутым концом навстречу потоку. Отсюда: давление в самом потоке примерно равно среднему арифметическому от показаний «трубки Пито» и «трубки у Бернулли». Более того, в ньютоновской механике уменьшение силы давления на параллельную потоку или телу поверхность с увеличением скорости потока или тела и одновременное увеличение давления потока или тела на поперечную поверхность можно объяснить простым векторным разложением силы давления потока или тела. Чем больше скорость автомобиля, тем меньше его вес и давление на дорожное полотно; чем больше скорость потока, тем меньше его давление на стенки трубы. Пусть пока будет так.

Конечно, наши выводы профессору будут сильно не по нутру. Но если он будет ещё в состоянии что-то говорить и продолжит настаивать на том, что «С увеличением скорости потока давление внутри потока уменьшается», то срежем его вторым вопросом: «Почему причина и следствие в формулировке общепризнанного закона Бернулли переставлены местами?».

Действительно, так сформулировать общий закон потоков мог только теоретик с математическим складом ума, для которого «Что полумёртвый равен полуживому, что полуживой равен полумёртвому, а «полу-» вообще можно сократить». А для физика и инженера давление всегда первично, а сам поток и его скорость — это всегда лишь следствие. Инженер так никогда не скажет: мол, чем больше скорость потока, тем меньше давление в нём. Для него это утверждение является противоречием здравому смыслу, то есть оксюмороном: дескать, чем выше фонтан, тем меньше давление в трубе. А как скажет инженер?

Инженер скажет: «Поток можно создать двумя противоположными, но равнозначными способами — локальным (или местным) повышением давления и локальным понижением его, потому что любой поток всегда движется в сторону меньшего давления. Это главный закон потоков или аксиома потоков, поэтому давление в потоке всегда стремится к выравниванию с внешним давлением и к уменьшению. При этом чем значительнее перепад и падение давления мы имеем или создаём, тем больше будет и скорость потока».

Можно короче: «Чем больше падение давления в потоке или на данном участке трубы, тем больше здесь и скорость самого потока». И это будет тривиальный закон потоков, у которого уже есть все пять обязательных признаков новой истины: простота, ясность, универсальность, «предсказательная сила» и антинаучность. Опровергнуть этот закон сможет только тот, кто создаст поток жидкости или газа, движущийся из области пониженного давления в область повышенного давления, то есть против действия превосходящих сил давления и упругости. Шутка.

«Тривиальный» — значит, яснее и проще некуда; значит, это закон-аксиома. К примеру, очень значительный перепад давления мы имеем сразу за камерой сгорания ракеты (примерно 250 атмосфер), и только поэтому скорость частиц реактивной струи, как говорят, достигает 3-х км/с. Вопрос профессору: «Что толкает ракету — закон сохранения импульса или асимметричное давление непрерывного взрыва в асимметричной камере сгорания?». Если скажет, что закон, перед вами математик. Стреляйтесь сразу, ибо ничто физическое и реально существующее вы ему объяснить уже не сможете (никто не сможет). «Математики похожи на французов: что бы вы ни сказали, они всё переведут на свой собственный язык. Получится нечто противоположное» (Гёте).

Если скоростной поток жидкости инженеры создают в длинной горизонтальной трубе постоянного сечения, то тут будет так: чем большее давление нагнетается в трубе, тем больше будет скорость потока в трубе при постепенном падении давления в потоке к концу трубы, то есть к расширителю потока. Всё проще простого: наибольшее давление в потоке будет в начале трубы, а наименьшее — в конце, при этом скорость несжимаемого потока будет одинаковой и там, и тут. Постепенное падение давления в потоке будет происходить по причине уменьшения массы (как меры инерции) и веса прокачиваемых жидкостей или газов на различных участках протяжённой трубы по мере приближения к концу трубы.

Любой пожарник скажет, что так оно и есть, ведь давление воды и в вертикальном потоке тоже убывает по мере приближения к концу пожарного рукава по причине уменьшения веса воды в столбе воды. А физик вспомнит ещё и про третий закон Ньютона — «Действие не может быть больше противодействия». «Действие» — это в данном случае сила нагнетаемого давления; а «противодействие» — это масса и вес потока плюс атмосферное давление на противоположном конце трубы. Противодействие уменьшается к концу трубы, и давление в потоке стремится к атмосферному.

Итак, давление в потоке жидкости на разных участках трубопровода всегда различное, а скорость потока всегда одна и та же; давление в жидкости может уменьшаться, а скорость потока при этом может сохраняться. Где тут закон Бернулли для давления в потоках. Законы Ньютона, да, мал-мало есть, а Бернулли нет и близко. Но для математиков закон есть закон, поэтому давление в скоростном потоке у них всегда низкое по всей длине трубопровода. Трубопровод разорвало. и никто не знает почему. А виноват Даниил Бернулли. Но «Кто ж его посадит, он же — па-мят-ник!».

Инженер-аэродинамист сформулирует свой закон потоков примерно так: «Давление потока на параллельную или отрицательно наклонную поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока или поверхности (верхней поверхности крыла); а давление потока на поперечную или положительно наклонную поверхность всегда тем больше давления в самом потоке, чем больше скорость потока или поверхности (нижней поверхности атакующего крыла)». И это будет качественный закон взаимодействия потоков с поверхностями, так как в каждом конкретном случае величина давления потока на поверхность зависит не только от скорости потока, но и от физических свойств потока и поверхности, поэтому она не вычисляется, а только измеряется. Следовательно, математикам и в аэродинамике делать особо нечего.

Так что, два математических закона Бернулли мы отменили. Зато, теперь имеем два основных физических закона потоков — тривиальный и качественный. И всё в этих законах понятно, и всё работает. Профессор «падсталом». Но добьём его математическую лженауку.

Действие этих двух законов во многих опытах и явлениях складывается или накладывается, поэтому наблюдаемый результат нельзя объяснять действием только какого-то одного закона. Но объединённого закона Бернулли или третьего математического закона потоков никогда не было, поэтому как определить «личную долю» каждого закона в результате того или иного опыта к теме «Закон Бернулли» не знает ни один математик. но знает каждый инженер. Он просто измеряет с помощью манометров и динамометров давление в потоке и давление потока при различной скорости потока, а потом лишь сравнивает результаты измерений. и никаких теорий потоков для него словно не существует. Действительно, зачем вычислять, если можно измерить.

Сосчитать то, чего нет, может каждый. и превратить теоретическую физику в то, чего не может быть, чего уже никто не понимает, — тоже. Математические законы Бернулли — это лишь частный случай того, чего не может быть. Впрочем, математик всегда начинает считать, не спев подумать. Сейчас мы в этом снова убедимся.

Если подуть между двумя бумажными листами, подвешенными параллельно друг другу, листы сблизятся и почти сомкнутся. Можно подуть, а можно, наоборот, прососать пылесосом воздух между листами — результат тот же.

Математик Леонард Эйлер назвал этот опыт своего друга Даниила Бернулли «Великим парадоксом», ведь в первом случае листы должны были раздвинуться расширяющимся сжатым потоком. Сам назвал — сам и объяснил. через постоянство суммы потенциальной и кинетической или полной энергии замкнутой системы. Объяснил опять же уменьшение давления в потоке с увеличением скорости потока, а не уменьшение давления потока на листы, то есть объяснил совсем не то, что надо было объяснять. И объяснил опять же математикам, а не инженерам. Инженеры твёрдо знают: давление в потоке выдуваемого из лёгких воздуха не может быть меньше атмосферного давления. А вот давление выдуваемого потока на параллельные листы может быть меньше атмосферного, поэтому листы и смыкаются. Так мы о том и говорим. Кстати, ещё вопросец на засыпку: «С какого места в опытах к теме «Закон Бернулли» начинается «замкнутая система?». Профессор, ау-у. (Правильный ответ: «С головы».)

Качественный закон потоков гласит: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». Можно короче: «Давление потока на параллельную поверхность всегда тем меньше, чем больше хаос в движении частиц потока».

В этой формулировке уже появилась физическая, а не математическая или теоретическая причина уменьшения давления потока на поверхность — это хаос или беспорядок в движении пограничных частиц потока. Вот почему на результат действия первого или тривиального закона потоков всегда накладывается действие второго или качественного закона, если мы рассматриваем взаимодействие потоков со стенками трубы, например, или с подвешенными листами. Однако давление внутри потока по-прежнему не измерено, а хаос в пограничном слое потока увидеть нельзя… Нет, уже всё можно. Человек, знаете ли, видит мир не глазами и слышит его не ушами.

В гидродинамике давление всегда первично, а скорость потока вторична; в аэродинамике скорость крыла всегда первична, а давление неподвижной атмосферы на него всегда вторично. Плоское крыло самолёта или птицы не изменяет давление в неподвижной атмосфере, а изменяется с увеличением скорости и угла атаки лишь взаимодействие быстрого крыла с атмосферой. Но в наших рассуждениях крыло чаще всего неподвижно, а это атмосфера «набегает» на крыло, словно всё происходит в аэродинамической трубе или в статическом (стационарном) потоке. Просто так нам удобнее рассуждать и объяснять.

У инженеров всё, что летает, делает это по причине совсем небольшой положительной разницы или асимметрии атмосферного давления на крыло. Появление подъёмной силы как раз и обусловлено качественным законом потоков: «Давление атмосферного потока на верхнюю отрицательно наклонную поверхность быстрого крыла тем меньше давления в самой атмосфере, чем больше хаос и разрежение частиц воздуха над ней; а давление потока на нижнюю положительно наклонную поверхность крыла тем больше атмосферного давления, чем больше скорость крыла, его угол наклона или атаки и деформация или уплотнение упругого воздуха под быстрым крылом». Как диагональ делит прямоугольник на два равных треугольника, так и плоское атакующее крыло делит набегающий поток на две самостоятельные и равнозначные причины возникновения подъёмной силы.

Вспомним, атмосферное давление на уровне моря равно 1,0033 кг/см2. Это очень большая сила, которая давит на неподвижное плоское крыло совершенно одинаково и сверху, и снизу. Если атмосферное давление со стороны одной из поверхностей крыла убрать, то со стороны противоположной поверхности тут же возникнет сила равная 10033 кг/м2. Да, 10 тонн на каждый квадратный метр крыла! И что мы имеем: орёл весом 4 кг, имея площадь «несущих поверхностей» как раз 1м2, почти неподвижно парит в вышине при положительной разнице атмосферных давлений на его крылья всего 0,04% от теоретически возможного 1 кг/см2; АН-2 («кукурузник») летает горизонтально на разности 0,4% атмосферного давления; а скоростному современному пассажирскому авиалайнеру для горизонтального полёта достаточно и 5% от 1 кг/см2 или 50 г/см2.

Как инженеры это узнали? Они применили принцип пропорциональности Леонардо да Винчи и разделили вес орла или летательного аппарата на площадь его несущих поверхностей. Вот и всё. А у математиков всё, что летает, летать не может по причине крайне не достаточной (в 6 раз меньше веса самолёта или божьей твари) подъёмной силы, вычисленной ими по самым надёжным математическим законам ньютоновской механики. Можете посмотреть по запросу «Парадокс шмеля», как математики из NASA и британские учёные вычисляли подъёмную силу. Ужас! Знание математической физики сделало их ещё глупее, чем когда они родились. И вообще, математик, считающий себя физиком, — это ноль в квадрате. Считать, что подъёмная сила крыла есть результат сопротивления воздушной среды его движению, в наше время может только профессор математики, а не физики. Читайте по запросу «О математическом идеализме в физике» (это не только мои статьи).

Идеальный или самый эффективный аэродинамический профиль – это «беспрофиль», то есть плоское, как лезвие безопасной бритвы, крыло. И это для передовых инженеров уже аксиома или «новая аэродинамика», а Природа это знала ещё со времён первых летающих насекомых и птеродактилей. Так вот, асимметричное атмосферное давление на совершенно плоское крыло возникает и при его нулевом угле наклона к вектору движения набегающего атмосферного потока, если верхняя поверхность крыла испещрена микроскопическими неровностями, а нижняя – максимально гладкая. В воде «эффект хаоса над крылом» проявляется ещё значительно сильнее.

Это утверждение доказано самой эволюцией живой природы и передовой практикой авиастроения. Смотрим на расправленное крыло любой птицы: сверху оно бархатистое и может играть всеми цветами радуги, что физику говорит о дисперсии света на мельчайших неровностях на поверхности, а снизу – всегда очень плотное, гладкое и со стальным отливом. Смотрим на современный пассажирский «Боинг»: сверху он словно матовый, а снизу – зеркально гладкий. И пусть та положительная разница в атмосферном давлении на крыло, которая возникает только по причине различного качества покрытия его аэродинамических поверхностей, будет и недостаточной для полёта, но именно она и позволит самолёту или птице лететь горизонтально с меньшим углом атаки, то есть с меньшим лобовым сопротивлением, экономя топливо и силы.

Инженеры «Боинга» говорят, что уже экономят на «эффекте хаоса над крылом» до 7-ми процентов топлива, а это огромные деньги. Смотрите фотографии «Боингов» и читайте по запросу «Аэродинамика Боинг». А наши дурни из Сколково одной краской покрывают весь Боинг. Смотрите по запросу «Красим Боинг». Кожа акулы тоже только кажется гладкой, а на ощупь она сравнима с наждачной бумагой. Шершавая кожа способствует образованию хаоса в пограничном слое воды, что ещё больше уменьшает её давление на быструю акулу. И таких примеров «мильён».

«Если ты не можешь объяснить что-либо просто — значит, ты сам этого не понимаешь» (Эйнштейн). или говоришь о том, чего нет, ибо познанное всегда проще непознанного. «Вашу теорию относительности не понимает никто в мире, но Вы всё-таки стали великим человеком» (Чаплин). «Человек, на исправление ошибок которого потребовалось целое десятилетие, — это действительно человек» (Оппенгеймер). Эйнштейн очень много сделал для любителей огромных и сверхмалых чисел и всевозможных формул, но он «наследил» ещё и в аэродинамике.

В рассуждениях Эйнштейна о подъёмной силе («Элементарная теория полёта и волн на воде» 1916. Берлин) есть только верхняя горбатая поверхность крыла и есть закон Бернулли: мол, крыло делит набегающий поток на два потока, из которых верхний, огибающий горб, всегда несколько быстрее прямого нижнего, а раз быстрее, то и меньше давление в нём; дескать, вот вам и положительная или подъёмная разница атмосферного давления на крыло. Но при этом его ни разу не посетила простая мысль вот о чём: при увеличении скорости крыла разница в скорости верхнего и нижнего потока остаётся той же самой, то есть 1/9 — 1/6; закон Бернулли действует и над, и под крылом. и как итог: при увеличении скорости самолёта подъёмная сила по закону Бернулли увеличиваться не может, то есть самолёт на горизонтальных крыльях просто-напросто не взлетит. Однако небольшая подъёмная сила горизонтального горбатого крыла всё же имеет место быть, но не по закону Бернулли, а по причине разрежения и завихрения воздуха за горбом, то есть по качественному закону потоков (отрицательно наклонная поверхность).

Как авторитетные авиаторы ни пытались хоть что-то объяснить знаменитому теоретику про угол атаки крыла и наклон всего самолёта к вектору движения, как о главной причине возникновения положительной разницы атмосферного давления, он лишь снисходительно посмеивался над ними (к примеру, переписка Эйнштейна с испытателем самолётов Паулем Георгом Эрхардтом). Дундуковость учёного всегда начинается с непонимания, незнания или с «незамечания» им сущей простоты и с желания выглядеть умным. Смотрите «Эйнштейн и подъёмная сила, или Зачем змею хвост». «Математика — единственный совершенный метод водить себя за нос» (Эйнштейн). и других — тоже. Вопросы профессору на засыпку: «Почему в рассуждениях теоретиков горбатого профиля закон Бернулли действует только над крылом?»; «Что доказал лейтенант Кульнев, совершивший в 1913 году затяжной горизонтальный полёт на перевернутом гидросамолете?» (Он доказал, что с хорошим движком и дверь полетит — был бы положительный угол атаки.)

Про математика Николая Жуковского и про его «присоединённые вихри», как о причине возникновения подъёмной силы, толкающей крыло снизу вверх, даже упоминать не хочется. Самолёты Эйнштейна и Жуковского — «беременная утка» и «шестикрылый монстр доаэродинамического периода» — не полетели по причине большого паразитного лобового сопротивления очень горбатых крыльев. Но именно они, а не Природа являются основоположниками и «отцами» аэродинамики. А ведь ещё Галилей завещал нам искать подсказки для ответов на все вопросы у Природы и в лабораториях, а не в научных текстах. Смотрите по запросу «Посмеёмся, мой Кеплер, великой глупости людской». «Великая глупость людская» — это глупость учёных. А их, учёных и учителей, и во времена Галилея было, мягко говоря, не мало.

Повторяем только что доказанный вывод: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». «Степень хаоса» не вычисляется по математическим формулам, а «личная доля» каждого из двух законов потоков в наблюдаемых эффектах уменьшения давления потоков на поверхности с увеличением их скорости в каждом конкретном случае зависит от качества потоков и поверхностей, поэтому при желании тоже только измеряется, но не вычисляется. Вот почему математикам уже делать больше нечего — ни в аэродинамике, ни в объяснениях взаимодействий потоков с поверхностями. Так что, не только «Математика убивает креативность» (Андрей Фурсенко), но и креативность убивает математику. Причём математика убивает креативность всегда, а креативность убивает математику ещё недостаточно часто. «Занимаясь расчётами, ты попадаешь впросак, прежде чем успеваешь это осознать» (Эйнштейн). но чаще этого не замечаешь.

Однако вторым законом потоков объясняются не только опыты к теме «Закон Бернулли», но ещё один раз доказывается нечто совсем другое, позволяющее увидеть истоки математического идеализма в физике и похоронить математическую физику, как науку о природе. «Законы математики, имеющие какое-либо отношение к реальному миру, ненадёжны; а надёжные математические законы не имеют отношения к реальному миру» (А. Эйнштейн). Сейчас мы эту словесную формулу математического идеализма просто-напросто докажем. Вернее, я докажу, а вы. согласитесь.

Невесомые вещества – это хаосы: «Если нет веса у беспорядочно мечущейся частицы, то нет его и у целого» (Левкипп и Демокрит). Древние греки считали воздух невесомым веществом, но даже не все плазмы – это невесомые хаосы: «неорганизованная» плазма – это всем хаосам хаос; а «самоорганизованная» плазма — совсем не хаос. Последняя образуется в замкнутых объёмах или под внешним давлением и состоит из равноудалённых колеблющихся частиц. Напряжением взаимного отталкивания равноудалённых частиц «организованная» плазма способна разорвать любые оболочки или направленным действием пробить любую броню, что и используется инженерами-взрывниками уже довольно давно. (Смотрите по запросу «Самоорганизованная плазма».)

Самый яркий пример «неорганизованной» плазмы – это удалённая от поверхности плазменная атмосфера Солнца или его корона; самый простой пример «организованной» плазмы — пламя свечи, обжатое атмосферным давлением. Но у хаосов нет не только ни веса, ни существенного давления, но они ещё и непрозрачны ни для звука, ни для электромагнитных колебаний. К примеру, «неорганизованная» плазма, окружающая гиперзвуковую ракету, не позволяет управлять ракетой с помощью радиосигналов.

«Все жидкости и газы на Земле имеют вес и находятся под давлением веса собственных и выше расположенных слоёв» (Архимед). Поэтому все прозрачные жидкости и газы состоят из примерно одинаковых, равноудалённых и условно неподвижных (колеблющихся или дрожащих) частиц, находящихся в состоянии взаимного отталкивания и относительного (или чуткого) равновесия и взаимно отталкивающихся в газах на расстояниях много больших, чем в жидкостях. Отсюда: давление в любой точке водоёма или атмосферы равно напряжению взаимного отталкивания равноудалённых частиц в этой точке, и по силе оно равно весу всех частиц над этой точкой. Уберите атмосферное давление, и капля воды тут же исчезнет, разлетевшись на молекулы, а аквариум с водой словно взорвётся. И повинно в том будет как раз-таки «напряжение взаимного отталкивания равноудалённых частиц». Смотрите по запросу «Современный Архимед. Трактат «О плавающих телах» и «К физике антигравитонов». Там есть опыты, позволяющие буквально увидеть неподвижность колеблющихся частиц в жидкостях и в газах. Особенно показателен опыт по мгновенному замерзании переохлаждённой воды при её встряхивании в пластиковой бутылке. Многие его знают, но не понимают.

Способность атомов и молекул к движению взаимного отталкивания пропорциональна температуре. А температура – это «опосредованное мерило» интенсивности атомных и внутриатомных движений и величины гравитационных моментов (квантов, импульсов) атомов, передающихся от атома к атому путём индукции.

Гравитационные моменты у более возбуждённых атомов больше, а у «менее горячих» — меньше. Этими моментами атомы словно дёргают друг друга, понуждая сами себя к взаимному отталкиванию, к синхронности движений и к равновесию. Так осуществляется встречный индукционный или индуктивный теплообмен в природе и в гравитационной физике. О квантовой природе тяготения и отталкивания, электромагнетизма и прочего всего смотрите по запросу «Гравитационная физика. Атом».

Или вы думаете, что теоретики знают об атоме больше инженеров. Отнюдь. «Нет ни малейших признаков того, что атомная энергия когда-нибудь станет доступна людям. Это значило бы, что человек научился расщеплять атом» (Альберт Эйнштейн). «Десять лет моей жизни было потрачено только на то, чтобы полностью избавиться от идей этого человека» (Роберт Оппенгеймер об Эйнштейне и его теориях). Роберт Оппенгеймер — это инженер-изобретатель, «папа атомной бомбы». Он же на вопрос президента Гарри Трумэна «Когда русские смогут сделать атомную бомбу?» ответил: «Никогда». Дескать, в учебниках русских нет и намёка на реальную физику атома. И был абсолютно прав: русские сделали американскую атомную бомбу. Но в наших учебниках ничто не изменилось, словно атомного взрыва и не было. Смотрите по запросу «Гравитационная физика. Атом».

Теперь, думаю, вам уже более понятно — почему с увеличением скорости потока его давление на параллельную поверхность всегда уменьшается. Да, потому что при движении жидкого или газообразного кристалла вдоль шершавой поверхности возникает невесомый беспорядок в движении частиц пограничного слоя этого кристалла. Однако всё, что человек понимает, он когда-то понял сам — даже если ему в этом кто-то помог.

P.S. «Учёные объясняют то, что уже есть; инженеры создают то, чего никогда не было. И всё понятно, и всё работает. Мы же соединяем теорию с практикой: ничто не работает. и никто не знает почему» (Эйнштейн). У теоретиков ничто не работает потому, что у них «самая успешная математическая теория 20-го века» — это кинетическая теория теплоты и давления, не имеющая к физической реальности никакого отношения. Да и вся математическая или теоретическая физика — это то, чего не может быть. А то, что может быть, это — инженерная физика, то есть физика природных и искусственных технологий. И вообще, наука — это логичная совокупность всех явлений и всего известного опыта, а также поиск нового опыта. «Логичная» — значит, простая, явная, последовательная, взаимосвязанная и взаимообусловленная реальность, имеющая общую причинность.

Там, где нет науки, есть научность. Научность появляется именно там, где посредством математических действий и преобразований доказывается возможность невозможного, где одно непонятное объясняется посредством чего-то ещё более непонятного, где кому-то удаётся из очевидного сделать невероятное и где постулируется, то есть берётся за основу, то, что невозможно ни опровергнуть, ни доказать. Это словно злонамеренно рассчитано на то, что глупцам умным и научным кажется лишь то, чего они не понимают. «Конечно, ваша гипотеза безумна. Но достаточно ли она безумна. Если гипотеза недостаточно безумна, науке от неё не будет никакого толку» (Нильс Бор). а учёным — проку.

Простые и разумные идеи нужны только инженерам. И только они знают, что сложных открытий не бывает, что простота ближе к Природе и к пониманию Природы. но истинная простота — это как раз то, что впервые даётся познанию людей труднее всего. Но простота — это ещё и то, что учёным труднее всего объяснить. Более того, простота объяснения того или иного явления или опыта — это для теоретика хуже воровства и большое свинство. Дошло уже то того, что сказать правду учёным может только хам, антисемит и неуч. И только поэтому самым большим парадоксом является то, что этот мир всё же познаваемый (с).

И ещё. Всем теоретикам и преподавателям на засыпку: «Какой теорией руководствовались братья Райт, когда делали свой воздушный винт, который у них получился с КПД 78-80%, если научной аэродинамики ещё не было, а КПД самых современных пропеллеров из дерева не превышает 85%?».

Хотелось бы услышать возражения или замечания, но их почему-то нет. Видимо, с тем, что мы живём в эпоху математических лженаук, уже никто не спорит.

Воображеньем прозорливым
К догадкам верным нас несло…
Но сонм учёных кропотливых
Свернул наш поиск — на число.

И лязгом счёта оглушённый
Забыл наш ум — решенья ключ…
Стал слепнуть, в шоры цифр втеснённый.
А был так зряч и так могуч!

Уж цифре памятник построен,
Распята Истина на нём.
Поклонник счёта, жрец и воин
Простёрся ниц перед числом:

Не осознать бедняге в заблужденье,
Как много лжи за ширмой исчисленья!

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Связь скорости и давления в потоке на основе уравнения бернулли

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

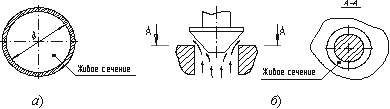
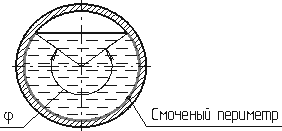
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы — круг (рис.3.1, б); живое сечение клапана — кольцо с изменяющимся внутренним диаметром (рис.3.1, б).

Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

Для круглой трубы

если угол в радианах, или

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

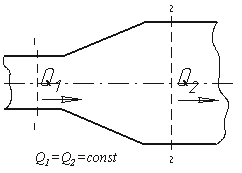
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

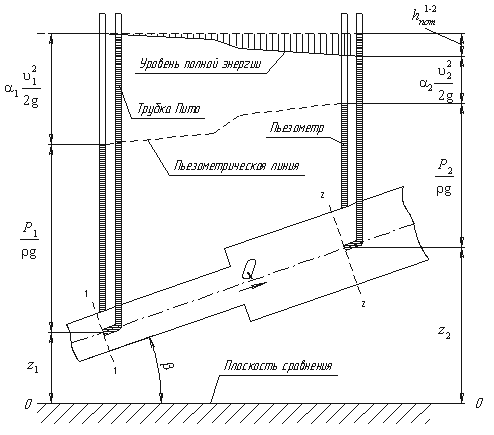
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 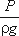. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;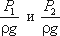
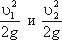
— удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
— удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

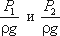
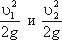
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; — пьезометрические высоты; — скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

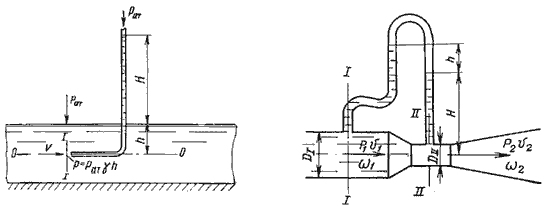
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н — столб жидкости в трубке Пито.

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

Выражение, стоящее перед 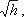, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Видео:Трубка Пито и скоростной напорСкачать

Основы гидравлики

Видео:Парадокс сужающейся трубыСкачать

Уравнение Бернулли — фундамент гидродинамики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

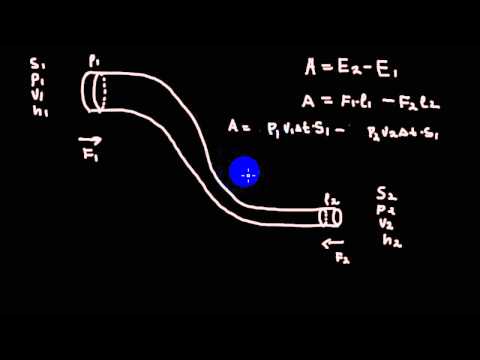
Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

По закону сохранения энергии, изменение полной энергии E₂ — E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ — на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = — p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ — плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ — площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .

🎬 Видео

Уравнение Бернулли гидравликаСкачать

Уравнение Бернулли для потока жидкостиСкачать

Закон БернуллиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Закон Бернулли и движение по инерцииСкачать

Подъёмная сила крыла ● 1Скачать

Уравнение БернуллиСкачать

Уравнение БернуллиСкачать

Дистанционная работа 5 - иллюстрация уравнения БернуллиСкачать

Существует ли динамическое давление?Скачать

Основы гидродинамики и аэродинамики | уравнение БернуллиСкачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Гидродинамика. Уравнение Бернулли. Физика 10 классСкачать