Свойства модулей в неравенствах и уравнениях

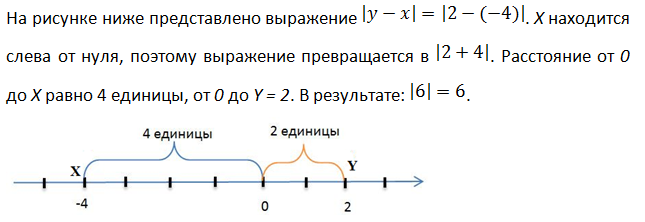
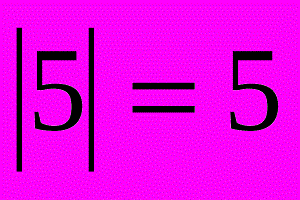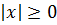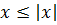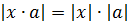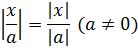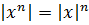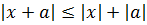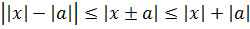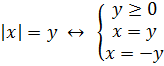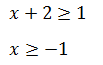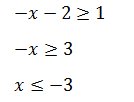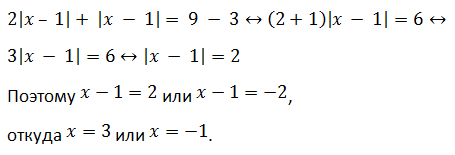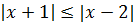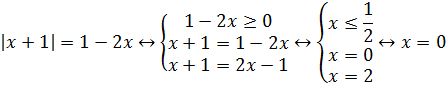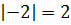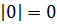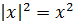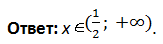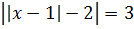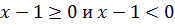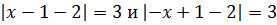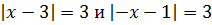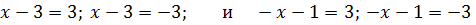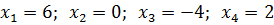В этой статье введем и очень подробно разберем такое важное понятие, как модуль числа. Разберемся, откуда модуль взялся, какими свойствами обладает. Научимся решать уравнения и неравенства с модулем.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

«Величина» числа

Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.

Геометрический смысл

Представьте, что вы стоите в точке 0 на числовой оси. Слева от вас, в точке − 1 0 0 , находится школа. Справа, в точке 5 0 , находится ваш дом. Математически число − 1 0 0 меньше, чем 5 0 . Но вот идти до школы 1 0 0 метров влево гораздо дольше, чем пройти 5 0 метров до дома вправо. В этом смысле «величина» пройденного расстояния в − 1 0 0 метров больше, чем 5 0 метров.

Пусть теперь школа находится в точке − 1 0 , а дом в точке 1 0 . Математически вновь получаем, что − 1 0 меньше 1 0 . Но вот нам, находящимся в 0 , совершенно нет разницы: идти − 1 0 метров влево или 1 0 метров вправо. В обоих случаях мы пройдем 1 0 метров. То есть, по «величине» числа − 1 0 и 1 0 равны.

Количественный смысл

Рассмотрим числа 5 0 и − 1 0 0 . В математическом смысле − 1 0 0 гораздо меньше 5 0 . А давайте посмотрим на эти числа под другим углом. У вас есть всего 5 0 рублей и вы задолжали другу. Ваш долг составляет − 1 0 0 рублей. В этом смысле «величина» вашего долга в − 1 0 0 рублей гораздо больше имеющихся у вас 5 0 рублей. Получается, что математически − 1 0 0 меньше 5 0 , но по «величине» − 1 0 0 больше 5 0 .

Теперь рассмотрим числа − 1 0 и 1 0 . Математически, опять же, − 1 0 меньше 1 0 . Но, пользуясь нашей аналогией с долгом, своими 1 0 рублями вы полностью покроете долг в − 1 0 рублей. То есть, по «величине» число − 1 0 равно числу 1 0 .

Понятие величины

Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.

Видео:Неравенства с модулем | Математика | TutorOnlineСкачать

Модуль числа

Сформулируем на строгом языке математики наше интуитивное представление о «величине» числа, которое мы сформировали в предыдущем разделе.

Модуль или абсолютная величина вещественного числа x — само число x , если оно неотрицательно, иначе − x .

Допустим, мы хотим найти модуль какого-то числа a . Согласно определению, нам надо провести элементарную проверку. Если число a положительное или равно 0 , то модулем a и является само a . Если же a меньше 0 , то результатом модуля будет − a .

∣ 5 ∣ = 5 ∣ 0 ∣ = 0 ∣ − 1 2 ∣ = − ( − 1 2 ) = 1 2

Легко убедиться, что модуль числа полностью соответсвует по смыслу «величине» числа, рассмотренной в предыдущем разделе. Там мы утверждали, что по «величине» − 1 0 0 больше 5 0 , а − 1 0 равно 1 0 . И действительно:

∣ − 1 0 0 ∣ = 1 0 0 ∣ − 1 0 ∣ = 1 0 ​ ∣ 5 0 ∣ = 5 0 ∣ − 1 0 0 ∣ > ∣ 5 0 ∣ ∣ 1 0 ∣ = 1 0 ∣ − 1 0 ∣ = ∣ 1 0 ∣ ​

Положение знака нестрогого неравенства в определении модуля не имеет значения:

Обозначим второе определение модуля числа x как ∣ x ∣ ′ . Покажем, что какой x не возьми, будет выполняться ∣ x ∣ = ∣ x ∣ ′ .

Пусть x > 0 . По классическому определению ∣ x ∣ = x . По второму: ∣ x ∣ ′ = x . То есть ∣ x ∣ = ∣ x ∣ ′ .

Пусть x = 0 . По классическому определению ∣ 0 ∣ = 0 . А вот во втором определении 0 попадает уже под второе условие, то есть ∣ 0 ∣ ′ = − 0 = 0 . Опять имеем ∣ 0 ∣ = ∣ 0 ∣ ′ .

Наконец, пусть x 0 . По классическому определению ∣ x ∣ = − x . У второго определения та же ситуация: ∣ x ∣ ′ = − x . Получается, что и в этом случае ∣ x ∣ = ∣ x ∣ ′ .

Итак, мы рассмотрели все возможные значения для x и во всех случаях ∣ x ∣ = ∣ x ∣ ′ . Это и означает, что между двумя определениями нет никакой разницы ■

Такое определение иногда бывает полезно. Например, если x лежит в следующих пределах: − 1 0 ≤ x ≤ 0 , то можно сразу сказать, что ∣ x ∣ = − x , даже несмотря на то, что для x = 0 так выражаться будет некорректно, ведь ∣ 0 ∣ = 0 , а не − 0 .

Видео:МодульСкачать

Свойства модуля

У модуля есть очень много полезных свойств, которые сильно помогают при решении уравнений, неравенств, доказательстве теорем и так далее. Рассмотрим самые полезные из них. Все свойства ниже формулируем для любых вещественных чисел x и y .

Очевидные свойства

Наиболее очевидные свойства модуля напрямую вытекают из рассмотренного ранее понятия о «величине» числа. Например, мы определили «величину» числа как само число с «отброшенным» знаком. Это означает, что «величина» не может быть отрицательной.

Видео:11 класс, 29 урок, Уравнения и неравенства с модулямиСкачать

Модуль числа знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Видео:Контрольная работа. Уравнения с МОДУЛЕМСкачать

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Видео:Модуль в математике. Уравнения и неравенства | Математика ЕГЭ | УмскулСкачать

Свойства модуля

Важно помнить о следующих свойствах:

1. Правило раскрытия: абсолютная величина любого числа больше или равна нулю:
2. Если абсолютные значения содержат выражения противоположных значений, они равны:
3. Значение числа не превышает величину его модуля:
4. Правило раскрытия при произведении:
5. Правило, применимое при делении:
6. При возведении в степень:
7. Сумма величин:
8. Двойной модуль:

Видео:МОДУЛЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Модуль комплексного числа

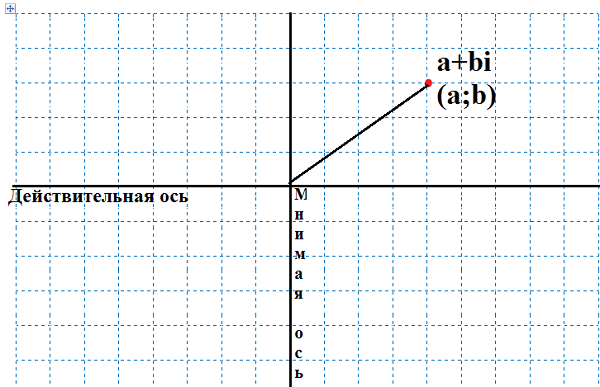
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Видео:НЕРАВЕНСТВА С МОДУЛЕМСкачать

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Видео:Как решать неравенства с модулем. Два модуля в неравенстве.Скачать

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.

Разделим интервал на 2 части:

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке .

Ответ: x = 0.

Видео:Неравенства с модулем. Как правильно раскрывать модульСкачать

Модуль суммы

Видео:Неравенства с модулем Часть 1 из 2 Простейшие неравенстваСкачать

Модуль разности

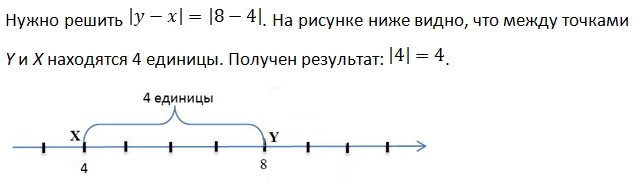
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

Видео:6 класс, 24 урок, Модульные уравнения и неравенства с одной переменнойСкачать

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Видео:Уравнения с модулемСкачать

Модуль нуля

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Видео:Уравнение с модулемСкачать

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Видео:Решение неравенства методом интерваловСкачать

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

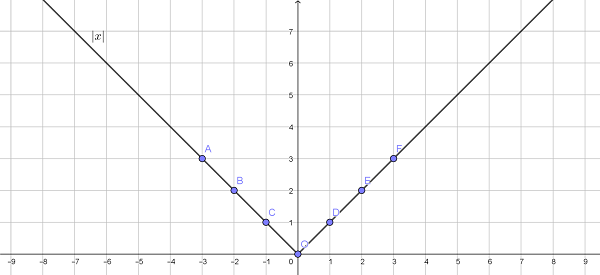
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

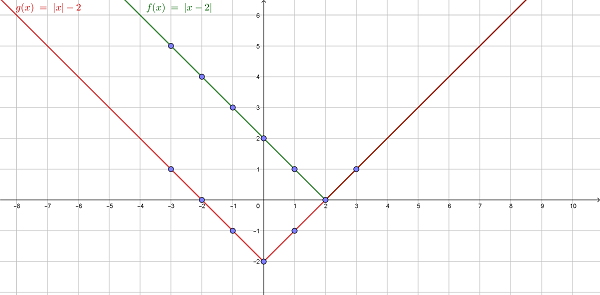
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Видео:Как решать уравнения и неравенства с модулем. Выпуск 1.Скачать

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

1. Приравнять каждое выражение к нулю.
2. Найти значения переменных.
3. Нанести на числовую прямую точки, полученные в пункте 2.
4. Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
5. Решить неравенства с полученными знаками.

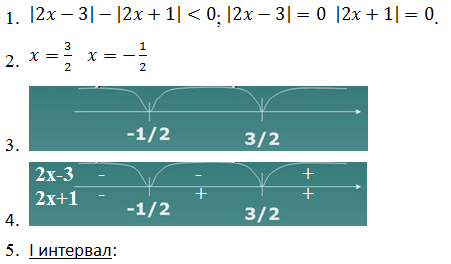
Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Видео:УРАВНЕНИЯ С МОДУЛЕМ | метод интерваловСкачать

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

• когда положительное число находится внутри модуля, достаточно просто избавиться от него,
• если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
• если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Уравнения с модулем

Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.

Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним, что

Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)

Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Слева модуль, справа число

Это самый простой случай. Решим уравнение

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:

Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.

Переменная как под модулем, так и вне модуля

Здесь приходится раскрывать модуль по определению. . . или соображать!

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения

Стало быть, годятся лишь и .

Ответ:

Квадратные уравнения с заменой |x| = t

Поскольку , удобно сделать замену |x| = t. Получаем:

Модуль равен модулю

Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:

Остаётся решить каждое из уравнений совокупности и записать ответ.

Два или несколько модулей

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Модуль в модуле

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Читайте также о том, как решать неравенства с модулем.