Свойства множества решений однородной системы линейных уравнений

Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Свойства систем линейных однородных уравнений

Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.

Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.

Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Структура общего решения системы уравнений

Однородная система линейных уравнений

всегда совместна, так как имеет тривиальное решение . Если ранг матрицы системы равен количеству неизвестных , то тривиальное решение единственное. Предположим, что . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица однородной системы при элементарных преобразованиях строк приводится к упрощенному виду , т.е. . Поэтому из (5.11) получаем общее решение однородной системы уравнений :

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Свойства решений однородной системы уравнений

1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.

В самом деле, из равенств следует, что

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность линейно независимых решений однородной системы называется фундаментальной системой (совокупностью) решений .

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец

при любых значениях произвольных постоянных также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец

Найдем ранг этой матрицы. Так как первые столбцов линейно независимы, то . Так как каждый из столбцов матрицы является решением системы , то по первой формуле из (5.13) получаем

Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, , так как после вычеркивания в матрице будет всего строк. Таким образом, . Значит, есть базисный минор матрицы , который расположен в первых ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа , что

Итак, обратное утверждение доказано.

Видео:Неоднородная система линейных уравненийСкачать

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг матрицы системы равен числу неизвестных , то система имеет единственное тривиальное решение и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

Решение. 1. Составляем расширенную матрицу системы

2-4. Используя элементарные преобразования над строками матрицы , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

Пункт 3 метода Гаусса пропускаем.

5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы

6. Находим фундаментальную систему решений. Так как и , надо подобрать линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

В результате получили фундаментальную систему решений

7. Записываем общее решение однородной системы по формуле (5.14):

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, и . Тогда получим другую фундаментальную систему решений

Несмотря на различия, обе формулы задают одно и то же множество решений.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств и следует, что .

2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

1. Используя фундаментальную матрицу однородной системы , решение неоднородной системы можно представить в виде

2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

Переменные — базисные, а — свободные.

6. Полагая , получаем частное решение неоднородной системы .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

8. Записываем по формуле (5.15) общее решение неоднородной системы

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом , используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

Записываем частное решение неоднородной системы

и составляем фундаментальную матрицу:

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

Видео:Фундаментальная система решений для однородной системы линейных уравненийСкачать

Однородные СЛАУ. Фундаментальная система решений

Видео:Решение системы уравнений методом ГауссаСкачать

Однородные СЛАУ

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в матричном виде, $A X=Theta$ всегда совместна, так как $X=Theta$ всегда является ее решением.

Заметим, что если $x_, x_$ — это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=lambda_ x_+lambda_ x_$$ $$A Y=Aleft(lambda_ x_+lambda_ x_right)=lambda_ A x_+lambda_ A x_=lambda_ Theta+lambda_ Theta=Theta$$

Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю.

Задание. Выяснить, имеет ли однородная СЛАУ $left<begin 3 x-2 y=-1 \ x+3 y=7 endright.$ ненулевые решения.

$$Delta=left|begin 3 & -2 \ 1 & 3 endright|=9-(-2)=9+2=11 neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Задание. Найти общее решение и ФСР однородной системы $left<begin x_+x_-3 x_-x_=0 \ x_-x_+2 x_-x_=0 \ 4 x_-2 x_+6 x_+3 x_-4 x_=0 \ 2 x_+4 x_-2 x_+4 x_-7 x_=0 endright.$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=left(begin 1 & 1 & 0 & -3 & -1 \ 1 & -2 & 2 & -1 & 0 \ 4 & -2 & 6 & 3 & -4 \ 2 & 4 & -2 & 4 & -7 endright)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & -6 & 6 & 15 & 0 \ 0 & 2 & -2 & 10 & -5 endright)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 9 & -3 \ 0 & 0 & 0 & 12 & -4 endright)$$

От четвертой строки отнимем $frac$ третьей и третью строку умножим на $frac$ :

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 \ 0 & 0 & 0 & 0 & 0 endright)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 endright)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A simleft(begin 1 & 1 & 0 & -6 & 0 \ 0 & -2 & 2 & 5 & 0 \ 0 & 0 & 0 & 3 & -1 endright)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_, x_$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_, x_, x_$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

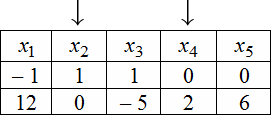
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_=1$ , $x_=0$ получаем, что $left<begin x_=-1+6 cdot 0=-1 \ x_=1-frac cdot 0=1 \ x_=3 cdot 0=0 endright.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_=0$ , $x_=2$, будем иметь, что <x_=12, x_=-5, x_=6> , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_=left(begin -1 \ 1 \ 1 \ 0 \ 0 endright), X_=left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_ X_+C_ X_=C_left(begin -1 \ 1 \ 1 \ 0 \ 0 endright)+C_left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

где коэффициенты $C_, C_$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_, C_$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

🔍 Видео

§41 Решение систем линейных однородных уравненийСкачать

Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение неоднородных линейных систем. ТемаСкачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Решение однородных линейных систем. ТемаСкачать

ФСР системы линейных уравнений. Алгоритм ГауссаСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

14. Метод Гаусса решения систем линейных уравнений ( бесконечное множество решений ). Часть 3Скачать