Данная статья представляет собой совокупность детальной информации, которая касается темы свойства корней. Рассматривая тему, мы начнем со свойств , изучим все формулировки и приведем доказательства. Для закрепления темы мы рассмотрим свойства n -ой степени.
- Свойства корней
- Свойства корня n-ой степени
- Что такое квадратный корень
- Что такое квадратный корень
- Разница между квадратным корнем и арифметическим квадратным уравнением
- Запись иррациональных чисел с помощью квадратного корня
- Извлечение корней
- Свойства арифметического квадратного корня
- Умножение арифметических корней
- Деление арифметических корней
- Возведение арифметических корней в степень
- Внесение множителя под знак корня
- Вынесение множителя из-под знака корня
- Сравнение квадратных корней
- Извлечение квадратного корня из большого числа
- Свойства корней
- Определение корня
- Арифметический корень
- Алгебраический корень
- Примеры с решением №1
- Извлечение квадратного корня из чисел
- Примеры с решением №2
- Примеры с решением №3
- 💡 Видео
Видео:Свойства корней, которые надо знатьСкачать

Свойства корней
Мы поговорим о свойствах .
- Свойство умноженных чисел a и b , которое представляется как равенство a · b = a · b . Его можно представить в виде множителей, положительных или равных нулю a 1 , a 2 , … , a k как a 1 · a 2 · … · a k = a 1 · a 2 · … · a k ;
- из частного a : b = a : b , a ≥ 0 , b > 0 , он также может записываться в таком виде a b = a b ;
- Свойство из степени числа a с четным показателем a 2 · m = a m при любом числе a , например, свойство из квадрата числа a 2 = a .
В любом из представленных уравнений можно поменять части до и после знака тире местами, например, равенство a · b = a · b трансформируется как a · b = a · b . Свойства для равенства часто используются для упрощения сложных уравнений.
Доказательство первых свойств основано на определении квадратного корня и свойствах степеней с натуральным показателем. Чтобы обосновать третье свойство, необходимо обратиться к определению модуля числа.
Первым делом, необходимо доказать свойства квадратного корня a · b = a · b . Согласно определению , необходимо рассмотреть, что a · b — число, положительное или равное нулю, которое будет равно a · b при возведении в квадрат. Значение выражения a · b положительно или равно нулю как произведение неотрицательных чисел. Свойство степени умноженных чисел позволяет представить равенство в виде ( a · b ) 2 = a 2 · b 2 . По определению квадратного корня a 2 = a и b 2 = b , то a · b 2 = a 2 · b 2 = a · b .
Аналогичным способом можно доказать, что из произведения k множителей a 1 , a 2 , … , a k будет равняться произведению квадратных корней из этих множителей. Действительно, a 1 · a 2 · … · a k 2 = a 1 2 · a 2 2 · … · a k 2 = a 1 · a 2 · … · a k .
Из этого равенства следует, что a 1 · a 2 · … · a k = a 1 · a 2 · … · a k .
Рассмотрим несколько примеров для закрепления темы.
3 · 5 2 5 = 3 · 5 2 5 , 4 , 2 · 13 1 2 = 4 , 2 · 13 1 2 и 2 , 7 · 4 · 12 17 · 0 , 2 ( 1 ) = 2 , 7 · 4 · 12 17 · 0 , 2 ( 1 ) .
Необходимо доказать свойство арифметического квадратного корня из частного: a : b = a : b , a ≥ 0 , b > 0 . Свойство позволяет записать равенство a : b 2 = a 2 : b 2 , а a 2 : b 2 = a : b , при этом a : b является положительным числом или равно нулю. Данное выражение и станет доказательством.
Например, 0 : 16 = 0 : 16 , 80 : 5 = 80 : 5 и 3 0 , 121 = 3 0 , 121 .
Рассмотрим свойство квадратного корня из квадрата числа. Его можно записать в виде равенства как a 2 = a Чтобы доказать данное свойство, необходимо подробно рассмотреть несколько равенств при a ≥ 0 и при a 0 .
Очевидно, что при a ≥ 0 справедливо равенство a 2 = a . При a 0 будет верно равенство a 2 = — a . На самом деле, в этом случае − a > 0 и ( − a ) 2 = a 2 . Можно сделать вывод, a 2 = a , a ≥ 0 — a , a 0 = a . Именно это и требовалось доказать.
Рассмотрим несколько примеров.
5 2 = 5 = 5 и — 0 , 36 2 = — 0 , 36 = 0 , 36 .
Доказанное свойство поможет дать обоснование a 2 · m = a m , где a – действительное, а m –натуральное число. Действительно, свойство возведения степени позволяет заменить степень a 2 · m выражением ( a m ) 2 , тогда a 2 · m = ( a m ) 2 = a m .
3 8 = 3 4 = 3 4 и ( — 8 , 3 ) 14 = — 8 , 3 7 = ( 8 , 3 ) 7 .
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Свойства корня n-ой степени
Для начала необходимо рассмотреть основные свойства корней n -ой степени:
- Свойство из произведения чисел a и b , которые положительны или равны нулю, можно выразить в качестве равенства a · b n = a n · b n , данное свойство справедливо для произведения k чисел a 1 , a 2 , … , a k как a 1 · a 2 · … · a k n = a 1 n · a 2 n · … · a k n ;
- из дробного числа обладает свойством a b n = a n b n , где a – любое действительное число, которое положительно или равно нулю, а b – положительное действительное число;
- При любом a и четных показателях n = 2 · m справедливо a 2 · m 2 · m = a , а при нечетных n = 2 · m − 1 выполняется равенство a 2 · m — 1 2 · m — 1 = a .
- Свойство извлечения из a m n = a n · m , где a – любое число, положительное или равное нулю, n и m – натуральные числа, это свойство также может быть представлено в виде . . . a n k n 2 n 1 = a n 1 · n 2 . . . · n k ;
- Для любого неотрицательного a и произвольных n и m , которые являются натуральными, также можно определить справедливое равенство a m n · m = a n ;
- Свойство степени n из степени числа a , которое положительно или равно нулю, в натуральной степени m , определяемое равенством a m n = a n m ;
- Свойство сравнения , которые обладают одинаковыми показателями: для любых положительных чисел a и b таких, что a b , выполняется неравенство a n b n ;
- Свойство сравнения , которые обладают одинаковыми числами под корнем: если m и n – натуральные числа, что m > n , тогда при 0 a 1 справедливо неравенство a m > a n , а при a > 1 выполняется a m a n .
Равенства, приведенные выше, являются справедливыми, если части до и после знака равно поменять местами. Они могут быть использованы и в таком виде. Это зачастую применяется во время упрощения или преобразовании выражений.
Доказательство приведенных выше свойств корня основывается на определении, свойствах степени и определении модуля числа. Данные свойства необходимо доказать. Но все по порядку.
- Первым делом докажем свойства корня n -ой степени из произведения a · b n = a n · b n . Для a и b , которые являются положительными или равными нулю, значение a n · b n также положительно или равно нулю, так как является следствием умножения неотрицательных чисел. Свойство произведения в натуральной степени позволяет записать равенство a n · b n n = a n n · b n n . По определению корня n -ой степени a n n = a и b n n = b , следовательно, a n · b n n = a · b . Полученное равенство – именно то, что и требовалось доказать.
Аналогично доказывается это свойство для произведения k множителей: для неотрицательных чисел a 1 , a 2 , … , a n выполняется a 1 n · a 2 n · … · a k n ≥ 0 .
Приведем примеры использования свойства корня n -ой степени из произведения: 5 · 2 1 2 7 = 5 7 · 2 1 2 7 и 8 , 3 4 · 17 , ( 21 ) 4 · 3 4 · 5 7 4 = 8 , 3 · 17 , ( 21 ) · 3 · 5 7 4 .
- Докажем свойство корня из частного a b n = a n b n . При a ≥ 0 и b > 0 выполняется условие a n b n ≥ 0 , а a n b n n = a n n b n n = a b .
8 27 3 = 8 3 27 3 и 2 , 3 10 : 2 3 10 = 2 , 3 : 2 3 10 .
- Для следующего шага необходимо доказать свойства n -ой степени из числа в степени n . Представим это в виде равенства a 2 · m 2 · m = a и a 2 · m — 1 2 · m — 1 = a для любого действительного a и натурального m . При a ≥ 0 получаем a = a и a 2 · m = a 2 · m , что доказывает равенство a 2 · m 2 · m = a , а равенство a 2 · m — 1 2 · m — 1 = a очевидно. При a 0 получаем соответственно a = — a и a 2 · m = ( — a ) 2 · m = a 2 · m . Последняя трансформация числа справедлива согласно свойству степени. Именно это доказывает равенство a 2 · m 2 · m = a , а a 2 · m — 1 2 · m — 1 = a будет справедливо, так как за нечетной степени рассматривается — c 2 · m — 1 = — c 2 · m — 1 для любого числа c , положительного или равного нулю.
Для того, чтобы закрепить полученную информацию, рассмотрим несколько примеров с использованием свойства:
7 4 4 = 7 = 7 , ( — 5 ) 12 12 = — 5 = 5 , 0 8 8 = 0 = 0 , 6 3 3 = 6 и ( — 3 , 39 ) 5 5 = — 3 , 39 .
- Докажем следующее равенство a m n = a n · m . Для этого необходимо поменять числа до знака равно и после него местами a n · m = a m n . Это будет означать верная запись . Для a , которое является положительным или равно нулю, из вида a m n является числом положительным или равным нулю. Обратимся к свойству возведения степени в степень и определению . С их помощью можно преобразовать равенства в виде a m n n · m = a m n n m = a m m = a . Этим доказано рассматриваемое свойство корня из корня.
Аналогично доказываются и другие свойства. Действительно, . . . a n k n 2 n 1 n 1 · n 2 · . . . · n k = . . . a n k n 3 n 2 n 2 · n 3 · . . . · n k = . . . a n k n 4 n 3 n 3 · n 4 · . . . · n k = . . . = a n k n k = a .
Например, 7 3 5 = 7 5 · 3 и 0 , 0009 6 = 0 , 0009 2 · 2 · 6 = 0 , 0009 24 .
- Докажем следующее свойство a m n · m = a n . Для этого необходимо показать, что a n – число, положительное или равное нулю. При возведении в степень n · m равно a m . Если число a является положительным или равным нулю, то n -ой степени из числа a является числом положительным или равным нулю При этом a n · m n = a n n m , что и требовалось доказать.
Для того, чтобы закрепить полученные знания, рассмотрим несколько примеров
- Докажем следующее свойство – свойство корня из степени вида a m n = a n m . Очевидно, что при a ≥ 0 степень a n m является неотрицательным числом. Более того, ее n -ая степень равна a m , действительно, a n m n = a n m · n = a n n m = a m . Этим и доказано рассматриваемое свойство степени.
Например, 2 3 5 3 = 2 3 3 5 .
- Необходимо доказательство, что для любых положительных чисел a и b выполнено условие a b . Рассмотрим неравенство a n b n . Воспользуемся методом от противного a n ≥ b n . Тогда, согласно свойству, о котором говорилось выше, неравенство считается верным a n n ≥ b n n , то есть, a ≥ b . Но это не соответствует условию a b . Следовательно, a n b n при a b .
Для примера приведем 12 4 15 2 3 4 .
- Рассмотрим свойство корня n -ой степени. Необходимо для начала рассмотреть первую часть неравенства. При m > n и 0 a 1 справедливо a m > a n . Предположим, что a m ≤ a n . Свойства позволят упростить выражение до a n m · n ≤ a m m · n . Тогда, согласно свойствам степени с натуральным показателем, выполняется неравенство a n m · n m · n ≤ a m m · n m · n , то есть, a n ≤ a m . Полученное значение при m > n и 0 a 1 не соответствует свойствам, приведенным выше.
Таким же способом можно доказать, что при m > n и a > 1 справедливо условие a m a n .
Для того, чтобы закрепить приведенные свойства, рассмотрим несколько конкретных примеров. Рассмотрим неравенства, используя конкретные числа.
Видео:Алгебра 8 класс — Свойства Квадратного Корня, Корень числа и Действия над КорнямиСкачать

Что такое квадратный корень
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Решаем примеры на вычисление с квадратными корнями.Скачать

Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Здесь могут возникнуть резонные вопросы, почему, например, в примере x 2 = 16, x = 4 и x = -4.
Видео:СВОЙСТВА КОРНЕЙ. §16 алгебра 8 классСкачать

Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
- x 2 = 16 не равно x = √16.
Это два нетождественных друг другу выражения.
- x 2 = 16 — это квадратное уравнение.
- x = √ 16 — арифметический квадратный корень.
Из выражения x 2 = 16 следует, что:
- |x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
- Пример решен неверно
- Это квадратное уравнение.
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Видео:Все типы 8 задания ОГЭ 2022 | Свойства корнейСкачать

Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Решение следующее:
Строим график функции y = x 2 .
Отмечаем решения на графике: -√2; √2.
Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .
В таком виде ответ не записывают — нужно оставить квадратный корень.
x 2 = 2.
x = √2
x = -√2.
Видео:11 класс, 6 урок, Свойства корня n-й степениСкачать

Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
- 1. Извлеките квадратный корень: √289
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Влево — 1, вверх — 7.
- 2. Извлеките квадратный корень: √3025
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
- 3. Извлеките квадратный корень: √7396
Ищем в таблице число 7396.
Влево — 8, вверх — 6.
- 4. Извлеките корень: √9025
Ищем в таблице число 9025.
Влево — 9, вверх — 5.
- 5. Извлеките корень √1600
Ищем в таблице число 1600.
Влево — 4, вверх — 0.
Извлечением корня называется нахождение его значение.
Видео:Свойства арифметического квадратного корня. 8 класс.Скачать

Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
- Корень произведения равен произведению корней
- Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
- Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Видео:Квадратные корни. Сложение корней. 8 класс #shortsСкачать

Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
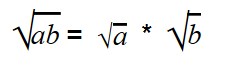 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
- Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:
Видео:Алгебра 8 класс — Квадратный Корень и его Свойства // Арифметический Квадратный КореньСкачать

Деление арифметических корней
Для деления арифметических корней используйте формулу:
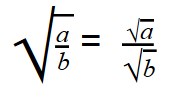 |
Примеры:
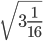
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49
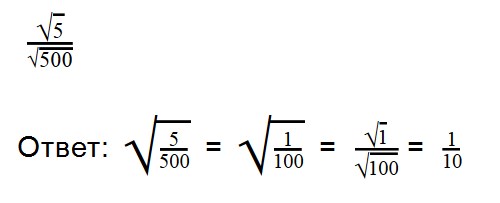
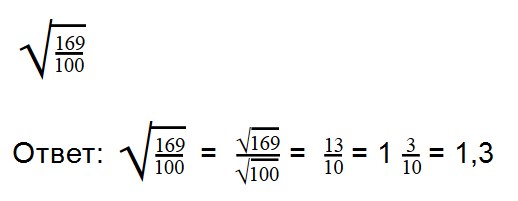
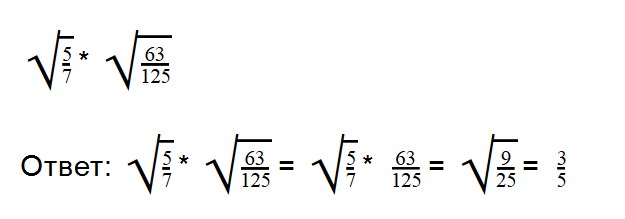
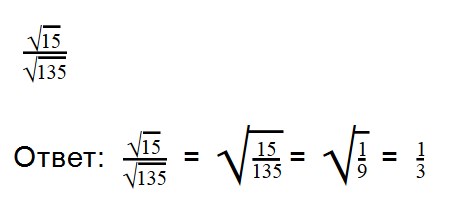
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Видео:Алгебра 8. Урок 5 - Квадратный корень и его свойстваСкачать

Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
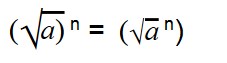 |
Примеры:
Эти две формулы нужно запомнить:
- (√a) 2 = a
- √a 2 = |a|
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Видео:Корень n-ой степени. Алгебра, 9 классСкачать

Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Дано выражение: 7√9
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Видео:Как считать корни? #shortsСкачать

Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.
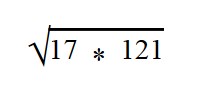
Ответ: по правилу извлечения квадратного корня из произведения,
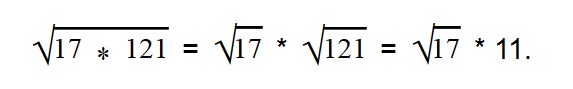
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.
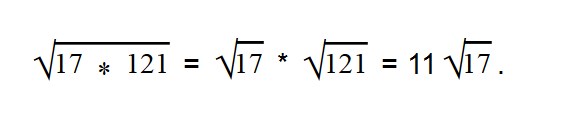
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.
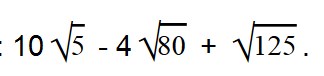
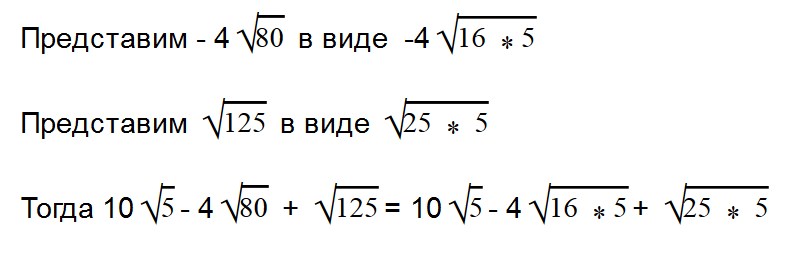
Вынесем в двух последних выражения множитель из-под знака корня.
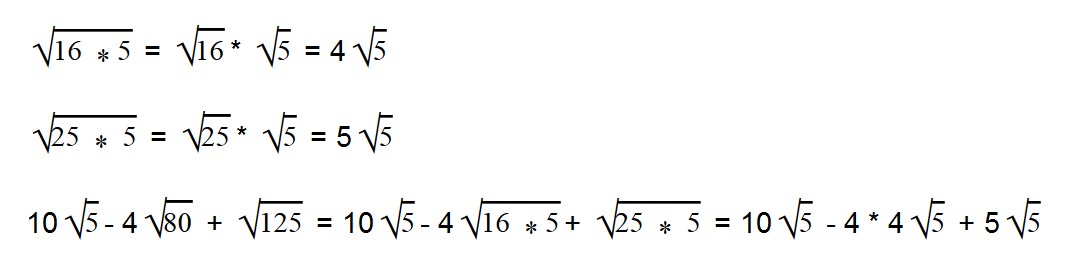
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.
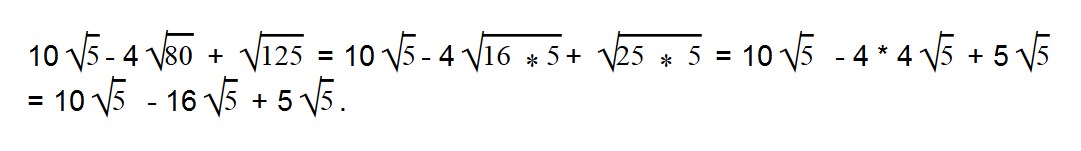
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:
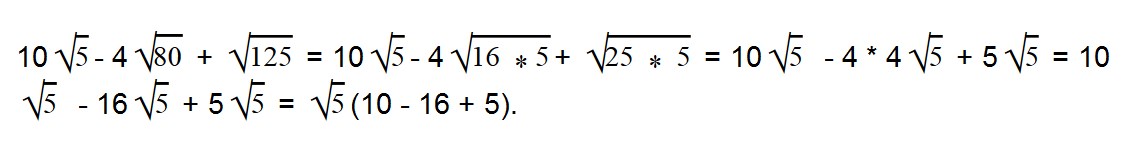
Далее вычисляем все, что в скобках:
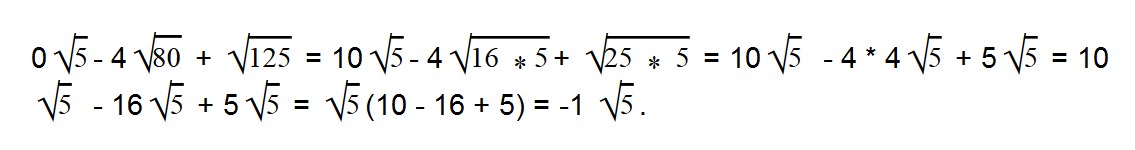
Видео:Корни для ЧайниковСкачать

Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
- Сравните два выражения: √50 и 9√5
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Это значит, что 6√5 > √18.
Сравните два выражения: 7√12 и √20
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Видео:Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 40 2 и 50 2 .
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 44 2 и 46 2 .
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- 1. Вычислите значение квадратного корня: √36
- 2. Вычислите значение квадратного корня: √64*36
- 3. Вычислите значение квадратного корня:
- 4. Вычислите значение квадратного корня:
- 5. Вычислите значение квадратного корня:
- 6. Вычислите значение выражения: 4√16 — 12
- 7. Вычислите значение выражения: 5√9 — 8
- 8. Вычислите значение выражения: 7√25 — 10
- 9. Вычислите значение квадратного корня:
- 10. Вычислите значение квадратного уравнения:
- 11. Вычислите значение квадратного уравнения:
- 12. Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем: - 13. Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9 - 14. Вычислите значение квадратного корня:
Как решаем:= 0,09
- 15. Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52. - 16. Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115. - 17. Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24. - 18. Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12. - 19. Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7. - 20. Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12. - 21. Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15. - 22. Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10. - 23. Внесите множитель под знак корня: 6√7
Как решаем: √6 2 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252. - 24. Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √8 2 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128. - 25. Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √9 2 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405. - 26. Упростите выражение: (5 — √2) 2
Как решаем: (5 — √2) 2 = 5 2 — 2 * 5 * √2 + (√2) 2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2) 2 = 27 — 10√2. - 27. Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6. - 28. Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528. - 29. Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225. - 30. Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
- 0 0 0 0 0 0
109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10
Видео:Корень n-ной степени и его свойства. Решение примеровСкачать

Свойства корней
Содержание:
Определение корня
Корнем второй степени (или квадратным) из числа 





Вообще корнем 


Число
означающее, в какой степени находится корень, называется показателем корня.
Корень обозначается знаком 
- корень кубический из 27 обозначается
- корень пятой степени из 32 обозначается
Показатель квадратного корня принято не писать вовсе; например, вместо 
Действие, посредством которого отыскивается корень, называется извлечением корня оно обратно возведению в степень, так как посредством этого действия отыскивается то, что дано при возведении (именно основание степени), а дано то, что при возведении в степень отыскивается (именно сама степень). Поэтому правильность извлечения корня мы можем всегда проверять возведением в степень. Например, чтобы проверить равенство 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Арифметический корень
Корень называется арифметическим, если он извлекается из положительного числа и сам представляет собой положительное число. Например, арифметический квадратный корень из 49 есть 7, тогда как число -7, которое тоже есть квадратный корень из нельзя назвать арифметическим.
Укажем следующие два свойства арифметического корня.
а) Пусть требуется найти арифметический 








К другому заключению мы бы пришли, если бы говорили не только о положительном значении корня; так, 
б) Возьмём каких-нибудь два неравных положительных числа, например, 49 и 64. Из того, что 49
Меньшему положительному числу соответствует и меньший арифметический корень <той же степени).
Возможно вам будут полезны данные страницы:
Алгебраический корень
Корень называется алгебраическим, если не требуется, чтобы он извлекался из положительного числа и чтобы сам он был положительный. Таким образом, если под выражением 


Укажем следующие четыре свойства алгебраического корня, а) Корень нечётной степени из положительного числа есть положительное число.
Так, 
б) Корень нечётной степени из отрицательного числа есть отрицательное число.
Так, 
в) Корень чётной степени из положительного числа имеет два значения с противоположными знаками и с одинаковой абсолютной величиной.
Так, 




Двойное значение корня обозначается обыкновенно постановкой двух знаков перед абсолютной величиной корня; так, пишут:
Чтобы в дальнейшем не оговаривать каждый раз, берём ли мы алгебраический или арифметический корень, условимся в следующем: 1) В случае чётной степени под выражением 


г) Корень чётной степени из отрицательного числа не может равняться никакому, ни положительному, ни отрицательному, числу, так как и то и другое после возведения в степень с чётным показателем даёт положительное число, а не отрицательное. Например, 
Корень чётной степени из отрицательного числа принято называть мнимым числом, остальные же числа называются вещественными, или действительными числами.
Извлечение корня из произведения, из степени и из дроби, а) Пусть надо извлечь арифметический квадратный корень из произведения 
Чтобы убедиться в верности этого равенства, возведём правую часть его в квадрат (по теореме о степени произведения):
Но согласно определению корня:
Следовательно,
Если же квадрат произведения 


Значит, чтобы извлечь арифметический корень из произведения, можно извлечь его из каждого сомножителя отдельно.
б) Легко убедиться проверкой, что следующие равенства верны.
Значит, чтобы извлечь корень из степени, показатель которой делится на показатель корня, можно разделить показатель степени на показатель корня.
в) Верны будут также и следующие равенства:
Значит, чтобы извлечь корень из дроби, можно извлечь его из числителя и знаменателя отдельно.
Напомним, что в этих правилах предполагается, что речь идёт о корнях арифметических.
Примеры с решением №1
Замечание. Если искомый корень чётной степени и предполагается алгебраическим, то перед найденным результатом надо поставить двойной знак ±.
Извлечение квадратного корня из чисел
а) Для сокращения речи в этой главе вместо «квадратный корень» будем просто говорить «корень».
б) Если возведём в квадрат числа натурального ряда: 1, 2, 3, 4, 5, . то получим такую таблицу квадратов:
1,4,9. 16, 25, 36, 49, 64, 81, 100, 121, 144, .
Очевидно, имеется очень много целых чисел, которые в этой таблице не находятся; из таких чисел, конечно, нельзя извлечь целый корень. Поэтому если требуется извлечь корень из ка-кого-нибудь целого числа, например, требуется найти 

должны найти наибольшее целое число, квадрат которого заключается в 4082 (такое число есть 63, так как 
в) Если данное число меньше 100, то корень из него находится по таблице умножения.
Извлечение корня из целого числа, меньшего 10000, но большего 100. Пусть надо найти 
десятки + единицы, и поэтому квадрат его должен равняться сумме:
Сумма эта должна быть наибольшим квадратом, заключающимся в 4082. Так как 
Тогда число десятков в корне должно быть 6. Проверим теперь, что это всегда должно быть так, т.е. всегда число десятков корня равно наибольшему целому корню из числа сотен подкоренного числа. Действительно, в нашем примере число десятков корня не может быть больше 6, так как 

А так как мы ищем наибольший целый корень, то мы не должны брать для корня 5 дес., когда и 6 дес. оказывается немного. Итак, мы нашли число десятков корня, именно 6. Пишем эту цифру направо от знака «=», запомнив, что она означает десятки корня. Возведя её в квадрат, получим 36 сотен. Вычитаем эти 36 сотен из 40 сотен подкоренного числа и к остатку приписываем число 82:
В числе 482 должна содержаться сумма:
Произведение (6 дес.) • (един.) должно составлять десятки, поэтому удвоенное произведение десятков на единицы надо искать в десятках остатка, т. е. в 48 (мы получим число их, отделив в остатке 
- В частном получим 4. Однако заранее нельзя ручаться, что цифру 4 можно принять за единицы корня, так как мы сейчас разделили на 12 всё число десятков остатка, тогда как некоторая часть из них может и не принадлежать удвоенному произведению десятков на единицы, а входить в состав квадрата единиц. Поэтому цифра 4 может оказаться велика. Надо её испытать.
Она, очевидно, будет годиться в том случае, если сумма 


Произведение 369 оказалось меньше остатка 482; значит, цифра 3 годится (если бы случилось, что и эта цифра велика, тогда надо было бы испытать следующую меньшую цифру, 2). Напишем цифру 3 в корне направо от цифры десятков. Последний остаток 113 показывает избыток данного числа над наибольшим целым квадратом, заключающимся в нём. Для проверки возведём в квадрат 63 и к результату прибавим 113:
Так как в сумме получилось данное число 4082, то действие сделано верно.
Примеры с решением №2

В примере пятом после вычитания из первой грани квадрата 8 остаток оказывается равным 0 и следующая грань тоже состоит из нулей. Это показывает, что искомый корень состоит только из 8 десятков, и потому на место единиц надо поставить нуль.
Извлечение корня из целого числа, большего 10000. Пусть требуется найти 

Теперь мы можем рассуждать совершенно так же, как и при нахождении 




Чтобы найти единицы, надо из 

Далее поступаем так, как мы поступали при нахождении 
Вообще, чтобы извлечь квадратный корень из какого угодно целого числа, надо сначала извлечь корень из числа его сотен, если это число более 100, то придётся искать корень из числа сотен этих сотен, т.е. из десятков тысяч данного числа, если и это число более 10000, придётся извлекать корень из числа сотен десятков тысяч, т.е. из миллионов данного числа, и т. д.
Примеры с решением №3
В последнем примере, найдя первую цифру и вычтя квадрат её, получаем в остатке 0. Сносим следующие 2 цифры, 51. Отделив десятки, мы получаем 5 дес., тогда как найденная удвоенная цифра корня есть 6. Значит, от деления 5 на 6 мы получаем 0. Ставим в корне 0 на втором месте и к остатку сносим следующие 2 цифры; получаем 5110. Далее продолжаем как обыкновенно.
В этом примере искомый корень состоит только из 9 сотен, и потому на месте десятков и на месте единиц надо поставить нули.
Правило. Чтобы извлечь квадратный корень из данного целого числа, разбивают его, от правой руки к левой, на грани по две цифры в каждой, кроме первой (крайней левой), в которой может быть одна цифра.
Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
Чтобы найти вторую цифру, из первой грани вычитают квадрат первой цифры корня, к остатку сносят вторую грань и число десятков получающегося числа делят на удвоенную первую цифру корня; полученное целое число подвергают испытанию.
Испытание это производится так: за вертикальной чертой (налево от остатка) пишут удвоенное ранее найденное число корня и к нему с правой стороны приписывают испытуемую цифру; получившееся после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, большее остатка, то испытуемая цифра не годится и надо испытать следующую меньшую цифру.
Следующие цифры корня находятся по тому же приёму.
Если после снесения грани число десятков получившегося числа окажется меньше делителя, т. е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
💡 Видео
Свойства Корней #математика #огэ #огэматематика #данирСкачать

Квадратный корень. 8 класс.Скачать

8 класс, 13 урок, Свойства квадратного корня. Простейшие преобразования выражений с квадратными корнСкачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать




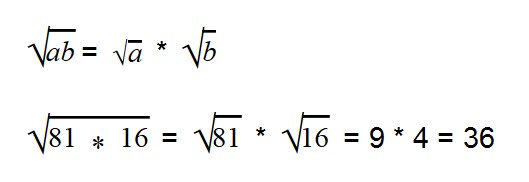
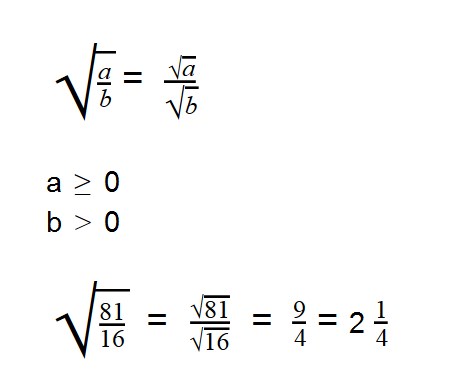
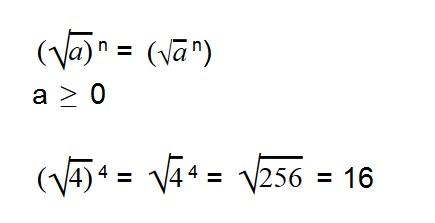
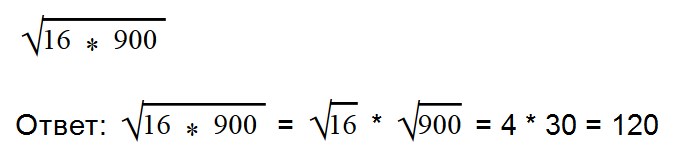
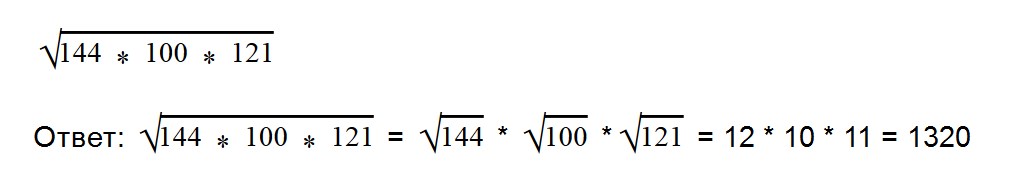

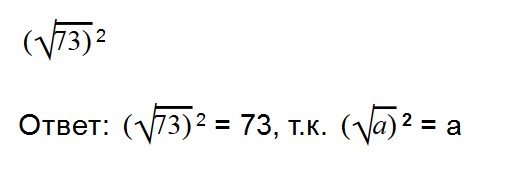
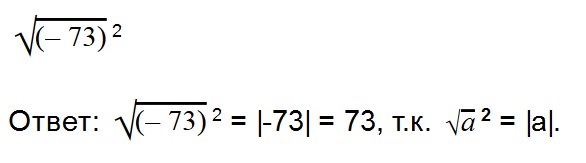
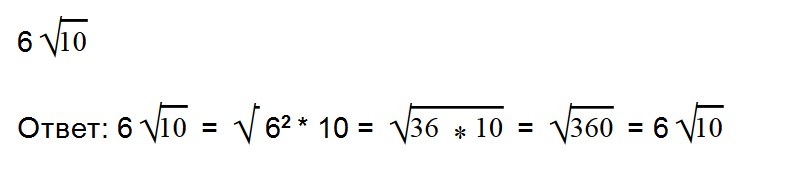
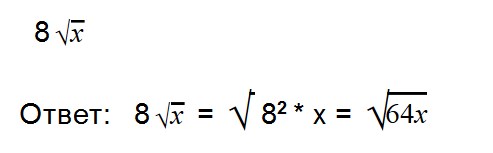
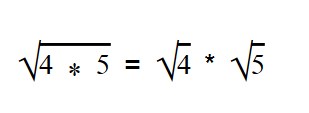
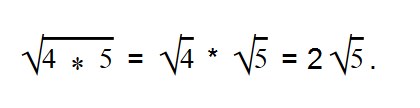
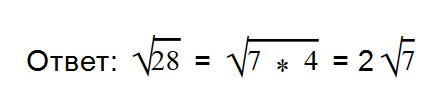
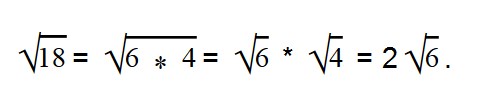


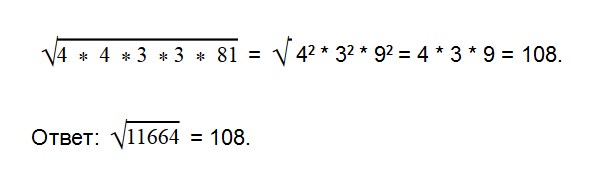

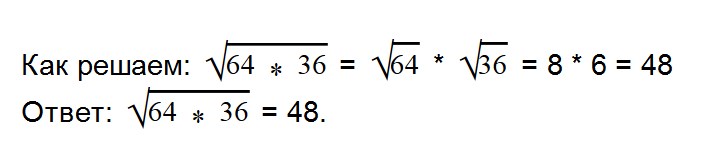
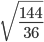
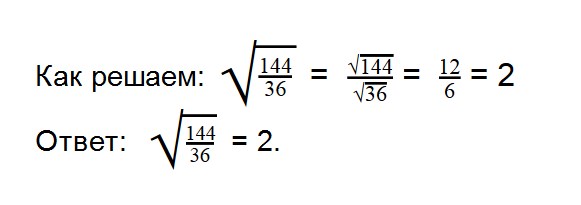
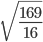
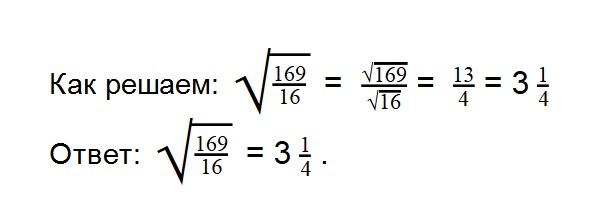
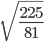
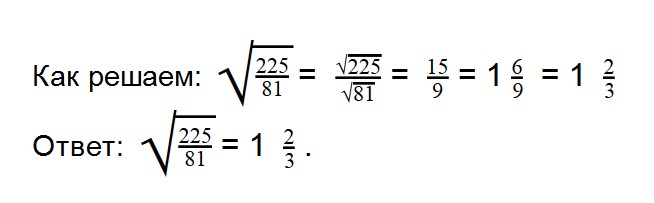
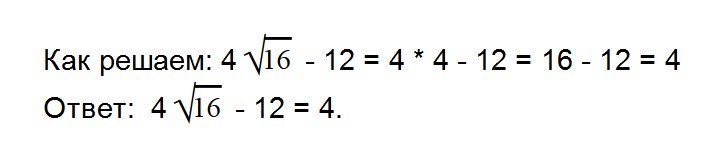
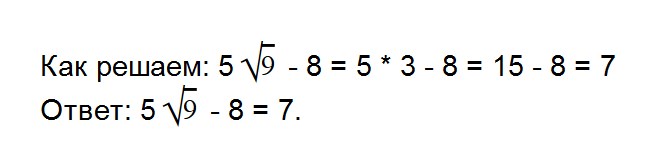
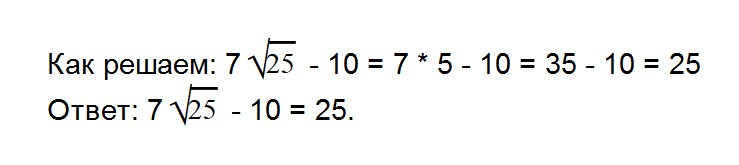
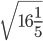
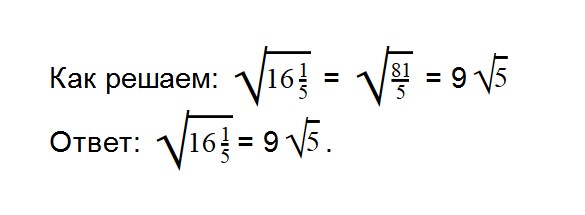

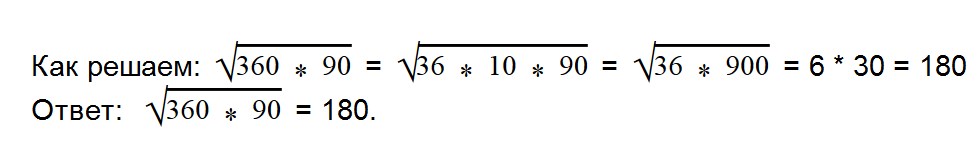

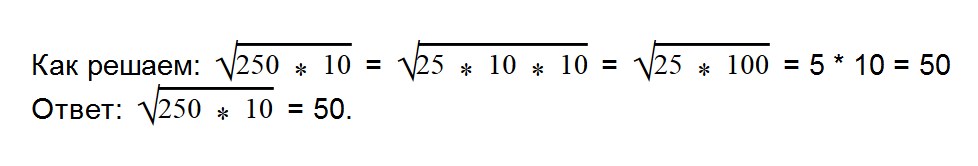
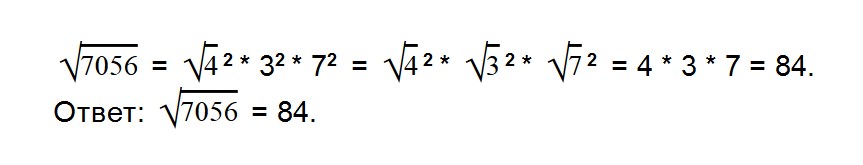
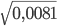









 означающее, в какой степени находится корень, называется показателем корня.
означающее, в какой степени находится корень, называется показателем корня.




























