Свойства коэффициентов в квадратном уравнении

Свойство 1. Если в уравнении ах 2 + bх +с = 0, а + b + с = 0, то один из его корней равен 1, а другой, в соответствии с теоремой Виета, равен с/а.

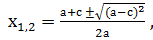
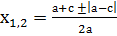
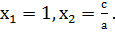
Доказательство: Имеем а+b+с=0, тогда b= — (а+с). Найдем дискриминант D=b 2 -4ас= а 2 +2ас+с 2 — 4ас = а 2 — 2ас+с 2 =(а — с) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

Пример 1: х 2 + х – 2 = 0; а = 1, в = 1, с = -2. Так как 1+1–2 =0, то х₁ =1, х₂ = -2.

Свойство 2. Если в уравнении ах 2 + bх + с = 0, а – b + с = 0 или b=a+c, то один из его корней равен –1, а другой –с/а .

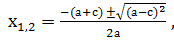
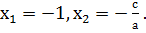
Доказательство: Имеем а — b+с=0, тогда b= а+с. Найдем дискриминант D=b 2 -4ас= а 2 +2ас+с 2 — 4ас = а 2 — 2ас+с 2 =(а — с) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

Пример 2 : х 2 – х – 2 = 0. Так как 1 – (- 1 ) + ( -2 ) = 0, то х₁ = -1, х₂ = 2.

Свойство 3. Если a = c, b = a 2 + 1, то x₁ = — a, x₂ = -1/a.

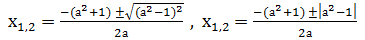
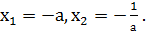
Доказательство: Имеем a = c, b = a 2 + 1. Найдем дискриминант D=b 2 -4ас= а 4 +2а 2 +1 — 4а 2 = а 4 — 2а 2 +1=(а 2 — 1) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

Пример 3. 3х 2 +10х+3=0, а=3, b=10, с=3. Так как а=с=3, b=3 2 +1=10, то х₁= -3, х₂=-1/3.

Свойство 4. Если a = c, b = -(a 2 + 1), то x₁ = a, x₂ = 1/a.

Доказательство: Имеем a = c, b = -(a 2 + 1). Найдем дискриминант D=b 2 -4ас= а 4 +2а 2 +1 — 4а 2 = а 4 — 2а 2 +1=(а 2 — 1) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

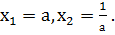
Пример 4. 3х 2 — 10х+3=0, а=3,b=-10,с=3. Так как а=с=3, b=-(3 2 +1)=-10, то х₁=3, х₂=1/3.

Приём переброски.

, первый коэффициент в качестве множителя «перебрасываем к -3», получим уравнение

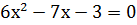
Корни 9 и -2 . Делим числа 9 и ( -2) на 6:

Ответ:

6 этап. Практическая направленность.

Задания, при решении которых необходимо умение решать квадратные уравнения.

Уровень А. 1. Найдите сумму и произведение корней уравнения: 2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны 2 и 5.

Уровень В. 2. Найдите сумму и произведение корней уравнения: 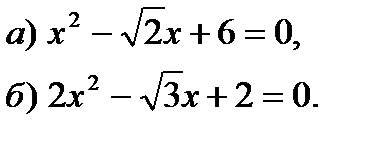2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны и .

Уровень С. Решите уравнение и выполните проверку по теореме, обратной теореме Виета: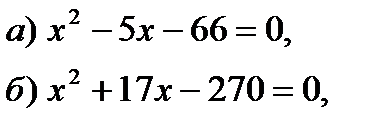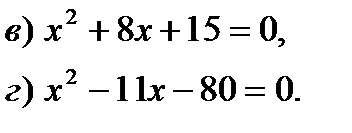

С помощью квадратных уравнений можно решать многие текстовые задачи. Вот одна из задач знаменитого индийского математика XII в. Бхаскары, решить ее можно с помощью квадратного уравнения.

На две партии разбившись, забавлялись обезьяны.

Часть восьмая их в квадрате в роще весело резвилась;

Криком радостным двенадцать воздух свежий оглашали…

Вместе сколько, ты мне скажешь, обезьян там было в роще?

1. Проводя исследование, выяснили, что кроме традиционных методов решения квадратного уравнения , которые мы узнали на уроках математики, существуют еще не менее интересные, а главные полезные свойства, практически устного решения квадратного уравнения.

2. Исследовательскую работу по математике планируем продолжать и далее.

3. Результаты своего исследования я представила в виде карточки-памятки( приложение 1) по решению квадратного уравнения.

· А.П.Ершова, В.В.Голобородько, А.С.Ершова «Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса», «ИЛЕКСА»,Москва,2003 .

· М.Б.Миндюк, Н.Г.Миндюк «Разноуровневые дидактические материалы по алгебре, 8 класс», «ГЕНЖЕР»,Москва,2002.

· «Алгебра 7-9 .Тематические зачеты»

· Г.И.Ковалева «Уроки математики в 8 классе»,издательство «БРАТЬЯ ГРИНИНЫ»,Волгоград, 2001.

Видео:Свойства коэффициентов квадратного уравненияСкачать

Урок по алгебре в 8-м классе “Свойства коэффициентов квадратного уравнения”

Разделы: Математика

Цели урока:

Образовательная (учебная).

Сформировать умения и навыки метода устного решения квадратных уравнений.

Воспитательные.

Показать учащимся, что математические понятия не изолированы друг от друга, а представляют определенную систему знаний, все звенья которой находятся во взаимной связи.

— Формирование общественных навыков:

1. Вычислительных;
2. Эстетических навыков при оформлении записей;
3. Приобретение навыков исследовательской работы.

— Формирование качеств личности.

1. Трудолюбия;
2. Самостоятельности;
3. Ответственности за принятое решение.

Развивающие задачи:

1. Развитие мыслительной деятельности: умения анализировать, обобщать, классифицировать;
2. Развитие творческой деятельности: интуиции, смекалки.

Актуализация знаний.

На доске записано: ах 2 + bх + с, где а 0

— Что написано на доске? (Квадратный трехчлен)
— А теперь что написано на доске? ах 2 + bх + с = 0, где а 0 (Квадратное уравнение)
— Всегда ли имеют ли корни квадратный трехчлен и квадратное уравнение? (Нет, не всегда)
— От чего зависит количество корней? (От дискриминанта)
— Как найти дискриминант квадратного трехчлена или квадратного уравнения? (Д = в 2 – 4ас)
— Сколько корней в зависимости от дискриминанта может иметь квадратный трехчлен или квадратное уравнение? (Два различных корня, два одинаковых корня или нет корней).
— Как найти корни квадратного трехчлена или квадратного уравнения? (х_1,2 = )
— По какой формуле можно квадратный трехчлен разложить на линейные множители? (ах 2 + bх + с =а(х – х₁)(х – х₂))

1. Найдите корни квадратного трехчлена: 5х 2 + 8х + 3;
(Ответ: )

2. Решите квадратное уравнение: х 2 + 6х + 8 = 0;
(Ответ: -4 и -2)

3. Разложите на линейные множители квадратный трехчлен: 3х 2 – 10х + 8;
(Ответ: 3(х — 2)(х — ))

Введение знаний.

— Решая математические задачи, часто приходится встречаться с квадратными уравнениями. Поэтому помимо основных формул для вычисления корней таких уравнений полезно знать методы устного решения. Это помогает не только экономить время, но и развивать внимание. Конечно, не каждое квадратное уравнение можно решить с помощью свойства его коэффициентов, но в школьных учебниках многие уравнения решаются таким способом.

Свойства коэффициентов квадратного уравнения.

Пусть ах 2 + bх + с = 0, где а 0

1. Если а + b + с = 0, то х₁ = 1, х₂ = ;
2. Если а + с = b, то х₁ = -1, х₂ = —.

Пример 1. Решить уравнение: 341х 2 + 290х – 51 = 0

Решение. Имеем: а = 341, b = 290, с = -51.

341 + (-51) = 290, т.е. а + с = b. Следовательно, х₁ = -1, х₂ = .

Пример 2. Решить уравнение: 67х 2 – 75х + 8 = 0.

Решение. Замечаем, что 67 + 8 = 75, следовательно, х₁ = = 1, х₂ = .

Пример 3. Решить уравнение: 19х 2 + 15х – 34 = 0.

Решение. Так как 19 + 15 – 34 = 0, то искомые числители дробей равны 19 и -34, тогда, х₁ = = 1, х₂ = —.

Задания для закрепления.

1. 3х 2 – 5х + 2 = 0;
2. 2х 2 + 3х + 1 = 0;
3. 5х 2 + 9х –14 = 0;
4. 5х 2 + х – 6 = 0;
5. 5х 2 + 4х — 9 = 0;
6. х 2 + 29х – 30 = 0;
7. х 2 — 2000х – 2001 = 0;
8. 72х 2 + 69х – 3 = 0;
9. 83х 2 – 97х + 14 = 0.

Квадратное уравнение с коэффициентом 1 при х 2 ( т.е.а = 1) называют приведенным квадратным уравнением.

— Посмотрите на таблицу. Все ли уравнения , записанные в ней, являются приведенными квадратными уравнениями?

(Далее решаем уравнения из таблицы и все последовательно заполняем)

Сообщаю, что домашнее задание – закончить заполнение таблицы.

Подведение итогов обучения.

Видео:СВОЙСТВО КОЭФФИЦИЕНТОВ КВАДРАТНОГО УРАВНЕНИЯСкачать

Свойства коэффициентов в квадратном уравнении

Этот способ решения помогает не только сэкономить время, но и развить внимание.

Дано квадратное уравнение ax 2 + bx + c = 0 . Если a + b + c = 0 (сумма коэффициентов), то

Дано квадратное уравнение ax 2 + bx + c = 0 . Если a — b + c = 0 (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то

341x 2 + 290x — 51 = 0

Здесь, a = 341, b = 290, c = -51.

Проверим удовлетворяют ли коэффициенты условию

341 — 51 = 290. Получим а + с = b. Следовательно, мы

можем воспользоваться свойством 2.

Если в квадратном уравнении ax 2 + bx + c = 0 . Коэффициент b представлен в виде 2k, т.е. является четным числом, то формулу корней уравнения можно переписать в более простом виде

🎬 Видео

СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

СВОЙСТВО КОЭФФИЦИЕНТОВ КВАДРАТНОГО УРАВНЕНИЯСкачать

СВОЙСТВО КОЭФФИЦИЕНТОВ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратные уравнения #shorts Как решать квадратные уравненияСкачать

Квадратные уравнения: Свойства коэффициентовСкачать

коэффициенты в квадратном уравненииСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Теорема Виета. 8 класс.Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

ЕГЭ-2018. Задание В-5. Решение квадратного уравнения по сумме коэффициентов.Скачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение квадратных уравнений. Свойства коэффициентовСкачать

Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Как быстро решить квадратное уравнение. Замечательные свойства коэффициентов.Скачать

Как решать квадратные уравнения? ЧАСТЬ 7 - СВОЙСТВА КОЭФФИЦИЕНТОВ | Подготовка к ОГЭ и ЕГЭСкачать
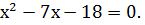