Свойства коэффициентов квадратного уравнения с доказательством

Видео:Свойства коэффициентов квадратного уравненияСкачать

этап. Свойства коэффициентов для быстрого нахождения корней квадратного уравнения.

Свойство 1. Если в уравнении ах 2 + bх +с = 0, а + b + с = 0, то один из его корней равен 1, а другой, в соответствии с теоремой Виета, равен с/а.

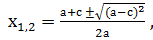
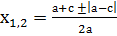
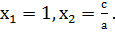
Доказательство: Имеем а+b+с=0, тогда b= — (а+с). Найдем дискриминант D=b 2 -4ас= а 2 +2ас+с 2 — 4ас = а 2 — 2ас+с 2 =(а — с) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

Пример 1: х 2 + х – 2 = 0; а = 1, в = 1, с = -2. Так как 1+1–2 =0, то х₁ =1, х₂ = -2.

Свойство 2. Если в уравнении ах 2 + bх + с = 0, а – b + с = 0 или b=a+c, то один из его корней равен –1, а другой –с/а .

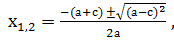
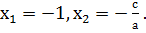
Доказательство: Имеем а — b+с=0, тогда b= а+с. Найдем дискриминант D=b 2 -4ас= а 2 +2ас+с 2 — 4ас = а 2 — 2ас+с 2 =(а — с) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

Пример 2 : х 2 – х – 2 = 0. Так как 1 – (- 1 ) + ( -2 ) = 0, то х₁ = -1, х₂ = 2.

Свойство 3. Если a = c, b = a 2 + 1, то x₁ = — a, x₂ = -1/a.

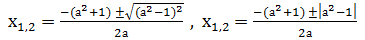
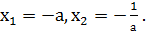
Доказательство: Имеем a = c, b = a 2 + 1. Найдем дискриминант D=b 2 -4ас= а 4 +2а 2 +1 — 4а 2 = а 4 — 2а 2 +1=(а 2 — 1) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

Пример 3. 3х 2 +10х+3=0, а=3, b=10, с=3. Так как а=с=3, b=3 2 +1=10, то х₁= -3, х₂=-1/3.

Свойство 4. Если a = c, b = -(a 2 + 1), то x₁ = a, x₂ = 1/a.

Доказательство: Имеем a = c, b = -(a 2 + 1). Найдем дискриминант D=b 2 -4ас= а 4 +2а 2 +1 — 4а 2 = а 4 — 2а 2 +1=(а 2 — 1) 2 . Формула корней этого квадратного уравнения имеет вид: . Отсюда имеем Что и требовалось доказать.

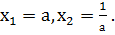
Пример 4. 3х 2 — 10х+3=0, а=3,b=-10,с=3. Так как а=с=3, b=-(3 2 +1)=-10, то х₁=3, х₂=1/3.

Приём переброски.

, первый коэффициент в качестве множителя «перебрасываем к -3», получим уравнение

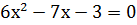
Корни 9 и -2 . Делим числа 9 и ( -2) на 6:

Ответ:

6 этап. Практическая направленность.

Задания, при решении которых необходимо умение решать квадратные уравнения.

Уровень А. 1. Найдите сумму и произведение корней уравнения: 2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны 2 и 5.

Уровень В. 2. Найдите сумму и произведение корней уравнения: 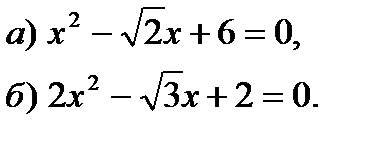2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны и .

Уровень С. Решите уравнение и выполните проверку по теореме, обратной теореме Виета: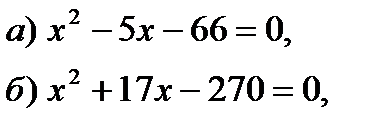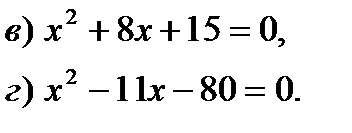

С помощью квадратных уравнений можно решать многие текстовые задачи. Вот одна из задач знаменитого индийского математика XII в. Бхаскары, решить ее можно с помощью квадратного уравнения.

На две партии разбившись, забавлялись обезьяны.

Часть восьмая их в квадрате в роще весело резвилась;

Криком радостным двенадцать воздух свежий оглашали…

Вместе сколько, ты мне скажешь, обезьян там было в роще?

1. Проводя исследование, выяснили, что кроме традиционных методов решения квадратного уравнения , которые мы узнали на уроках математики, существуют еще не менее интересные, а главные полезные свойства, практически устного решения квадратного уравнения.

2. Исследовательскую работу по математике планируем продолжать и далее.

3. Результаты своего исследования я представила в виде карточки-памятки( приложение 1) по решению квадратного уравнения.

· А.П.Ершова, В.В.Голобородько, А.С.Ершова «Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса», «ИЛЕКСА»,Москва,2003 .

· М.Б.Миндюк, Н.Г.Миндюк «Разноуровневые дидактические материалы по алгебре, 8 класс», «ГЕНЖЕР»,Москва,2002.

· «Алгебра 7-9 .Тематические зачеты»

· Г.И.Ковалева «Уроки математики в 8 классе»,издательство «БРАТЬЯ ГРИНИНЫ»,Волгоград, 2001.

Видео:СВОЙСТВО КОЭФФИЦИЕНТОВ КВАДРАТНОГО УРАВНЕНИЯСкачать

Теорема Виета и её применение

Разделы: Математика

Цель:

• Обобщить и закрепить навыки решения квадратных уравнений ах 2 + вх + с = 0, в которых а + в + с = 0; продолжить развивать навыки устного решения таких уравнений.
• Способствовать выработке у школьников желания и потребности обощения изучаемых фактов: развивать самостоятельность и творчество.
• Обеспечить закрепление теоремы на интересных примерах.

Оборудование:

• Кодоскоп
• Карточки тесты
• Карточки с индивидуальными заданиями для учащихся
• Сигнальные карточки.

Ход урока

I Повторение пройденного материала

1) Устная работа через кодоскоп с применением сигнальных карточек. Если ученик готов отвечать, то зеленая, нет – красная. Согласен с ответом – зеленая, не согласен – красная.

А) 5х 2 – 7х + 2 = 0	[т.к. а + в + с = 0, то х1 = 1, х2 = ]
Б) х 2 – 12х + 35 = 0	[по обратной теореме Виета х1 = 7, х2 = 5]
В) 313х 2 + 326х + 13 = 0	[а – в + с = 0, то х1 = –1, х2 = –]
Г) 4х 2 + 12х + 5 = 0	[метод переброски х1 = –, х2 = –]
Д) Составьте квадратное уравнение, если известны его корни:
х1 = 5, х2 = –6	[ х 2 + х –30 = 0]
х1 = 2, х2 =	[ х 2 – (2 – ) х + 2 = 0]

Доказательство теоремы Виета и свойств числовых коэффициентов уравнения.

Теорема Виета.

Сумма корней квадратного уравнения равна коэффициенту при х, взятому с противоположным знаком и деленному на коэффициент при х 2 ; произведение корней этого уравнения равно свободному члену деленному на коэффициент при х 2 .

х₁ + х₂ = –

х₁х₂ = .

Т.к. квадратное уравнение ах 2 + вх + с = 0 имеет корни х₁ и х₂, то справедливо тождество ах 2 + вх + с = а(х – х₁)(х – х₂).

Раскроем скобки в правой части этого тождества:

х 2 + х – х₂х + х₁х₂,

отсюда следует, что х₁ + х₂ = – и х₁* х₂ = . Что и требовалось доказать.

Обратная теорема Виета.

Если выполняются равенства х₁ + х₂ = – и х₁х₂ = , то числа х₁ и х₂ являются корнями уравнения ах 2 + вх + с = 0.

Свойства коэффициентов 1.

Пусть дано квадратное уравнение ах 2 + вх + с = 0, где а0. Если а + в + с = 0, то х₁ = 1, х₂ = .

ах 2 + вх + с = 0, а0

Разделим обе части уравнения на а0, получим приведенное квадратное уравнение х 2 + .

Согласно теореме Виета		х1 + х2 = –
		х1

По условию а + в + с = 0, откуда в = – а – с. Значит		х1 + х2 = – = 1 +
		х1* х2 = 1 *

Получим х₁ = 1, х₂ = .

Свойство коэффициентов 2.

Если в квадратном уравнении ах 2 + вх + с = 0 а – в + с = 0, то х₁ = – 1, х₂ = – .

В итоге на доске открывается таблица:

Связь между корнями и коэффициентами квадратного уравнения.

Уравнение	Условие	Заключение	Пример
ах 2 + вх + с = 0	х1 и х2	х1 + х2 = – , х1 * х2 =	х1 = 7 + ; х2 = 2 –

х₁ + х₂ = 9; х₁х₂ = 11 – 5ах 2 + вх + с = 0х₁ + х₂ = – , х₁ * х₂ = х₁ и х₂ корних 2 + 5х + 6 = 0

х₁ = – 2, х₂ = – 3ах 2 + вх + с = 0а + в + с = 0х₁ = 1, х₁ = 1998х 2 – 907х – 1091 = 0

х₁ = 1, х₂ = ах 2 + вх + с = 0а – в + с = 0х₁ = – 1, х₁ = – 127х 2 + 250х + 123 = 0

х₁ = – 1, х₁ = – ах 2 + вх + с = 0а 2 х 2 + авх + ас = 0

у₁, у₂х₁ =

х₂ = 4х 2 + 12х + 5 = 0

у 2 + 12у + 20 = 0

х₁ = – , х₂ = – ;

у₁ = – 2, у₂ = – 10.

По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше скажи постоянства такого:
Умножишь ты корни – и дробь уж готова?!
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в, в знаменателе а.

II. Решение интересных заданий с применением теоремы Виета. Классу задается на дом подобрать по три интересных задания. Самые интересные решаются на уроке. №1 и №2 решаются на доске одновременно. №1 решается с полным комментированием, класс работает с учеником, который решает №1. №2 ученик рассказывает основные моменты.

1. Найдите сумму квадратов всех корней уравнения х 2 – 3e х? + 1 = 0.

	х 2 + 3х + 1 = 0;	х1 + х2 = – 3;	х1 * х2 = 1;
	х 2 – 3х + 1 = 0;	х3 + х4 = 3;	х1 * х2 = 1;

х + х + х + х = (х₁ + х₂) 2 – 2х₁х₂ + (х₃х₄) 2 – 2х₃х₄ = 9 – 2 + 9 – 2 = 14.

2. Пусть х₁ и х₂ – корни уравнения 2х 2 – 7х + 1 = 0. Составьте квадратное уравнение, корнями которого являются числа и .

Для составления квадратного уравнения с заданными корнями и воспользуемся теоремой, обратной теореме Виета, для этого необходимо найти их сумму и произведение:

+ = = = = 150,5

– = = = 2.

Искомое уравнение имеет вид

х 2 + 150,5 + 2 = 0 или 2х 2 – 301х + 4 = 0.

3. Корни уравнения х 2 – вх – в = 0 таковы, что х + х + хх = 7,5.

х + х = (х)(( х) – 3х) + х = b(b + 3b) – b 3 = b 3 + 3b 2 – b 3 = 3b 2 = 75.

4. Пусть х₁и х₂ корни уравнения 3х 2 + 14х – 4 = 0.

Установите, больше или меньше единицы значение дроби

.

х₁ + х₂ = – ;

х₁ * х₂ = – ;

5. Для каких значений а разность корней уравнения 2х 2 – (а + 1)х + а + 3 = 0 равна единице?

х₁ + х₂ = = > 1 + х₁ + х₂ =

х₁ * х₂ = = > 2х₂ + 1 = = > х₂ = .

х₁ = 1 +

х₁ =

= ;

(а + 3)(а – 1) = 8а + 24

а 2 + 3а – а – 3 – 8а – 24 = 0

III. Тест – самостоятельная по карточкам.

Установите верный ответ из числа предложенных А), Б), В), Г).

х 2 + (

А) 2; ;

Б) ——;

В); ;

Г) нет правильных ответов.

Не решая квадратного уравнения 3х 2 -х-11 = 0, составьте квадратное уравнение, корнями которого являются числа и .

А) х 2 —

Б) х 2 —

В) х 2 +

Г) х 2 +

Установите верный ответ из числа предложенных А), Б), В), Г).

1) Решите уравнение:

х 2 -(

А) 5; ;

Б) ——;

В) —; ;

Г) ; .

Не решая квадратного уравнения 2х 2 -5х-4 = 0, составьте квадратное уравнение, корнями которого являются числа и .

А) х 2 —

Б) х 2 —

В) х 2 +

Г) х 2 +

Проверка ответов через кодоскоп. Учащиеся меняются листочками с ответами, проверяют решение соседа и ставят оценку.

IV. Домашнее задание

Поменяться карточками с творческими заданиями.

Видео:СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

Свойства коэффициентов квадратного уравнения с доказательством

Этот способ решения помогает не только сэкономить время, но и развить внимание.

Дано квадратное уравнение ax 2 + bx + c = 0 . Если a + b + c = 0 (сумма коэффициентов), то

Дано квадратное уравнение ax 2 + bx + c = 0 . Если a — b + c = 0 (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то

341x 2 + 290x — 51 = 0

Здесь, a = 341, b = 290, c = -51.

Проверим удовлетворяют ли коэффициенты условию

341 — 51 = 290. Получим а + с = b. Следовательно, мы

можем воспользоваться свойством 2.

Если в квадратном уравнении ax 2 + bx + c = 0 . Коэффициент b представлен в виде 2k, т.е. является четным числом, то формулу корней уравнения можно переписать в более простом виде

🎦 Видео

Теорема Виета. 8 класс.Скачать

Квадратные уравнения: Свойства коэффициентовСкачать

СВОЙСТВО КОЭФФИЦИЕНТОВ КВАДРАТНОГО УРАВНЕНИЯСкачать

Метод переброски в квадратных уравнениях. ЕГЭ и ОГЭ 2022 по математикеСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

коэффициенты в квадратном уравненииСкачать

Квадратные уравнения #shorts Как решать квадратные уравненияСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Частные случаи решения квадратных уравнений Решение уравнений с использованием свойств коэффициентовСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

ЕГЭ-2018. Задание В-5. Решение квадратного уравнения по сумме коэффициентов.Скачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Квадратные уравнения | Формулы для коэффициентов | АлгебраСкачать

Квадратные уравнения.Скачать

Доказательство формулы корней квадратного уравненияСкачать