Алгебра и теория чисел
Лекция 3
Системы линейных уравнений
План
1. Основные понятия и обозначения.
2. Элементарные преобразования системы линейных уравнений.
3. Ступенчатая матрица. Приведение матрицы к ступенчатому виду.
Литература
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 25-48.
2. Ермаков В.И. Общий курс высшей математики. М.: Инфра — М, 2000. с. 5-22
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 38-56.
1. Основные понятия и обозначения. Простейшие системы двух линейных уравнений с двумя неизвестными изучаются в средней школе:

Известно, что справедлив один из следующих трех случаев: либо система имет одно решение, либо имеет бесконечно много решений, либо не имеет решений. В этом параграфе мы будем рассматривать общие системы линейных уравнений и установим это утверждение в общем случае кроме того изложим один из наиболее удобных методов решения систем линейных уравнений — метод последовательного исключения неизвестных или метод Гаусса по имени выдающегося немецкого математика К. Ф. Гаусса (1777-1855).
Определение 1.Системой m линейных уравнений с n неизвестными

где a11 ,a12 . amn — фиксированные числа (действительные, комплексные или принадлежащие некоторому полю) , называемые коэффициентами при неизвестных, b1 ,b2 . bm — фиксированные числа, называемые свободными членами.
Если все свободные члены в системе линейных уравнений равны нулю, то система линейных уравнений называется однородной.
Определение 2.Решением системы линейных уравнений (1) называется такой упорядоченный набор n чисел 
Система называется совместной, если она имеет хотя бы одно решение, и называется несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет одно решение, и называется неопределенной, если она не имеет решений.
Пусть S1 , S2 системы линейных уравнений с одним и тем же числом неизвестных, X1 , X2 — множества их решений соответственно.
Определение 3.Говорят, что система линейных уравнений S2 следствие системы S1 и S2 , если каждое решение системы S1 является решением системы S2 ,т.е. 

Определение 4. Говорят, что системы S1 и S2 равносильны, если каждое решение системы S1 является решением системы S2 и каждое решение системы S2 является решением системы S1 , т.е. 

Отношение следования и равносильности обладают следующими свойствами.
1. Если 


Действительно, если 

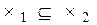



2. 
3. Если 

4. Если 
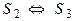
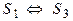
Свойства 2, 3, 4 доказываются аналогично.
Элементарные преобразования системы линейных уравнений.
Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:
1) перестановка любых двух уравнений местами;
2) умножение обеих частей одного уравнения на любое число 
3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;
(при этом все остальные уравнения остаются неизменными).
Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.
Доказательство.В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.
1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной .
2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число 

Пусть 






Умножая его на число k,получим верное числовое равенство:

т.о. устанавливаем, что 
Обратно, если 





Отсюда по определению 4 система (1) равносильна системе (2).
3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы . Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число k , получим систему

Пусть 




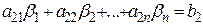
Прибавляя почленно к первому равенству второе, умноженное на число k получим верное числовое равенство:

Обратно, если 



Отсюда по определению 4 система (1) равносильна системе (5).
4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.
Ступенчатая матрица.
Определение 6.Матрицей размерности 
содержащая mn чисел, расположенных в m строк и n столбцов, числа 

Определение 7. Матрицей ступенчатого вида называется такая матрица, которая обладает свойствами:
1) в каждой строке матрицы имеется неравный нулю элемент;
2) в каждой строке матрицы, начиная со второй, первый слева неравный нулю элемент расположен правее первого слева неравного нулю элемента предыдущей строки матрицы.
Матрицу ступенчатого вида называют также трапециидальной матрицей, а квадратную матрицу ступенчатого вида называют треугольной матрицей. Ниже показаны две не ступенчатые матрицы и три ступенчатые матрицы (последняя матрица треугольная).







Определение 8. Элементарными преобразованиями строк матрицы называются следующие ее преобразования:
1) перестановка любых двух строк матрицы местами;
2) умножение одной строки матрицы на любое число 
3) прибавление к одной строке матрицы другой ее строки умноженной на любое число k ;
(при этом все остальные строки матрицы остаются неизменными).
Аналогично можно рассматривать элементарные преобразования столбцов матрицы.
Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований вычеркивания нулевой строки можно привести к матрице ступенчатого вида.
Доказательство.Доказательство проводим методом математической индукции по числу m строк матрицы. Для m=1 утверждение теоремы справедливо, так как ненулевая однострочная матрица по определению имеет ступенчатый вид.
Предположим, что утверждение теоремы доказано для матриц, имеющих m-1 строку и докажем его для матриц, в которых содержится m строк. Пусть первый слева отличный от нуля столбец данной матрицы имеет номер k , так как матрица ненулевая, то такой столбец найдется, и матрица имеет вид:
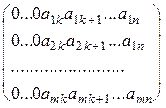
Можем считать, что элемент 




Рассмотрим матрицу, состоящую из последних m-1 строк матрицы (9):

Если матрица (10) нулевая, то все строки в матрице (9) кроме первой нулевые. Вычеркивая их, приходим к матрице ступенчатого вида. Если матрица (10) ненулевая, то по индуктивному предположению конечным число элементарных преобразований и преобразований вычеркивания нулевой строки может быть приведена к матрице ступенчатого вида: 
где элементы 



элементы 


4. Метод Гаусса. Системе линейных уравнений (1) соответствуют три матриц



Первая матрица называется матрицей системы, вторая — расширенной или присойдиненной матрицей системы, третья — столбцом свободных членов.
Система линейных уравнений называется системой ступенчатого вида, если расширенная матрица системы есть матрица ступенчатого вида. Неизвестные с коэффициентами неравными нулю, которые стоят первыми в уравнениях системы ступенчатого вида называются главными неизвестными, а остальные неизвестные называются свободными.
Линейное уравнение, в котором все коэффициенты равны нулю, а свободный член не равен нулю, т.е. уравнение вида:

не имеет решений. Действительно, если 

Пусть не все уравнения системы (1) нулевые. Тогда и расширенная матрица системы (1) ненулевая. По теореме 2 ее можно конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида. Полученной матрице соответствует система линейных уравнений ступенчатого вида. Этим преобразованиям расширенной матрицы системы (1) соответствуют такие же преобразования системы линейных уравнений (1). По теореме 1 они переводят систему (1) в равносильную систему линейных уравнений, которая будет являются системой ступенчатого вида.
Таким образом мы доказали первую часть следующей теоремы.
Теорема 3.Любую систему линейных уравнений , содержащую ненулевое уравнение конечным числом элементарных преобразований и преобразований вычеркивания нулевого уравнения можно привести к равносильной ей системе ступенчатого вида. При этом возможны следующие три случая.
1. Если в полученной системе линейных уравнений ступенчатого вида есть противоречивое уравнение, то данная система не имеет решений.
2. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе равно числу неизвестных, то данная система имеет единственное решение.
3. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе меньше числа неизвестных, то данная система имеет бесконечно много решение.
Доказательство.Пусть дана система (1), содержащая ненулевое уравнение. По выше доказанному, она конечным числом элементарных преобразований она может быть преобразована к равносильной ей системе уравнений ступенчатого вида. Возможны случаи.
В полученной системе ступенчатого вида есть противоречивое уравнение. Тогда ни один набор чисел 
В полученной системе ступенчатого вида нет противоречивого уравнения. Тогда в каждом из уравнений системы ступенчатого вида содержится главное неизвестное. Отсюда получаем, что число главных неизвестных, а тем более число всех неизвестных, не менее числа уравнений в системе ступенчатого вида. Тогда возможны под случаи:
В системе ступенчатого вида число уравнений равно числу неизвестных, т. е. система имеет вид:

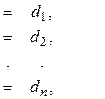
где 


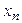




В системе ступенчатого вида число уравнений меньше числа неизвестных. В этом случае матрица полученной системы имеет вид (11), а
систему можно записать в виде:




где 




Следствие.Если в системе однородных уравнений число неизвестных больше числа уравнений, то система имеет бесконечно много решений.
Действительно, система однородных уравнений всегда имеет нулевое решение 
Метод исследования и решения систем линейных уравнений, изложенный в доказательстве теорем 3 называется методом Гаусса.
Пример 1.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Составим по полученной матрице ступенчатого вида систему линейных уравнений ступенчатого вида:
В полученной системе число уравнений равно числу неизвестных и полученная система имеет единственное решение, которое двигаясь вверх последовательно находим:
Решение системы 
Пример 2.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Видео:Решение системы уравнений методом ГауссаСкачать

02. Элементарные преобразования системы линейных уравнений
Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:
1) перестановка любых двух уравнений местами;
2) умножение обеих частей одного уравнения на любое число 
3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;
(при этом все остальные уравнения остаются неизменными).
Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.
Доказательство. В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.
1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной.
2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число 

Пусть 






Умножая его на число K, получим верное числовое равенство:

Т. о. устанавливаем, что 
Обратно, если 





Отсюда по определению 4 система (1) равносильна системе (2).
3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы. Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число K , получим систему

Пусть 





Прибавляя почленно к первому равенству второе, умноженное на число K получим верное числовое равенство:

Обратно, если 



Отсюда по определению 4 система (1) равносильна системе (5).
4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Системы линейных уравнений
Глава 5. Системы линейных уравнений
Определение. Матрицей называется прямоугольная таблица, составленная из чисел.
Числа, записанные в матрице, называются её элементами. При этом они могут быть как действительными, так и комплексными. Пример:
A =
Наша матрица A состоит из 3 строк и 4 столбцов. Будем записывать это так, что (3, 4) − размер матрицы A (иногда пишут 3×4, но × легко перепутать с x, особливо в рукописном тексте). Вообще, если в матрице s строк и n столбцов, то её размером считается запись (s, n). Матрицу обрамляют круглыми скобками: (). В литературе вы можете встретить другие обозначения: || || или []. Если s = n, то матрица называется квадратною. Матрицу размера (n, n) называют также квадратною матрицею n—го порядка.
Если надобно записать матрицу в общем (буквенном) виде, то пишут так:
A =
Это матрица размера (s, n), каждый её элемент обозначен одной и той же буквою − обыкновенно (хотя и не обязательно) это та же буква, которая обозначает самоё матрицу, но строчная. Эта буква снабжена двойными индексами: a11 − это не ‘a одиннадцать’, а ‘a один-один’. Первый индекс означает номер строки, в которой стоит данный элемент, второй − номер столбца. Разделителей между индексами обыкновенно не пишут, доколе это не может привести к неопределённости; к примеру, запись a211 непонятна: не то это a2,11, не то a21,1. В этом случае разделитель обязателен (здесь это запятая).
Среди всех матриц выделим матрицы, состоящие из одного столбца, т. е. размера (s, 1):

Такую матрицу назовём матрицей—столбцом, или вектор—столбцом. Аналогично матрицу вида
размера (1, n) назовём матрицей—строкой, или вектор—строкой.
5.1.2. Ступенчатая матрица
Определение 1. Строка матрицы называется нулевой строкой, если она состоит из одних нулей.
Определение 2. Главным элементом какой-либо ненулевой строки данной матрицы называется первый ненулевой элемент этой строки, считая слева направо.
Нулевая строка не имеет главного элемента, все остальные строки имеют однозначно определённый главный элемент. В любой матрице число главных элементов равно числу ненулевых строк.
Определение 3. Матрица называется ступенчатой, если для любых двух её последовательных строк выполняется одно из двух условий:
1) вторая строка состоит из одних нулей (нулевая строка);
2) обе строки ненулевые, и при этом главный элемент первой строки расположен строго левее главного элемента второй строки.
Из этого определения легко понять, что нулевые строки концентрируются в конце (внизу) матрицы, составляя нулевой блок (блок нулевых строк). В самом деле, если какая-либо строка нулевая, то в силу первой части определения все последующие строки также нулевые. Впрочем, нулевых строк может и вовсе не быть.
Определение 4. Матрица называется главной ступенчатой, если она является ступенчатой и сверх того
3) все главные элементы равны единице;
4) выше главных единиц (в тех же столбцах) стоят одни нули.
Из определения ясно, что каждый главный столбец главной ступенчатой матрицы устроен так, что в одной позиции стоит 1, а в остальных позициях − нули. (Ниже 1 стоят нули из-за того, что матрица является ступенчатой.) При этом номер позиции (строки), в которой стоит 1, равен номеру этого столбца в череде главных столбцов.
5.1.3. Элементарные преобразования
Определение 1. Элементарным преобразованием первого типа над строками какой-либо матрицы называется перестановка местами двух произвольных строк этой матрицы.
Определение 2. Элементарным преобразованием второго типа называется умножение произвольной строки данной матрицы на какое-либо число, не равное 0.
Определение 3. Элементарным преобразованием третьего типа называется прибавление к какой-либо строке данной матрицы другой строки, умноженной предварительно на любое число[1].
5.1.4. Теорема C. F. Gauss’а[2]
Теорема (C. F. Gauss’а). Любую матрицу с помощью нескольких элементарных преобразований над строками можно привести к главному ступенчатому виду.
Доказательство. Будем рассматривать матрицы размера (s, n). Обозначим через N сумму числа строк и столбцов: N = s + n. Доказательство поведём индукцией по этому параметру N. Наименьшее возможное значение N равно 2 (для матриц размера (1, 1)).
Основание (база) индукции. Пусть наша матрица A имеет размер (1, 1). Тогда A = = (a11). Если a11 = 0, то матрица уже главная ступенчатая. Если же нет, то разделим (единственную) строку матрицы A на a11, получим матрицу (1), которая уже является главной ступенчатой.
Индуктивный переход. Пусть теорема C. F. Gauss’а справедлива для любой матрицы, у которой s + n 1 вычтем из i-й строки матрицы D её первую строку, предварительно умножив её на число di1. После этой серии элементарных преобразований в новой матрице E все элементы первого столбца, кроме первого, станут равными нулю. Обозначим через F матрицу, получающуюся из E вычёркиванием первой строки и первого столбца. Её размеры меньше размеров матрицы A, и поэтому её можно привести к главному ступенчатому виду G с помощью серии элементарных преобразований над её строками, что равносильно совершению таких же элементарных преобразований над матрицей E. Пусть матрица E привелась таким образом к матрице H. Матрица H уже ступенчатая, но не обязательно главная ступенчатая. Возьмём какой-нибудь главный столбец матрицы G. Пусть главная единица нашего столбца стоит в k-й строке и l-м столбце матрицы H.
Вычтем из первой строки матрицы H её k-ю строку, умноженную предварительно на число h1l, и первый элемент нашего столбца обнулится. Важно, что при этом никак не затрагивается первый столбец, − он остаётся неизменным. Произведём указанную операцию с каждым главным столбцом матрицы G. Ясно, что новая матрица уже будет главной ступенчатой. Теорема доказана.
5.1.5. Обратимость элементарных преобразований
Предложение. Если над матрицей A совершено элементарное преобразование какого-либо типа, приводящее её к матрице B, то существует элементарное преобразование того же типа, приводящее матрицу B снова к матрице A.
Доказательство. Это очевидно для преобразований первого и второго типов. В самом деле, если мы совершили перестановку строк, то вторичная перестановка тех же строк вернёт нас к исходной матрице. Если мы умножили некоторую строку на ненулевое число, то умножение той же строки на обратное число вернёт нас к исходной матрице. Допустим теперь, что в данной матрице A мы прибавили к i-й строке j-ю строку (i ≠ j), предварительно умноженную на число α, и таким образом пришли к матрице B. Утверждаю, что можно вернуться к матрице A, если прибавить к i-й строке матрицы B её j-ю строку, предварительно умноженную на число −α. Так как при обоих преобразованиях все строки, кроме i-й, вообще не менялись, то достаточно посмотреть, что произойдёт с каким-нибудь элементом bik матрицы B. Вычисляем:
т. е. мы вернулись к матрице A, QED.
§ 5.2. Системы линейных уравнений
5.2.1. Основные определения
Определение 1. Система уравнений вида
называется системой линейных алгебраических уравнений с неизвестными x1, x2, …, xn.
Числа aij называются коэффициентами системы, bi − её свободными членами.
Определение 2. Решением системы (1) называется такой набор чисел 
Определение 3. Решить систему (1) − значит найти все её решения (множество всех решений).
Определение 4. Система (1) называется совместною, если она имеет хотя бы одно решение (множество всех решений непусто), и несовместною в противном случае, т. е. если она не имеет решений (множество всех решений пусто).
Определение 5. Система (1) называется определённою, если она имеет ровно одно решение, и неопределённою, если имеет более одного решения.
Мы очень скоро увидим, что неопределённая система имеет бесконечно много решений.
5.2.2. Элементарные преобразования над системами уравнений
Определение 1. Элементарным преобразованием первого типа над системой уравнений называется перестановка местами двух произвольных уравнений системы.
Определение 2. Элементарным преобразованием второго типа называется умножение любого уравнения системы на какое-либо число, не равное 0.
Определение 3. Элементарным преобразованием третьего типа называется прибавление к какому-либо уравнению другого уравнения, умноженного предварительно на любое число[3].
Каждой системе уравнений вида (1) можно поставить в соответствие две матрицы: матрицу системы и расширенную матрицу системы.
Определение 4. Матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы:

Определение 5. Расширенной матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы и свободных членов:

Иногда в расширенной матрице отделяют столбец свободных членов вертикальной чертой (сплошной или прерывистой), но это не обязательно. Ясно, что матрица системы не даёт полной информации о системе в отличие от расширенной матрицы, по которой можно однозначно восстановить систему уравнений, если только мы знаем список неизвестных (буквы, которыми были обозначены неизвестные). Впрочем, последнее не так существенно, потому что ведь мы в первую очередь интересуемся решениями, а каждое решение представляет собою просто набор чисел без обозначений неизвестных.
Определение 6. Пусть даны две системы уравнений относительно одного и того же набора неизвестных x1, x2, …, xn. Говорят, что система (2) является следствием системы (1), если каждое решение системы (1) является решением системы (2).
Другими словами, множество всех решений системы (1) есть подмножество (часть) множества всех решений системы (2).
Определение 7. Две системы уравнений относительно одного и того же набора неизвестных x1, x2, …, xn называются эквивалентными, или равносильными, если множества их решений совпадают, или, что то же, каждая из них является следствием другой.
Иными словами, две системы эквивалентны тогда и только тогда, когда каждое решение первой системы является решением второй и, наоборот, каждое решение второй системы является решением первой.
Предложение. При совершении одного элементарного преобразования система уравнений переходит в эквивалентную систему.
Доказательство. Достаточно доказать, что вторая система является следствием первой. Действительно, предположив, что это уже доказано, совершим обратное элементарное преобразование, которое вернёт нас к исходной системе (см. п. 5.1.5). По доказанному первая система тогда будет следствием второй, и всё доказано.
Докажем, что вторая система является следствием первой. Для преобразований первых двух типов это совершенно очевидно. Совершим преобразование третьего типа, прибавив к i-й строке j-ю строку, умноженную предварительно на число α. При этом изменится только i-е уравнение, поэтому я здесь выпишу только его:
Пусть 
Если подставить наше решение в новую систему, то все равенства, кроме i-го, будут выглядеть точно так же и поэтому выполняются. i-е же равенство будет выглядеть так:
Чтобы убедиться, что оно тоже выполняется, достаточно взять i-е равенство системы (1*) верных числовых равенств и прибавить к нему j-е равенство той же системы, предварительно умножив его на α. Предложение доказано.
5.2.3. Теорема C. F. Gauss’а (о системах линейных уравнений)
Лемма. Если в системе линейных уравнений совершить одно элементарное преобразование, то расширенная матрица новой системы может быть получена из расширенной матрицы старой системы с помощью совершения аналогичного (точно такого же, я буду говорить одноимённого) преобразования.
Доказательство: это очевидно.
Следствие. Если в расширенной матрице A системы линейных уравнений (1) совершить одно элементарное преобразование над её строками и таким образом прийти к новой матрице B, а затем одноимённое преобразование совершить над системой уравнений (1), то расширенная матрица новой системы (2) совпадёт с матрицей B.
Доказательство. В силу леммы расширенная матрица системы (2) может быть получена из матрицы A, т. е. расширенной матрицы системы (1), с помощью совершения преобразования, одноимённого тому, которое было совершено нами над системой уравнений (1). С другой стороны, это последнее преобразование было одноимённо тому, которое мы совершили над матрицей A. Таким образом, расширенная матрица системы (2) может быть получена из A с помощью того же самого преобразования, которое мы в самом начале совершили над матрицей A. Значит, эта новая расширенная матрица совпадает с B, QED.
Теорема (C. F. Gauss’а, о системах линейных уравнений). Всякая система линейных уравнений с помощью конечного числа элементарных преобразований может быть приведена к такой системе уравнений, расширенная матрица которой является главной ступенчатой.
Доказательство. Приведём расширенную матрицу данной системы уравнений с помощью серии элементарных преобразований над её строками к главному ступенчатому виду. Теперь будем совершать над самой данной системой одноимённые преобразования. По следствию из леммы на каждом этапе очередная матрица будет расширенной матрицей соответствующей системы уравнений. Значит, и последняя, главная ступенчатая, матрица будет служить расширенной матрицей последней системы, QED.
Важно, что на каждом этапе в силу предложения из предыдущего пункта система уравнений переходит в эквивалентную. На этом основан метод C. F. Gauss’а решения систем, при котором система приводится с помощью серии элементарных преобразований к главному ступенчатому виду. Множество всех решений системы при этом не меняется, так что достаточно решить последнюю систему. А системы, имеющие главный ступенчатый вид, решаются очень легко, как будет видно из следующего пункта.
5.2.4. Решение ступенчатых систем уравнений
Рассмотрим систему линейных уравнений, расширенная матрица которой является главной ступенчатой. Допуская известную вольность речи, будем такие системы называть ступенчатыми.
Определение. В ступенчатой системе уравнений неизвестные, соответствующие главным столбцам, называются главными неизвестными, все остальные − свободными неизвестными.
Здесь надлежит различать три случая.
1°. Столбец свободных членов является главным. В этом случае система несовместна.
В самом деле, пусть главный элемент последнего столбца расширенной матрицы (т. е. столбца свободных членов) находится в i-й строке. Тогда i-е уравнение имеет следующий вид:
(Напомню, что все главные элементы главной ступенчатой матрицы равны 1, а левее любого главного элемента всегда стоят одни нули.) Ясно, что такое уравнение не имеет решений, тем более не может иметь решений вся наша система.
2°. Все столбцы, кроме последнего, главные. (Другими словами: нет свободных неизвестных, а столбец свободных членов не является главным, т. е. не содержит главных элементов.) В этом случае в i-м столбце на i-м месте стоит 1 (i ≤ n), на остальных местах − нули. После отбрасывания нулевых уравнений придём к эквивалентной системе, которая в нашем случае приобретает следующий вид:
Ясно, что такая система имеет решение, и притом единственное, а именно, 
3°. Есть свободные неизвестные, но столбец свободных членов не является главным. Покажем, что в этом случае система имеет бесконечно много решений (и, следовательно, является неопределённой). Отбросим в расширенной матрице нулевые строки (они сосредоточены внизу матрицы), что приведёт к эквивалентной системе. Можно считать, что исходная расширенная матрица не была нулевой (для нулевой матрицы доказываемое утверждение очевидно), так что хотя бы одна строка останется. Теперь число строк в матрице равно числу главных неизвестных. Для удобства переобозначим неизвестные: пусть y1, y2, …, yr − главные неизвестные, а z1, z2, …, zn−r − свободные. Разнесём теперь неизвестные в разные части: главные неизвестные оставим в левых частях уравнений, а свободные перенесём в правые части, естественно, с противоположным знаком (свободные члены также остаются в правых частях). Получится система, эквивалентная исходной, следующего вида:
Мы видим, что здесь все главные неизвестные явно выражены через свободные, причём эти выражения (правые части) представляют собою линейные функции, т. е. линейные комбинации свободных неизвестных плюс свободный член. Как же решить получившуюся систему? Придадим свободным неизвестным произвольные значения и вычислим по написанным формулам соответствующие значения главных неизвестных. Очевидно, что в совокупности мы получим решение нашей системы. Более того, каждое решение можно получить таким способом при подходящем выборе свободных неизвестных, так как все неизвестные всегда будут связаны соотношениями (3). В этом смысле формулы (3) описывают множество всех решений нашей системы, т. е задают, как говорят, её общее решение. И ясно, что решений будет бесконечно много, потому что хотя бы одно свободное неизвестное у нас есть, значит, придать определённые значения свободным неизвестным мы можем бесконечным числом различных способов, и получающиеся решения будут различны.
Попутно мы фактически доказали следующие два утверждения.
Теорема 1 (критерий совместности ступенчатой системы). Система уравнений, расширенная матрица которой имеет главный ступенчатый вид, совместна тогда и только тогда, когда столбец свободных членов не является главным.
Теорема 2. Если система линейных уравнений имеет более одного решения, то она имеет бесконечно много решений.
Таким образом, линейная система не может иметь, например, ровно семь решений.
5.2.5. Однородные системы уравнений
Так называются системы линейных уравнений, в которых все свободные члены равны нулю:
Такая система всегда совместна, т. к. она всегда имеет решение 
Теорема. Если в однородной системе линейных уравнений (4) число уравнений s строго меньше числа неизвестных n, то такая система имеет хотя бы одно нетривиальное решение.
Доказательство. Приведём нашу систему к главному ступенчатому виду. На всех этапах однородность, очевидно, сохраняется. После отбрасывания нулевых уравнений мы получим однородную систему уравнений, эквивалентную исходной. Число её уравнений строго меньше числа неизвестных, так как число неизвестных не изменилось, а число уравнений даже могло уменьшиться. Но число строк теперь равно числу главных элементов, а значит, числу главных столбцов и числу главных неизвестных. Таким образом, число главных неизвестных строго меньше общего числа неизвестных. Значит, есть свободные неизвестные, а тогда система неопределённая (нулевой столбец свободных членов не может быть главным) и имеет бесконечно много решений. Значит, есть и ненулевые решения, QED.
[1] При этом результат ставится в первую из этих двух строк, а вторая из них, равно как и все остальные строки матрицы, не меняется.
[2] ́дрих Га́усс (нем. Johann Carl Friedrich Gauß; 30 апреля 1777, Брауншвейг − 23 февраля 1855, Гёттинген) − великий немецкий математик, астроном и физик, считается одним из величайших математиков всех времён.
[3] При этом результат ставится на место первого из этих двух уравнений, а второе из них, равно как и все остальные, не меняется.
🔍 Видео
Математика без Ху!ни. Метод Гаусса.Скачать

Свойства определителя - bezbotvyСкачать

Элементарные преобразования матриц. Высшая математика.Скачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы уравнений методом Крамера.Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

11. Ранг матрицыСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Билет 2 (Элементарные преобразования, эквивалентность, метод Гаусса)Скачать

Матричный метод решения систем уравненийСкачать

Свойства систем линейных уравнений (01)Скачать

Линейная алгебра, 6 урок, Ранг матрицыСкачать


















