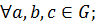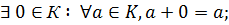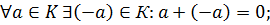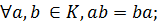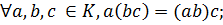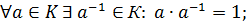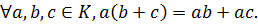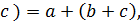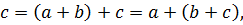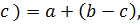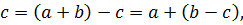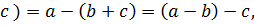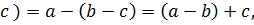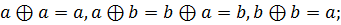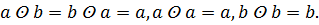Свойства бинарных операций разрешимость уравнений (5 видео)

Свойства бинарной алгебраической операции

АЛГЕБРА

(ЧАСТЬ 1)

Материалы для практических занятий

и самостоятельной работы

для студентов факультета МиИТ

Кафедра: «Алгебры, геометрии и методики преподавания

(направления 010100.62 «Математика»; 050100.62)

Составили: канд. физ.-мат. наук О.Н. Шатных.

Утверждены на заседании кафедры «19» ноября 2013 г.

Рекомендованы методическим советом университета

«23» декабря 2013 г.

1 Понятие бинарной алгебраической операции…………………………………. 5

2 Свойства бинарной алгебраической операции…………………………………..5

Тема 2 Поле комплексных чисел………………………………………………….10

1 Алгебраическая форма комплексного числа…………………………………. 11

2 Геометрическая форма комплексного числа…………………………………. 13

3 Тригонометрическая форма комплексного числа……………………………. 14

3.1 Умножение и деление комплексных чисел, записанных в тригонометрической форме………………………………………………………..15

3.3 Извлечение корней n-ой степени из комплексного числа…………………. 15

5 Геометрическое решение уравнений……………………………………………18

Раздел 2 Матрицы и определители………………………………. 19

Тема 1 Матрицы. Определение матрицы, виды матриц, действия над матрицами.…………………………………………………….……………………19

Тема 2 Определители. Перестановки из n элементов. Подстановки n-ой степени. Определение определителя n-го порядка. Свойства определителей. Миноры и алгебраические дополнения. Теорема о разложении определителя по элементам строки или столбца. Следствие из неё……………..……………………………. 23

Тема 3 Обратная матрица. Вырожденные и невырожденные матрицы. Обратная матрица и ее вычисление. Матричные уравнения……………………………….27

Раздел 3 Системы линейных уравнений. Методы решения систем линейных уравнений…………………………………………………………………………. 29

Тема 1 Решение системы n – линейных уравнений с n неизвестными в матричном виде…………………………………………………………………….29

Тема 3 Метод последовательного исключения неизвестных (метод Гаусса). 33

Настоящие материалы составлены в соответствии с программой дисциплины «Алгебра» и предназначены для студентов направлений «Математика» и «Педагогическое образование» профиля «Математическое образование».

Разделы «Алгебры», «Поле комплексных чисел», «Матрицы и определители», «Системы линейных уравнений» изучаются в первом семестре. В данной брошюре представлены все темы раздела, которые выносятся на практические занятия. Для каждой темы указаны основные теоретические положения, приведены образцы решения типовых задач и список задач для решения.

Раздел 1 Алгебры

Тема 1 Понятие алгебры

Понятие бинарной алгебраической операции

Определение. Бинарной алгебраической операцией на множестве М называется правило (закон), по которому любым двум элементам из М, взятым в определенном порядке (т.е. паре (а,b)), ставится в соответствие единственный элемент с из этого же множества.

Пример. 1 Операция сложения на множестве чисел N, Z, Q, R.

2 Операция умножения на множестве чисел N, Z, Q, R.

Задачи для решения

1 Какие из арифметических действий (сложение, вычитание, умножение, деление) являются бинарными операциями:

б) на множестве N;

в) на множестве Z?

2 Является ли бинарной операцией:

а) умножение на множестве иррациональных чисел;

б) сложение на множестве четных чисел;

в) сложение на множестве нечетных чисел;

г) нахождение десятичных логарифмов на множестве ;

д) нахождение среднего геометрического двух чисел на множестве ;

е) нахождение наибольшего общего делителя на множестве N?

3 Являются ли действия, выполняемые по формулам:

б) a ◦ b=

в) a ◦ b =

бинарными операциями на множестве Q, и если являются, то почему?

4 Являются ли алгебраической системой множество чисел вида относительно: а) сложения; б) вычитания; в) умножения?

5 Является ли алгебраической системой множество радиусов-векторов, исходящих из начала декартовой системы координат и расположенных в первой четверти координатной плоскости, с операцией: а) сложение векторов; б) вычитание векторов?

Свойства бинарной алгебраической операции

Определение. Операция ◦ на множестве М называется коммутативной, если для любых а и b из этого множества справедливо равенство

Определение. Операция ◦ на множестве М называется ассоциативной, если для любых а, b, c M справедливо равенство

a ◦ (b ◦ c) = (a ◦ b) ◦ c.

Определение. Пусть на М задана операция ◦. Элемент е называется нейтральным относительно операции ◦, если для любого а 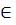М справедливо равенство

Определение. Пусть на М задана операция ◦. Элемент аʹ называется симметричным к элементу а относительно операции ◦, если выполняется равенство

а ◦ аʹ = аʹ ◦ а = е.

По сложению, аʹ обозначают –а и называют противоположным. По умножению, аʹ обозначают и называют обратным.

Определение. Пусть на М задана операция ◦. Операция ◦ называется обратимой, если для любых а, b M уравнения а ◦ x = b, y ◦ a = b имеют решение, причем единственное.

Пусть дано множество, на котором выполнимы две операции ◦ и *.

Определение. Операция ◦ называется дистрибутивной относительно операции *, если для любых a, b, c 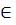M выполняются равенства

a ◦ (b*c) = (a ◦ b) *(a ◦ c),

(b*c) ◦ a = (b ◦ a) * (c ◦ a).

Пример 1 Докажем, что на множестве R бинарная операция, заданная формулой a ◦ b = коммутативна, но не ассоциативна.

Решение. Пусть a, b, c – любые действительные числа. В силу коммутативности сложения на R получим:

a ◦ b = b ◦ a,

т.е. бинарная операция нахождения среднего арифметического на R коммутативна. Далее,

(a ◦ b) ◦ c = 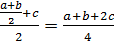(1)

a ◦ (b ◦ c) = (2)

Из результатов (1) и (2) следует, что при а ≠ с равенство (a ◦ b) ◦ c=a◦(b ◦ c) не является справедливым. Следовательно, заданная операция не ассоциативна на R.

Пример 2 Докажем, что во множестве К, содержащем не менее двух элементов, на котором формулой a ◦ b = b задана бинарная операция, не существует нейтрального элемента.

Допустим, что в К существует нейтральный элемент е, и пусть а – любой элемент из К. По определению нейтрального элемента а◦ е = а, а из условия примера следует, что а◦ е = е, т.е. а = е. Это означает, что К состоит из одного элемента. Полученный результат противоречит условию, а потому сделанное допущение ошибочно.

Задачи для решения

1 Являются ли коммутативными и ассоциативными на множестве Z бинарные операции сложения, умножения и вычитания?

2 Докажите, что на множестве бинарная операция а ◦ b = нахождения среднего геометрического коммутативна, но не ассоциативна.

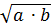
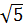
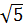
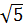
3 Обладает ли множество чисел вида а + b , где a и b – любые целые числа, нейтральным элементом относительно обычного умножения? Проверьте, имеются ли в данной алгебраической системе обратные элементы для элементов 2 + и 5 — 2 . Обратима ли на данном множестве операция умножения?

4 Какие из нижеприведенных бинарных операций:

а) a ◦ b = ;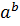

б) a ◦ b = c, где с – наибольший общий делитель чисел а и b;

в) a ◦ b = m, где m – наименьшее общее кратное чисел а и b, коммутативны и какие ассоциативны на множестве N.

5 Покажите, что действие выполняемое по правилу a ◦ b = , является коммутативной, но не ассоциативной бинарной операцией на множестве R.

6 Докажите, что относительно обычного умножения множество А= <x 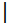x=3k, k Z> не содержит нейтрального элемента. Обратима ли операция умножения на множестве А?

7 Пусть I – множество подмножеств некоторого непустого множества М. Существует ли в I нейтральный элемент (если существует, то какой) относительно операции объединения подмножеств на I; пересечения подмножеств? Какие элементы множества I имеют симметричные относительно операций объединения и пересечения? Обратимы ли указанные операции на множестве I?

8 Докажите, что на множестве Q действие, выполняемое по правилу a◦b = = 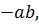является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система нейтральным элементом, и если обладает, то каким именно?

Виды алгебр

Определение. Алгеброй называется любое непустое множество А, на котором задана некоторая система операций

Обозначается (А, S), где А – множество, S – система операций.

Определение. Непустое множество М называется полугруппой, если в нем выполнима одна бинарная алгебраическая операция, которая является ассоциативной.

Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция ◦, которая обладает свойствами:

1) ◦ ( b ◦ c ) = ( ◦ b ) ◦ c,

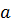
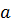
2) ◦ e = e ◦ = ;

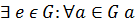
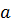
3) ◦ ʹ = ʹ ◦ = e.

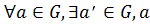
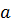
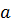
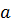
Группы по сложению называются аддитивными; группы по умножению – мультипликативными.

Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция, которая является ассоциативной и обратимой.

Определение. Если в группе G операция коммутативна, то группа G называется абелевой.

Определение. Непустое множество К называется кольцом, если в нем выполнимы две бинарные алгебраические операции – сложение и умножение, удовлетворяющие условиям:

Примеры колец. При обычных операциях сложения и умножения кольцом является множество целых чисел, множество рациональных чисел, множество действительных чисел.

Определение. Непустое множество Р называется полем, если в нем выполнимы две бинарные алгебраические операции сложение и умножение, удовлетворяющие аксиомам:

Пример 1 Доказать, что на множество Z образует группу относительно действия, заданного формулой

◦

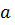
1 Рассматриваемое на Z действие сводится к сложению или вычитанию целых чисел, а т.к. сложение и вычитание элементов из Z дает в результате элемент из Z, то на множестве Z рассматриваемое действие является бинарной операцией.

2 Проанализируем возможные случаи

a) Если a, b – четные числа, а с – любое число из Z, то

◦ ◦

◦ ) ◦

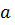
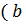
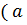
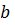
т.е. ◦ ◦ ◦ ) ◦ .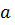

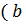
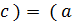
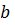
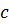
б) Если a – четное число, b – нечетное, а с – любое число из Z, то

◦ ◦

◦ ) ◦

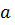
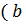
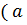
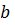
т.е. ◦ ◦ ◦ ) ◦ .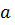

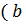
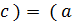
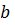
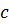
в) Если a – нечетное число, b – четное, а с – любое число из Z, то нечетно и потому

◦ ◦

◦ ) ◦

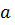
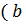
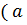
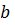
т.е. ◦ ◦ ◦ ) ◦ .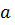

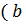
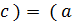
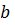
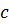
г) Если a, b – нечетные числа, а с – любое число из Z, то четно и потому

◦ ◦

◦ ) ◦

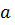
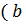
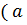
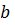
т.е. ◦ ◦ ◦ ) ◦ .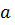

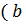
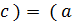
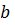
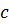
Итак, во всех возможных случаях заданная на Z бинарная операция является ассоциативной.

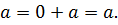
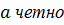
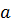
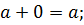
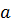
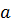
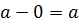
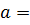
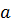
3 Т.к. 0 – четное число, то 0 ◦ Кроме того, если , то ◦ 0 = если же нечетно, то ◦ 0 = . Итак, 0 ◦ ◦ 0, т.е. 0 является в Z нейтральным элементом относительно заданной операции.

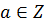
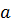
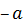
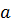
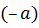
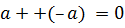
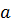
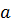
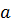
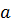
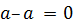
4 Для любого элемента в Z существует обратный элемент: для четного обратным будет противоположное число , т.к. ◦ = ; для нечетного обратным будет само число , т.к. ◦ = .

Итак, Z является группой относительно заданной операции.

Задачи для решения

1 Является ли множество Z полугруппой относительно: а) сложения, б) вычитания?

2 Является ли множество N полугруппой относительно операции нахождения наибольшего общего делителя?

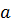
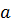
3 Почему множество R не является полугруппой относительно действия, выполняемого по правилу ◦ b = для любых , b

4 Выясните, какие из нижеприведенных множеств являются группами относительно нижеуказанных операций:

а) множество Z относительно вычитания;

б) множество четных чисел относительно умножения;

в) множество целых чисел, кратных любому заданному натуральному числу n, относительно сложения;

г) множество 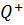относительно умножения;

д) множество Q относительно умножения;

е) множество Q относительно умножения;

ж) множество R относительно умножения;

з) множество трехмерных (n-мерных) арифметических векторов относительно сложения;

и) множество чисел вида а + b относительно сложения, если а и b – любые рациональные числа;

к) множество многочленов одной и той же степени n от одного аргумента относительно сложения;

л) множество многочленов степени не выше n относительно сложения;

м) множество многочленов от одного аргумента относительно сложения;

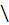
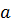
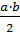
5 На множестве Q определено действие ◦ b = . Докажите, что относительно указанного действия данное множество является группой.

6 Является ли кольцом множество L чисел вида относительно обычных операций сложения и умножения?

7 Докажите, что если на Z задана операция a ʘ b = -ab, то алгебраическая система является коммутативным кольцом с единицей. Каков единичный элемент этого кольца?

8 Докажите, что множество А чисел вида 2а + 2b 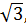где a, b – любые целые числа, является числовым кольцом.

9 Для каких чисел n = 2, 3, 4, 5, 6, 7 существует поле из n элементов?

10 Почему кольцо не является полем?

11 На множестве М = сложение 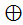и умножение определены следующим образом:

Выясните, обладает ли это множество нулем и единицей и является ли система полем относительно заданных бинарных операций.

Видео:Бинарная операция Скачать

Разрешимость и перечислимость множеств

Теперь, когда мы достаточно подробно изучили три различных формализации понятия алгоритма, установили их эквивалентность и сформулировали тезисы Тьюринга, Чёрча и Маркова, можно сделать некоторые общие выводы. Из наших рассмотрений следует, что любые утверждения о существовании или несуществовании алгоритмов, сделанные в одной из трех формализации, верны и в Другой. Это означает, что возможно развитие и изложение теории алгоритмов, инвариантное по отношению к способу формализации понятия «алгоритм». Это своего рода общая теория алгоритмов. Основные ее понятия — алгоритм и вычислимая функция.

При интерпретировании этой общей теории, например, в теории рекурсивных функций понятие алгоритм превращается в рекурсивное описание функции, понятие вычислимая функция — в понятие частично рекурсивная (или общерекурсивная) функция. (При этом следует всегда помнить, что алгоритм и вычисляемая им функция — это не одно и то же. Одна и та же функция может вычисляться с помощью разных алгоритмов.)

Будем рассматривать функции от одного или нескольких аргументов, заданные на множестве всех натуральных чисел или на некоторых его подмножествах (частичные функции) и принимающие значения в множестве . Таким образом, рассматриваются функции , являющиеся отображениями декартовой n-й степени в множество . Область определения функции есть подмножество множества — определено>. Область изменения (значений) есть подмножество множества

Определение 35.1. Функция называется вычислимой, если существует алгоритм, позволяющий вычислять ее значения для тех наборов аргументов, для которых она определена, и работающий вечно, если функция для данного набора значений аргументов не определена.

Определение 35.2. Множество называется разрешимым, если существует алгоритм , который по любому объекту дает ответ, принадлежит множеству Мили нет. Алгоритм называется разрешающим алгоритмом для .

Известно понятие характеристической функции множества . Ею называется функция , заданная на множестве , принимающая значения в двухэлементном множестве и определяемая следующим образом:

Отсюда ясно, что множество разрешимо тогда и только тогда, когда его характеристическая функция вычислима.

Примером разрешимого множества может служить множество всех тавтологий логики высказываний. Разрешающий алгоритм состоит в прямом вычислении значений данной формулы на всевозможных наборах значений ее пропозициональных переменных (составление таблицы истинности формулы).

Определение 35.3. Множество называется (рекурсивно, или эффективно, или алгоритмически) перечислимым, если либо пусто, либо есть область значений некоторой вычислимой функции или, другими словами, если существует алгоритм для последовательного порождения (перечисления) всех его элементов.

Другими словами, перечислимо, если существует такая вычислимая функция , что . Функция называется перечисляющей множество (или для множества ); соответственно алгоритм, вычисляющий , называется перечисляющим или порождающим для .

Пример 35.4. Рассмотрим множество квадратов натуральных чисел. Оно перечислимо: для получения его элементов нужно последовательно брать числа и возводить их в квадрат. Другими словами, есть область значений вычислимой функции . Более того, это множество является также и разрешимым: для проверки того, принадлежит или нет некоторое число данному множеству, нужно разложить число на простые множители, что позволит выяснить, является ли оно точным квадратом.

Далее, в теореме 35.6 будет показано, что любое разрешимое множество перечислимо, а в теореме 35.7 — что обратное утверждение неверно.

Важность понятий разрешимости и перечислимости множеств для оснований математики связана с тем, что язык теории множеств является в известном смысле универсальным языком математики. Всякому математическому утверждению можно придать вид утверждения о каких-либо множествах. В связи с этим к способам задания множеств предъявляются повышенные требования. Необходимо точное понимание таких понятий, как «конструктивный способ задания множества» и «множество, заданное эффективно». Это и достигается благодаря понятиям разрешимости и перечислимости множества. Язык разрешимых и перечислимых множеств является универсальным языком для утверждений о существовании (или отсутствии) алгоритмов решения математических проблем.

Теорема 35.5. Если множества и перечислимы, то перечислимы множества и .

Доказательство. Если имеются алгоритмы для порождения элементов множеств и , то алгоритм для порождения множества получается из исходных путем их одновременного применения. Следовательно, множество перечислимо.

Пусть теперь алгоритм последовательно порождает элементы множества , а алгоритм последовательно порождает элементы множества . Тогда алгоритм для перечисления элементов множества заключается в следующем.

Поочередно с помощью алгоритмов и порождаются элементы и т.д. Каждый вновь порожденный элемент сравнивается со всеми ранее порожденными элементами . Если совпадает с одним из них, то он включается во множество . В противном случае надо переходить к порождению элемента и сравнивать его со всеми ранее порожденными элементами , и т.д. Описанная процедура позволяет эффективно перечислить все элементы множества , что и требовалось доказать.

Теорема 35.6. Пусть . Множество разрешимо тогда и только тогда, когда оно само и его дополнение перечислимы.

Доказательство. Необходимость. Пусть — разрешимое множество. Можем считать, что , т. е. имеется элемент . Тогда характеристическая функция множества , как было отмечено выше, вычислима, т.е. имеется алгоритм для ее вычисления.

Строим алгоритм для перечисления множества . Рассмотрим функцию

Отсюда , то есть есть множество значений функции , которая, очевидно, вычислима ввиду вычислимости функции . Следовательно, множество перечислимо.

Аналогично, выбрав элемент , строим функцию:

которая также вычислима ввиду вычислимости функции . Кроме того, , т.е. есть множество значений вычислимой функции . Следовательно, множество также перечислимо.

Достаточность. Пусть множества и перечислимы, т. е. и , где и — некоторые вычислимые функции. Тогда алгоритм, выясняющий, принадлежит или нет произвольное число множеству , действует следующим образом. Последовательно порождаем элементы и на каждом шаге получаемый элемент сравниваем с . Поскольку должно принадлежать либо , либо , то на конечном шаге получим или . Если , то , а если , то и, значит, . Следовательно, множество разрешимо.

Прежде чем переходить к следующей теореме, отметим, что существует эффективное перечисление всех упорядоченных пар натуральных чисел, которое называется диагональным методом, или диагональным процессом:

Перечисление осуществляется последовательным прохождением по диагоналям, начиная с левого верхнего угла. Первыми парами этого перечисления являются:

Можно доказать, что в данной последовательности пара стоит на месте с номером

Теорема 35.7. Существует перечислимое, но неразрешимое множество натуральных чисел.

Доказательство. На основании предыдущей теоремы достаточно привести пример такого множества натуральных_чисел, которое само было бы перечислимо, а его дополнение перечислимым не было.

Ясно, что перечислимых множеств натуральных чисел (как и алгоритмов) имеется лишь счетное количество. Следовательно, все перечислимые множества можно расположить в последовательность (перенумеровать): . Более того, можно считать, что эта нумерация эффективна, т.е. по номеру множества можно восстановить само это множество.

Рассмотрим теперь алгоритм , который последовательно порождает все элементы следующего множества . На шаге с номером этот алгоритм вычисляет m-й элемент множества , и если элемент совпадает с , то он относит его в множестве . Таким образом,

Итак, порождается алгоритмом , т.е. перечислимо. Поскольку дополнение множества состоит из всех таких , что , то отличается от любого перечислимого множества хотя бы одним элементом. Поэтому не является перечислимым. Следовательно, на основании теоремы 35.6 множество неразрешимо, что и завершает доказательство.

Доказанная теорема фактически включает в себя в неявном виде теорему Гёделя о неполноте формальной арифметики, о которой мы подробно будем говорить в заключительном параграфе этой главы.

Подведем некоторые итоги. Итак, эффективно заданное множество — это множество, обладающее разрешающей или перечисляющей функцией (алгоритмом). Объединение и пересечение перечислимых множеств перечислимы. Непустое множество разрешимо тогда и только тогда, когда оно само и его дополнение перечислимы. В частности, отсюда следует, что всякое непустое разрешимое множество перечислимо. Тем не менее существует перечислимое, но неразрешимое множество натуральных чисел. В теореме 35.7 такое множество описано. Другим примером такого множества является множество определен>, т.е. множество номеров самоприменимых алгоритмов.

Таким образом, перечислимость — более слабый вид эффективности, нежели разрешимость. Хотя перечисляющая процедура и задает эффективно список элементов множества , поиск данного элемента а в этом списке может оказаться неэффективным: это неопределенно долгий процесс, который в конечном счете остановится, если , но не остановится, если . В случае же перечислимости и дополнения перечисляющая процедура для становится эффективной и гарантирует разрешимость множества .

Видео:Отношения. СвойстваСкачать

Бинарные операции и их свойства

Дата добавления: 2015-07-23 ; просмотров: 3903 ; Нарушение авторских прав

Пусть на множестве Х задано правило, которое любой паре элементов x, y из множества Х (xÎХ, yÎХ) ставит в соответствие единственный элемент z из того же множества Х (zÎХ). Такое правило называется бинарной операцией.

Для обозначения бинарной операции используется запись, при которой пары элементов соединяются специальным значком: xTy=z.

Пример. Пусть в качестве Х выступает множество действительных чисел R. Примерами операций на множестве R могут служить сложение (+), вычитание (-), умножение (·).

Свойства бинарных операций

1. Операция T называется коммутативной, если для любых элементов x,yÎХ справедливо равенство: xTy=yTx .

2. Операция T называется ассоциативной, если для любых элементов x,y,zÎХ справедливо равенство:(xTy)Tz=xT(yTz) .

Пример. Операции “+” и “·” коммутативны и ассоциативны, а операция “-” этими свойствами не обладает.

3. Операция T называется дистрибутивной относительно операции ^, если для любых элементов x, y, z Î Х справедливы равенства:

Пример. Очевидно, операция “·” дистрибутивна относительно операции “+”, “-”, причём две последние не являются дистрибутивными относительно “·”.

Элемент е называется нейтральным, или единичным, относительно операции T, если для любого xÎХ выполняются равенства: xTе = еTx = x.

Докажем, что если нейтральный элемент существует, то он единственный.

ÿ Предположим, что существуют, по крайней мере, два различных нейтральных элемента e₁¹e₂. Тогда, по определению единичного элемента, для любого xÎХ выполняются равенства:

Из двух последних равенств следует, что e₁=e₂, а это противоречит предположению. Следовательно, нейтральный элемент единственный.

Пример. Для операции “·” нейтральным элементом является 1, а для “+” — 0.

\|	следующая лекция ==>
Множество. Способы задания множеств	\|	Операции над множествами. Законы де Моргана

Не нашли то, что искали? Google вам в помощь!