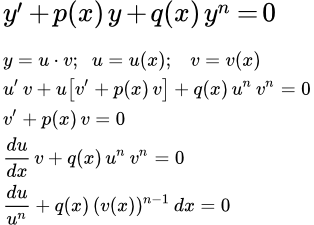Сведение уравнения бернулли к линейному

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Дифференциальные уравнения Бернулли в примерах решений

Дифференциальным уравнением Бернулли называется уравнение вида

,

Таким образом, дифференциальное уравнение Бернулли обязательно содержит функцию y в степени, отличной от нуля и единицы.

В случае, если m = 0 , уравнение является линейным, а в случае, если m = 1 , уравнение является уравнением с разделяющимися переменными.

Дифференциальное уравнение Бернулли можно решить двумя методами.

1. Переходом с помощью подстановки к линейному уравнению.
2. Методом Бернулли.

Переход от уравнения Бернулли к линейному уравнению.

Уравнение делим на :

,

.

Обозначим . Тогда , откуда . Переходя к новой переменной, получим уравнение

,

которое является линейным дифференциальным уравнение первого порядка. Его можно решить методом вариации константы Лагранжа или методом Бернулли.

Решение методом Бернулли.

Решение следует искать в виде произведения двух функций y = u ⋅ v . Подставив его в дифференциальное уравнение, получим уравнение

.

Из слагаемых, содержащих функцию u в первой степени, вынесем её за скобки:

.

Приравняв выражение в скобках нулю, то есть

,

получим дифференциальное уравнение с разделяющимися переменными для определения функции v .

Функцию u следует находить из дифференциального уравнения

,

которое также является уравнение с разделяющимися переменными.

Пример 1. Решить дифференциальное уравнение Бернулли

.

Решение. Решим дифференциальное уравнение двумя методами.

1. Переход от уравнения Бернулли к линейному уравнению. Данное уравнение умножим на y³ :

.

Введём обозначение , тогда , и приходим к уравнению

.

Решим его методом Бернулли. В последнее уравнение подставим z = u ⋅ v , z‘ = u‘v + uv‘ :

,

.

Выражение в скобках приравняем нулю и решим полученное дифференциальное уравнение:

Полученную функцию v подставим в уравнение:

2. Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v . Подставив его и y‘ = u‘v + uv‘ в данное дифференциальное уравнение, получим

Выражение в скобках приравняем нулю и определим функцию v :

Полученную функцию v подставим в уравнение и определим функцию u :

И, наконец, найдём решение данного дифференциального уравнения:

Пример 2. Решить дифференциальное уравнение Бернулли

.

Решение. Это уравнение, в котором m = −1 . Применив подстановку y = u ⋅ v , получим

Выражение в скобках приравняем нулю и определим функцию v :

Полученную функцию v подставим в уравнение и определим функцию u :

Таким образом, получаем решение данного дифференциального уравнения:

.

Пример 3. Решить дифференциальное уравнение Бернулли

.

Решение. Это уравнение можно решить, используя подстановку y = u ⋅ v . Получаем

Приравняем нулю выражение в скобках и решим полученное уравнение с разделяющимися переменными:

Подставляем v в данное уравнение и решаем полученное уравнение:

и проинтегрируем обе части уравнения:

Далее используем подстановку

:

.

Таким образом, получаем функцию u :

.

и решение данного дифференциального уравнения:

Пример 4. Решить задачу Коши для дифференциального уравнения

при условии .

Решение. Перепишем уравнение, перенося в левую сторону линейные слагаемые, а в правую — нелинейные:

.

Это уравнение Бернулли, которое можно решить, используя подстановку y = u ⋅ v , y‘ = u‘v + uv‘ :

Выражение в скобках приравняем нулю и решим дифференциальное уравнение с разделяющимися переменными:

Подставим функцию v в данное уравнение и решим полученное дифференциальное уравнение:

Вычислим каждый интеграл отдельно. Первый:

.

Второй интеграл интегрируем по частям. Введём обозначения:

Приравниваем друг другу найденные значения интегралов и находим функцию u :

Таким образом, общее решение данного дифференциального уравнения:

.

Используем начальное условие, чтобы определить значение константы:

Ищем частное решение, удовлетворяющее начальному условию:

В результате получаем следующее частное решение данного дифференциального уравнения:

.

И напоследок — пример с альтернативным обозначением производных — через дробь.

Пример 5. Решить дифференциальное уравнение Бернулли

.

Решение. Решим это уравнение первым из представленных в теоретической части методом — переходом к линейному уравнению. Разделив данное уравнение почленно на y³ , получим

.

Введём новую функцию . Тогда

.

Подставляя эти значения в уравнение, полученное на первом шаге, получим линейное уравнение:

.

Найдём его общий интеграл:

,

.

Подставляя эти значение в полученное линейное уравнение, получаем

.

Приравниваем нулю выражение в скобках:

Для определения функции u получаем уравнение

.

Интегрируем по частям:

Таким образом, общий интеграл данного уравнения

.

Видео:10. Уравнения БернуллиСкачать

Дифференциальное уравнение Бернулли и методы его решения

Видео:Уравнение Бернулли Метод БернуллиСкачать

Решение дифференциального уравнения Бернулли приведением к линейному уравнению

Рассмотрим дифференциальное уравнение Бернулли:
(1) ,
где n ≠ 0 , n ≠ 1 , p и q – функции от x .
Разделим его на y n . При y ≠ 0 или n 0 имеем:
(2) .
Это уравнение сводится к линейному с помощью замены переменной:
.
Покажем это. По правилу дифференцирования сложной функции:
;
.
Подставим в (2) и преобразуем:
;
.
Это – линейное, относительно z , дифференциальное уравнение. После его решения, при n > 0 , следует рассмотреть случай y = 0 . При n > 0 , y = 0 также является решением уравнения (1) и должно входить в ответ.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Решение методом Бернулли

Рассматриваемое уравнение (1) также можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:
y = u·v ,
где u и v – функции от x . Дифференцируем по x :
y′ = u′ v + u v′ .
Подставляем в исходное уравнение (1):
;
(3) .
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Уравнение (4) – это уравнение с разделяющимися переменными. Решаем его и находим частное решение v = v ( x ) . Подставляем частное решение в (3). Поскольку оно удовлетворяет уравнению (4), то выражение в круглых скобках обращается в нуль. Получаем:
;
.
Здесь v – уже известная функция от x . Это уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv .

Видео:Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Примеры решений дифференциального уравнения Бернулли

Пример 1

Решить уравнение
(П1.1)

Это дифференциальное уравнение Бернулли. Решаем его методом Бернулли. Ищем решение в виде произведения двух функций: . Тогда
. Подставляем в (П1.1):
;
(П1.2) .
Одну из этих функций мы можем выбрать произвольным образом. Выберем v так, чтобы выражение в круглых скобках равнялось нулю:
(П1.3) .
Тогда подставляя (П1.3) в (П1.2), мы получим дифференциальное уравнение с разделяющимися переменными:
(П1.4) .

Сначала мы определим функцию v . Нам нужно найти любое, отличное от нуля, решение уравнения (П1.3). Решаем его. Для этого разделяем переменные и интегрируем.
;
;
;
;
.
Отсюда , или . Возьмем решение с и знаком ′плюс′. Тогда , или .

Итак, мы нашли функции u и v . Находим искомую функцию y :
.
Заменим постоянную интегрирования: . Тогда общее решение исходного уравнения (П1.1) примет вид:
.

Когда мы делили на u , то предполагали, что . Теперь рассмотрим случай . Тогда . Нетрудно видеть, что постоянная функция также является решением исходного уравнения (П1.1) ⇑.

Общее решение уравнения: .
Уравнение также имеет решение .

Пример 2

На первый взгляд, кажется, что это дифференциальное уравнение не похоже на уравнение Бернулли. Если считать x независимой переменной, а y – зависимой (то есть если y – это функция от x ), то это так. Но если считать y независимой переменной, а x – зависимой, то легко увидеть, что это – уравнение Бернулли.

Итак, считаем что x является функцией от y . Подставим в исходное уравнение и умножим на :
;
;
(П2.1) .
Это – уравнение Бернулли с n = 2 . Оно отличается от рассмотренного выше, уравнения (1), только обозначением переменных ( x вместо y ). Решаем методом Бернулли. Делаем подстановку:
x = u v ,
где u и v – функции от y . Дифференцируем по y :
.
Подставим в (П2.1):
;
(П2.2) .
Ищем любую, отличную от нуля функцию v ( y ) , удовлетворяющую уравнению:
(П2.3) .
Разделяем переменные и интегрируем:
;
;
.
Поскольку нам нужно любое решение уравнения (П2.3), то положим C = 0 :
; ; .
Возьмем решение со знаком ′плюс′:
.
Подставим в (П2.2) учитывая, что выражение в скобках равно нулю (ввиду (П2.3)):
;
;
.
Разделяем переменные и интегрируем. При u ≠ 0 имеем:
;
(П2.4) ;
.
Во втором интеграле делаем подстановку :
;
.
Интегрируем по частям:
;
.
Подставляем в (П2.4):
.
Возвращаемся к переменной x :
;
;
.

Автор: Олег Одинцов . Опубликовано: 07-08-2012 Изменено: 29-10-2020

Видео:Уравнения Бернулли. Дифференциальны уравненияСкачать

Дифференциальное уравнение Бернулли

Статья раскрывает методы решения дифференциального уравнения Бернулли. В заключении будут рассмотрены решения примеров с подробным объяснением.

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Приведение к линейному уравнению 1 порядка

Дифференциальное уравнение Бернулли записывается как y ‘ + P ( x ) · y = Q ( x ) · y n . Если n = 1 , тогда его называют с разделяющими переменными. Тогда уравнение запишется как y ‘ + P ( x ) · y = Q ( x ) · y ⇔ y ‘ = Q ( x ) — P ( x ) · y .

Для того, чтобы решить такое уравнение, необходимо первоначально привести к линейному неоднородному дифференциальному уравнению 1 порядка с новой переменной вида z = y 1 — n . Проделав замену, получаем, что y = z 1 1 — n ⇒ y ‘ = 1 1 — n · z n 1 — n · z ‘ .

Отсюда вид уравнения Бернулли меняется:

y ‘ + P ( x ) · y = Q ( x ) · y n 1 1 — n · z 1 1 — n · z ‘ + P ( x ) · z 1 1 — n = Q ( x ) · z 1 1 — n z ‘ + ( 1 — n ) · P ( x ) · z = ( 1 — n ) · Q ( x )

Этот процесс вычисления и подстановки способствует приведению к линейному неоднородному дифференциальному уравнению первого порядка. В итоге проводим замену и получаем его решение.

Найти общее решение для уравнения вида y ‘ + x y = ( 1 + x ) · e — x · y 2 .

Решение

По условию имеем, что n = 2 , P ( x ) = x , Q ( x ) = ( 1 + x ) · e — x . Необходимо ввести новую переменную z = y 1 — n = y 1 — 2 = 1 y , отсюда получим, что y = 1 z ⇒ y ‘ = — z ‘ z 2 . Провести замену переменных и получить ЛНДУ первого порядка. Запишем, как

y ‘ + x y = ( 1 + x ) · e — x · y 2 — z ‘ z 2 + x z = ( 1 + x ) · e — x · 1 z 2 z ‘ — x z = — ( 1 + x ) · e — x

Следует проводить решение при помощи метода вариации произвольной постоянной.

Проводим нахождение общего решения дифференциального уравнения вида:

d z d x — x z = 0 ⇔ d z z = x d x , z ≠ 0 ∫ d z z = ∫ x d x ln z + C 1 = x 2 2 + C 2 e ln z + C 1 = e x 2 2 + C 2 z = C · e x 2 2 , C = e C 2 — C 1

Где z = 0 , тогда решение дифференциального уравнения считается z ‘ — x z = 0 , потому как тождество становится равным нулю при нулевой функции z . Данный случай записывается как z = C ( x ) · e x 2 2 , где С = 0 . Отсюда имеем, что общим решением дифференциального уравнения z ‘ — x z = 0 считается выражение z = C · e x 2 2 при С являющейся произвольной постоянной.

Необходимо варьировать переменную для того, чтобы можно было принять
z = C ( x ) · e x 2 2 как общее решение дифференциального уравнения вида z ‘ — x z = — ( 1 + x ) · e — x .

Отсюда следует, что производится подстановка вида

C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — 1 + x · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · x · e x 2 2 — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 = — ( 1 + x ) · e — x 2 2 — x C ( x ) = ∫ — ( 1 + x ) · e — x 2 2 — x d x = ∫ e — x 2 2 — x d — x 2 2 — x = e — x 2 x — x + C 3

С 3 принимает значение произвольной постоянной. Следовательно:

z = C x · e x 2 2 = e — x 2 2 — x + C 3 · e x 2 2 = e — x + C 3 · e x 2 2

Дальше производится обратная замена. Следует, что z = 1 y считается за y = 1 z = 1 e — x + C 3 · e x 2 2 .

Ответ: это решение считается решением исходного дифференциального уравнения Бернулли.

Видео:Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Представление произведением функций u ( x ) и v ( x )

Имеется другой метод решения дифференциального уравнения Бернулли, который основывается на том, что функцию представляют при помощи произведения функций u ( x ) и v ( x ) .

Тогда получаем, что y ‘ = ( u · v ) ‘ = u ‘ · v + u · v ‘ . Производим подстановку в уравнение Бернулли y ‘ + P ( x ) · y = Q ( x ) · y n и упростим выражение:

u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) · u · v n u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · u · v n

Когда в качестве функции берут ненулевое частное решение дифференциального уравнения v ‘ + P ( x ) · v = 0 , тогда придем к равенству такого вида

u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · ( u · v ) n ⇔ u ‘ · v = Q ( x ) · ( u · v ) n .

Отсюда следует определить функцию u .

Решить задачу Коши 1 + x 2 · y ‘ + y = y 2 · a r c t g x , y ( 0 ) = 1 .

Решение

Переходим к нахождению дифференциального уравнения вида 1 + x 2 · y ‘ = y · a r c t g x , которое удовлетворяет условию y ( 0 ) = 1 .

Обе части неравенства необходимо поделить на x 2 + 1 , после чего получим дифференциальное уравнение Бернулли y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

Перейдем к поиску общего решения.

Принимаем y = u · v , отсюда получаем, что y ‘ = u · v ‘ = u ‘ · v + u · v ‘ и уравнение запишем в виде

y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + u · v x 2 + 1 = u · v 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c t g x x 2 + 1

Проведем поиск частного решения с наличием разделяющих переменных v ‘ + v x 2 + 1 = 0 , отличных от нуля. Получим, что

d v v = — d x x 2 + 1 , v ≠ 0 ∫ d v v = — ∫ d x x 2 + 1 ln v + C 1 = — a r c t g x + C 2 v = C · e — a r c t g x , C = e C 2 — C 1

В качестве частного решения необходимо брать выражение вида v = e — a r c r g x . Преобразуем и получим, что

u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c r g x x 2 + 1 u ‘ · v + u · 0 = u 2 · v 2 · a r c t g x x 2 + 1 u ‘ = u 2 · v · a r c t g x x 2 + 1 u ‘ = u 2 · e — a r c t g x · a r c t g x x 2 + 1 ⇔ d u u 2 = e — a r c t g x · a r c t g x x 2 + 1 d x , u ≠ 0 ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x x 2 + 1 d x ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x d ( a r c t g x )

Имеем, что u = 0 рассматривается как решение дифференциального уравнения. Далее необходимо решить каждый из полученных интегралов по отдельности.

Интеграл с левой стороны, имеющего вид ∫ d u u 2 , необходимо найти по таблице первообразных. Получаем, что

∫ d u u 2 = — 1 u + C 3 .

Чтобы найти интеграл вида ∫ e — a r c t g x · a r c t g x d ( a r c t g x ) , принимаем значение a r c t g x = z и применяем метод интегрирования по частям. Тогда имеем, что

∫ e — a r c t g x · a r c t g x d ( a r c t g x ) = a r c t g x = z = = ∫ e — z · z d z = u 1 = z , d v 1 = e — z d z d u 1 = d z , v 1 = — e — z = = — z · e — z + ∫ e — z d z = — z · e — z — e — z + C 4 = = — e — z · ( z + 1 ) + C 4 = — e — a r c t g x · ( a r c t g x + 1 ) + C 4

— 1 u + C 3 = — e — a r c t g x · a r c t g x + 1 + C 4 1 u = e — a r c r g x · a r c t g x + 1 + C 3 — C 4 u = 1 e — a r c r g x · ( a r c t g x + 1 ) + C

Отсюда находим, что

y = u · v = e — a r c t g x e — a r c r g x · ( a r c t g x + 1 ) + C и y = 0 · v = 0 · e — a r c r g x = 0 являются решениями дифференциального уравнения Бернулли вида y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

На данном этапе следует переходить к поиску частного решения, которое удовлетворяет начальному условию. Получим, что

y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + C , тогда запись примет вид y 0 = e — a r c t g 0 e — a r c t g 0 · a r c t g 0 + 1 + C = 1 1 + C .

Очевидно, что 1 1 + C = 1 ⇔ C = 0 . Тогда искомой задачей Коши будет являться полученное уравнение вида y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + 0 = 1 a r c t g x + 1 .

📽️ Видео

Линейные дифференциальные уравнения 1 порядка. Уравнения БернуллиСкачать

Уравнения БернуллиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейные дифференциальные уравнения (Метод Бернулли)Скачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Дифференциальные уравнения Бернулли (продолжение)| poporyadku.schoolСкачать

Дифференциальные уравнения Бернулли| poporyadku.schoolСкачать

8. Дифференциальные уравнения, линейные относительно х и х'Скачать

Определяем тип ДУ 1Скачать

Уравнение БернуллиСкачать