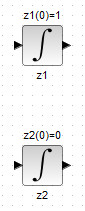Сведение дифференциального уравнения n го порядка к нормальной системе

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Сведение к системе дифференциального уравнения 2-ой степени в Xcos

Способ 2: сведение к системе в форме Коши

Рассмотрим более привычный и распространённый способ численного интегрирования обыкновенных дифференциальных уравнений n-го порядка: сведение к системе из n уравнений 1-го порядка, или, как ещё говорят, к нормальной форме или форме Коши.

Решение систем ОДУ без использования визульных блоков, было рассмотрено ранее в материале.

Рассмотрим дифференциальное уравнение второго порядка с заданными начальными условиями:

Введём замену переменных, сводящих уравнение (1) к системе из двух уравнений первой степени:

begin z_1 = y \ z_2=y’ end

получим систему в новых фазовых переменных

(2)begin z_1’=z_2\ z_2′ = -2z_2+0.3z_1\ end (3)begin z_1(0)=1\ z_2(0)=0\ end

Данную систему нам и необходимо замоделировать. Итак, разберём, какие из функциональных бликов Xcos понадобятся, чтобы найти решение задачи Коши системы из двух дифференциальных уравнений 1-ой степени (2) с начальными условиями (3).

Система (2) содержит два д.у. первого порядка, а значит нам понадобятся два блока интегратора. Здесь и в дальнейшем для моделирования дифференциальных уравнений, вместо INTEGRAL_f, будем использовать блок с палитры «Системы с непрерывным временем». Смысловая нагрузка у блока INTEGRAL_m та же, что и у используемого ранее INTEGRAL_f, — поиск первообразной сигнала, подающегося на его вход. Однако блок INTEGRAL_m во-первых, более нагляден, а во-вторых, имеет большее количество настраиваемых внутренних параметров блока.

Итак, приступим к сбору функциональной блок-схемы, реализующей поиск численного решения системы дифференциальных уравнений (2), удовлетворяющего начальным условиям (3). Для создания блок-схемы нам потребуется:

Добавить два блока INTEGRAL_m на рабочую область, дав им названия соответствующих фазовых переменных и задать во внутренних параметрах блоков INTEGRAL_m значения параметра Initial condition (начальные условия), указанные в (7б). Результатом данных действий будет схема, изображенная на рис.38;

Рисунок 38. Блоки интеграторов с заданными начальными условиями

Собирать уравнения системы (2) необходимо, начиная с последнего и двигаясь вверх. Второе уравнение системы (2) имеет вид (z_2′ = -2z_2+0.3z_1 )и представляет собой сумму двух слагаемых с разными знаками, первое из которых увеличено в 2 раза, а второе в 0.3 раз.
Поэтому нам потребуется добавить блок сумматора BIGSOM_f, во внутренних параметрах которого указан знаков слагаемых [-1;1] и блоки усилителя GAINBLK_f со значениями 2 и 3 соответственно.
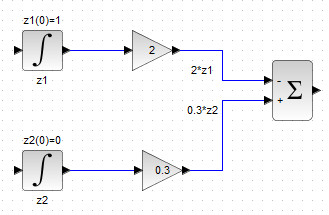
Далее необходимо составить правую част рассматриваемого уравнения, то есть подать на вход BIGSOM_f, советующие слагаемые, как показано на рис. 39.

Рисунок 39. Блок-схема правой части второго диф.уравнения системы (2)

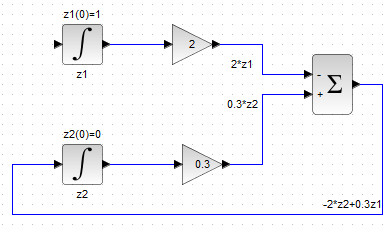
Итак, мы получили в сумматоре выражение, которые необходимо проинтегрировать, то есть подать на вход блока-интегратора INTEGRAL_m , соответствующего фазовой переменной, производная которой стоит в левой части рассматриваемого уравнения. В уравнении (z_2′ = -2z_2+0.3z_1 ) слева стоит (z_2′ ), а значит, выход сумматора нужно подсоединить ко входу интегратора, отвечающего за переменную (z_2 )(см. рис. 40).

Рисунок 40. Вывод выхода сумматора на вход интегратора

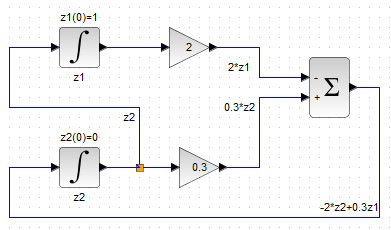
Перейдём к построению первого уравнения системы (2), имеющего вид (z_1’=z_2 ). Фазовая переменная (z_2 ) формируется как выход соответствующего блока интегратора. Распараллелим выход нижнего блока INTEGRAL_m , подав его на вход верхнего блока INTEGRAL_m , который соответствует фазовой переменной (z_1 ). В результате получим схему, изображенную на рисунке 41.

Рисунок 41. Блок-схема замкнутой системы двух д.у. 1-ой степени (2)

Далее нам потребуется вывести графики фазовых переменных (z_1, z_2 ), для этого добавьте блоки CMSCOPE, END и CLOCK_c на рабочую область.

По традиции, во внутренних параметрах блока END указать время 10сек., на функциональный вход блока CMSCOPE нужно подать выход блока CLOCK_c с параметрами Period = 0.1, Время инициализации=0, а на регулярные входы осциллографа подать распараллеленные интегральные выходы, соответствующие фазовым переменным (рис. 42).

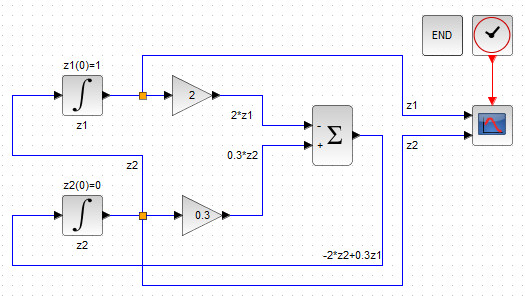
Рисунок 42. Блок-схема поиска численного задачи Коши (2-3) с выводом графиков фазовых переменных

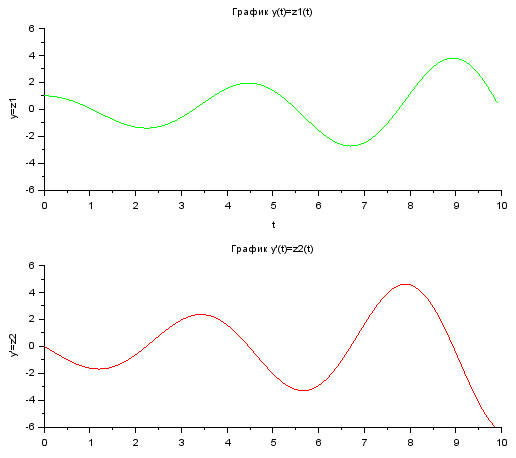
После запуска моделирования и настройки параметров осциллографа, получим графики (рис. 43).

Рисунок 43. Графическое решение задачи Коши (2-3)

Итак, основными принципами второго способа численного интегрирования дифференциальных уравнений порядка выше 1 являются:

Сведение дифференциального уравнения n-ой к системе из n уравнений 1-ой степени, путём замены переменных;

Движение снизу вверх при визуализации уравнений получившейся системы;

Параллельное включение в схему блоков INTEGRAL_m, отвечающих за фазовые переменные системы;

Отображение результата численного моделирования на системах координат фазовая переменная – время;

Задание начальных условий в соответствующих блоках-интеграторах;

Задание отрезка интегрирования во внутренних параметрах блока END, начальной точки и шага дискретизации в блоке CLOCK_c;

Возможность выбора численного метода поиска решения дифференциального уравнения в настройкам параметров интегрирования.

Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Метод исключения — сведение системы ДУ к одному уравнению

Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.

Введением новых функций

это уравнение заменяется нормальной системой уравнений

Можно утверждать и обратное, что, вообще говоря, нормальная система уравнений первого порядка

эквивалентна одному уравнению порядка . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения .

Проиллюстрируем этот метод на примере системы двух уравнений:

Здесь — постоянные коэффициенты, а и — заданные функции; и — искомые функции. Из первого уравнения системы (1) находим

Подставляя во второе уравнение системы вместо у правую часть (2), а вместо производную от правой части (2), получаем уравнение второго порядка относительно

где — постоянные. Отсюда находим . Подставив найденное выражение для и в (2), найдем .

Пример 1. Проинтегрировать систему уравнений

Решение. Из первого уравнения системы (3) находим , тогда

Подставляя (4) во второе уравнение системы (3), получаем линейное дифференциальное уравнение с постоянными коэффициентами второго порядка

Общее решение уравнения (5)

Находя производную по от (6), получаем

Общее решение системы (3):

Пример 2. Решить задачу Коши для системы

Решение. Из второго уравнения системы (7) находим

Подставляя (9) и (10) в первое уравнение системы (7), получаем уравнение , общее решение которого

Подставляя (11) в (9), найдем . Общее решение системы (7)

При начальных условиях (8) из (12) получим систему уравнений для определения

решая которую, найдем . Подставляя эти значения и в (12), получаем решение поставленной задачи Коши:

Пример 3. Решить систему уравнений

Решение. Из первого уравнения системы находим

Подставляя эти выражения для и во второе уравнение, получаем

Считая , из последнего уравнения имеем и после интегрирования получим . Теперь легко находим

Общее решение данной системы

Замечание. Не всякая система дифференциальных уравнений может быть сведена к одному уравнению более высокого порядка. Например,

не сводится к одному уравнению второго порядка. Ее общее решение .

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Сведение общей системы дифференциальных уравнений к нормальной

Здесь мы покажем, что весьма общая система дифференциальных уравнений сводится к нормальной системе и следовательно, для таких систем будет установлена теорема существования и единственности.

Сначала дадим описание общих систем дифференциальных уравнений.

В случае одной неизвестной функции x независимого переменного t дифференциальное уравнение n-го порядка имеет вид:

Здесь F — заданная функция от (n+2) переменных. Функция F, вообще говоря, может быть задана не при всех значениях своих аргументов и поэтому говорят об области D задания функции F. Предполагается обычно, что D — открытое множество евклидова пространства размерности n+2, координатами точек в котором являются переменные .

📽️ Видео

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

11. ДУ, Система ДУ. Сведение к уравнению высшего порядка. В.П. Минорский №2275Скачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Видеоурок "Линейные однородные диф. уравнения n-го порядка"Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Нефёдов Н. Н. - Дифференциальные уравнения - Задача Коши для нормальной системы ОДУ. ДУ n-го порядкаСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Лекция 8 по курсу "Дифференциальные уравнения"Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения высших порядков, допускающие понижение порядкаСкачать