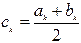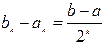Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать
Метод половинного деления. Алгоритм
Решение алгебраического уравнения. Для численного решения алгебраических уравнений существует множество способов. Среди самых известных можно назвать метод Ньютона, метод Хорд, и «всепобеждающий» метод Половинного Деления. Сразу оговоримся, что любой метод является приближенным, и по сути дела лишь уточняющим значение корня. Однако уточняющим до любой точности, заданной Нами.
Метод половинного деления или дихотомии (дихотомия — сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину. Переносится та граница, со стороны которой функция на половине отрезка знака не меняет. Далее процесс повторяется. Итерации прекращаются при выполнении одного из условий: либо длина интервала [a; b] становится меньше заданной погрешности нахождения корня ?, либо функция попадает в полосу шума ?1 — значение функции сравнимо с погрешностью расчетов.
Сначала поставим задачу. Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ?, если известно, что f(a)*f(b) Дано уравнение вида:
необходимо найти удовлетворяющие ему значения x.
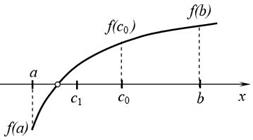
Итак, приступим к решению. Первым делом, определимся, что значит f(x)=0. Посмотрите на рис.1. На нем изображен график некоей функции. В некоторых точках этот график пересекает ось абсцисс. Координаты x этих точек нам и нужно найти. Если вид уравнения простой или стандартный, например, квадратное уравнение или линейное, то применять численный метод здесь совершенно ни к чему. Но если уравнение у нас такое:
то ни в каком учебнике вы не найдете метода аналитического решения этого кошмара. Здесь и приходит на помощь непобедимый численный метод. Метод половинного деления. Из самого названия метода можно предположить, что нам понадобится что-то делить пополам.
Ученикам метод половинного деления можно преподнести в виде решения задачи.
Идет осада неприятельской крепости. На некотором расстоянии от нее установили новую пушку. Под каким углом к горизонту надо стрелять из этой пушки, чтобы попасть в заданный участок крепостной стены.
Над моделью этой задачи физики изрядно поработали. Оно и понятно: ведь многие научные задачи, как и эта, возникали прежде всего в военном деле. И решение этих задач почти всегда считалось приоритетным.
Какие же факторы принять за существенные в этой задаче? Поскольку речь идет о средневековье, то скорость снаряда и дальность полета невелики. Значит можно считать несущественным, что Земля круглая (помните обсуждение в параграфе 27), и пренебречь сопротивлением воздуха. Остается единственный фактор — сила земного притяжения.
Математик тут бы сказал, что надо решить уравнение. Мы тоже будем решать, только приближенно и очень похоже на то, как делают настоящие артиллеристы. Они же поступают следующим образом: производят несколько выстрелов, беря цель «в вилку», т.е. одно попадание выше цели, а другое ниже. Затем делят пополам угол между этими выстрелами, и при стрельбе под таким углом снаряд ложится к цели намного ближе. Но если все же не попали, то новую «вилку» снова делят пополам и т.д.
Мы заранее можем указать «вилку» для угла: 0 и ?/4 (мы надеемся, что вы помните какой угол имеет радианную меру ?/4 и чему приближенно равно ?). А дальше будем делить пополам эту «вилку» и смотреть, куда попадает снаряд, пока не добьемся нужного результата.
Как же долго нам придется вести «пристрелку», чтобы получить угол ?, с нужной точностью? Чтобы ответить на этот вопрос, отвлечемся от нашей задачи и сформулируем на чисто математическом языке, что и как мы находили.
Нам даны некоторая функция f(x) и отрезок [a;b], причем на концах этого отрезка эта функция принимает значения противоположных знаков. Если функция непрерывна, т.е. ее график — непрерывная линия, то ясно, что график функции пересекает ось абцисс в некоторой точке с отрезка [a;b], как показано на рисунке 1. Иными словами, f(c)=0, т.е. с — корень уравнения f(x)=0.
Как же предлагается находить этот корень? А вот так. Делим отрезок [a;b] пополам, т.е. берем середину отрезка а+b/2. В этой точке вычисляем значение функции f(x) (рис. 2). Если это значение 0, то корень найден; если нет, то оно имеет тот же знак, что и значение на одном из концов отрезка [a;b]. Тогда этот конец заменям точкой а+b/2. Новый отрезок тоже содержит корень уравнения f(x)=0, поскольку на его концах функция f(x) снова имеет разные знаки. Однако этот отрезок в 2 раза короче предыдущего. И самое главное — с ним можно поступить точно так же. со следующим отрезком еще раз проделать то же самое и т.д. поскольку длина отрезка каждый раз уменьшается вдвое, мы можем получить отрезок сколь угодно малой длины, внутри которого содержится корень уравнения f(x)=0. Например, если исходный отрезок был [3;4], т.е. имел длину 1, то через десять шагов мы получим отрезок длиной. Это означает, что концы отрезка дают нам приближенное значение корня с точностью, равной длине отрезка: левый конец отрезка — приближенное значение корня с недостатком, правый конец — приближенное значение корня с избытком.
Фактически мы сейчас сформулировали метод приближенного решения уравнения f(x)=0. Его можно было бы назвать методом артиллерийской пристрелки. Но математики называют его методом половинного деления.
Далее ученикам предлагается записать алгоритм и блок-схему нахождения корня уравнения с помощью метода половинного деления.
1) Найдем середину отрезка [a; b]: c=(a+b)/2;
2) Вычислим значения функции в точках a и c и найдем произведение полученных значений: d=f(c)?f(a);
3) Если d>0, то теперь точкой a станет c: a=c; Если d ?, то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;
Видео:Метод половинного деления. ДихотомияСкачать
Двоичный поиск. Метод половинного деления
Двоичный поиск. Метод половинного деления.
Решать уравнения нас учат на уроках алгебры. Для разных типов уравнений применяются разные методы. Все они дают точные решения и все относятся к так называемым аналитическим методам. Мы знаем аналитические решения для уравнений первой и второй степени. В тех случаях, когда удается выполнить разложение на множители, нам удается аналитически решить уравнения третьей и четвертой степеней, но что мы будем делать с уравнением пятой степени, если оно на множители не раскладывается?
Когда в задаче возникают такие уравнения, их решают численными методами. Численные методы позволяют получить не точное, а приближенное решение уравнения, но с любой точностью, которую только может обеспечить компьютер.
Большинство численных методов решения уравнений являются итерационными. Это означает, что отдельный шаг (или итерация) алгоритма позволят получить лишь очередное приближение к значению корня, однако каждая последующая итерация позволяет получить все более и более точные значения корня, пока требуемая точность не будет достигнута.
Для учащихся предлагается данная теория, однако в более преемственной форме.
В начале урока ставиться цель ознакомиться с двоичным поиском и узнать, как можно решить любое уравнение. При этом сразу предупреждаем, что никаких формул не будет, а речь наша о том, как решать уравнения с помощью компьютера без всяких формул.
Предлагается игра “Угадай – ка”. Вот ее условия:
Учащиеся задумывают натуральное число от 1 до 16 (число записывают на листок и передают одноклассникам для ознакомления), а учитель задавая не более 4 вопросов, отгадывает задуманное число. При этом на вопросы учителя учащиеся отвечают только “да” или “нет”. Например, задумано число 15.
Происходит диалог следующего вида:
Учитель спрашивает: 1. Задуманное число больше 8? Ответ учеников: Да.
Учитель спрашивает: 2. Задуманное число больше 12? Ответ учеников: Да.
Учитель спрашивает: 3. Задуманное число больше 14? Ответ учеников: Да.
Учитель спрашивает: 4. Задуманное число больше 15? Ответ учеников: Нет.
Учитель отвечает: Это число 15.
Такую игру проигрывают 3 раза, тем самым убеждают учащихся, что совпадений нет, а есть точный алгоритм угадывания. Предлагается проанализировать следующие вопросы:
1. Как учитель угадывает задуманное число?
2. Почему гарантировано угадывание числа за 4 вопроса?
1. Тот промежуток чисел, в котором находится задуманное число, следует разделить пополам и выяснить в какой половине находится это число. С уменьшенным вдвое промежутком опять поступить так же, то есть, как сказали бы артиллеристы, взять искомое число в “вилку” до полного “попадания в цель”
Откуда же видно, что для этого достаточно четырёх вопросов?
2. Дело в том, что четырёхкратное деление пополам промежутка чисел от 1 до 16 приведёт к промежутку, состоящему только из двух чисел: 1 и 2. Удвоим его. Получим промежуток чисел от 1 до 4. Снова удвоим и так далее, пока верхняя граница не достигнет 2 4 =16, которая, как видите, включает наш промежуток. То есть мы должны брать ту степень числа 2, при которой наш промежуток будет полностью включаться, либо быть равным, либо меньшим.
Для лучшего восприятия посмотрите (рис.1), где красные линии – это ответ “Да”, черные – ответ “Нет”. При каждом делении промежутка на 2 существует верхняя граница N, которая звучит в вопросе: “Это число больше N ?”
Метод, который мы сейчас разобрали для отгадывания задуманного числа, называют двоичным поиском. Он применим к отысканию элемента в любом множестве, элементы которого упорядочены по отношению к какому – либо свойству.
Например: смотрим (рис. 2)
Можно знакомясь с человеком, угадывать его имя: сначала спросить про первую букву, расположена ли она в алфавите после буквы “П” , получив ответ, разделить соответствующую часть алфавита еще пополам и задать следующий вопрос о первой букве и так далее. Когда первая буква будет отгадана, начать отгадывать вторую. К концу этого процесса скорее всего, будете чувствовать себя старыми знакомыми, слегка поднадоевшими друг другу.
По данному примеру можно предложить написать алгоритм угадывания имени человека по буквам и обсудить вопросы, почему в данном случае можно применить двоичный поиск .
Устно решим задачу:
Сейчас открыто 110 химических элементов. На викторине по химии ведущий загадывал один из элементов, а участнику разрешалось задать последовательно 8 вопросов об этом элементе, на которые ведущий отвечал только “да” или “нет”, после чего участник должен назвать загаданный элемент. Зашедший на эту викторину программист – профессионал сказал, что если ему дадут таблицу Менделеева (так как он не помнит названий всех 110 элементов), то он обойдется 7 вопросами. Какие 7 вопросов вы могли бы предложить?
Алгоритм решения выглядит следующим образом. Воспользуемся таблицей Менделеева (рис.3) и зададим вопросы:
- Этот элемент расположен по порядку возрастания порядкового номера правее 55 элемента? (110:2=55)
- В зависимости от ответа, если “да”: элемент расположен правее 82 элемента?
Если “нет”: элемент расположен правее 28 элемента?
Вопрос: Как программист определил наименьшее количество задаваемых вопросов?
Ответ: 2 7 = 128, если 110 семь раз делить на 2, то получим всего два числа 1 и 2, то есть угадать будет легко.
Для выявления уровня способностей экспериментатор предлагает обучаемому тест, состоящий из 16 задач, расположенных в порядке возрастания сложности. Метод решения первой задачи экспериментатор объясняет сам, а затем предлагает обучаемому решить самую трудную, 16–ю задачу. Если обучаемый с ней справится, то экспериментатор предложит решить 15–ю; если не справится с 15–й , будет предложена 14–я и так далее, пока не обнаружится задача, которую обучаемый сможет решить. Её номер и показывает уровень способностей обучаемого. Вообще говоря, может случиться так, что обучаемому придется предложить решать все 15 задач. Заглянувший к экспериментатору профессиональный программист сказал, что уровень способностей можно выявить, предложив решить не более четырех задач. Объясните почему и как для этого надо организовать эксперимент.
Решение: Сначала необходимо уточнить, что промежуток от 2 до 16 (первая задача решена экспериментатором).
- Предложить сначала решить 9 задачу;
- если справился с 9–ой, то решать 13 – ю,
иначе 5 – ю; - И так далее.
Можно изобразить рисунок, облегчающий понимание. (рис. 4)
Теперь на данном этапе учащиеся готовы вернуться к задаче, с которой начали этот урок – решение любого уравнения с помощью компьютера.
Посмотрите на график функции.(рис. 5)
Возьмем какую – либо точку на отрезке [a;b] расположенную левее корня (напомним, что корнем функции называется значение аргумента при котором функция обращается в ноль). В этой точке значение функции отрицательно и это сигнализирует нам, что искомый корень больше выбранного нами числа.
Если же взять точку правее корня, то значение функции в ней будет положительно и это сигнализирует нам, что искомый корень меньше выбранного нами числа.
Получается очень похоже на игру “Угадай — ка”, только угадать надо число являющееся корнем уравнения.
Для этого прежде всего возьмем корень в “вилку”, то есть отрезок [a;b] так, чтобы значение функции на его концах было разных знаков. Если непрерывная функция на отрезке меняет знак, то она имеет на этом отрезке хотя бы один корень. Затем найдем середину отрезка.
Вопрос: Как найти середину отрезка ?
Если в ней функция отрицательна, то дальше надо угадывать корень на правой половине отрезка; если положительна, то на левой и так далее.
Такой метод нахождения корня называют уже не двоичным поиском, а методом деления пополам.
Итак, выбирая середину отрезка, мы не можем ожидать, что сразу попадём на корень функции. Фактически мы каждый раз лишь уменьшаем вдвое отрезок, на котором наверняка имеется корень. Постепенно этот отрезок, станет настолько малым, что любой из его концов можно считать приближённым значением корня с нужной точностью.
На практике почти все измерения производятся лишь с определённой точностью Е.
Важно отметить, что метод деления пополам годится лишь в том случае, если функция f (x) непрерывна (то есть изображается на графике непрерывной линией), а на концах исходного отрезка [a; b] функция принимает значения разных знаков. Если непрерывная функция на отрезке меняет знак, то она на этом отрезке имеет по крайней мере один ноль.
Составим блок-схему (метода деления пополам) (рис. 6)
А теперь решим задачу
Уравнение y=3cos(2x+4) имеет единственный корень на отрезке [1;3]. Решим это уравнение с точностью до 0,001 методом половинного деления на ЭВМ
Переведем блок-схему на язык программирования.
DEFFN F(X)= 3*COS(2*X+4)
INPUT A,B,E
10 C=(A+B)/2
IF FN F(C)=0 THEN A=C: B=C: GOTO 20
IF FN F(A)* FN F(C) E THEN 10
X=(A-B)/2
PRINT X
END
Label 1, 2;
Var a, b, e, c, x :real;
Function fx (y :real) :real;
Begin
Fx : =3*cos(2*y+4);
End;
Begin
Writeln(‘введи a, b, e’);
Readln(a, b, e);
1: c:=(a+b)/2; writeln(с);
if fx(c) =0 then Begin a:=c; b:=c; goto 2; end;
if fx(c)*fx(a) e then goto 1;
x: = (a+b)/2;
writeln(x);
2
1.5
1.75
1.875
1.9375
1.90625
1.921875
1.9296875
1.92578125
1.927734375
1.9267578125
1.92724609375
Последний результат можно считать значением корня с точностью Е.
Изменив функцию в данной программе, можно применять тот же метод для решения других уравнений, например x – cos(x) = 0; x – ln(x+2) = 0 на промежутке [0;1] и тому подобное. Попробуйте поэкспериментировать с разными функциями и разными начальными значениями. “Охота” за корнями уравнения очень увлекательное занятие.
Видео:Метод половинного деления решение нелинейного уравненияСкачать
Метод половинного деления
Считаем, что отделение корней уравнения f ( x) = 0 проведено и на отрезке [ a, b] расположен один корень, который необходимо уточнить с погрешностью ε. В качестве начального приближения корня принимаем середину этого отрезка: c0 = (a + b) / 2 (рис. 4):
Рис. 4. Метод половинного деления.
Затем исследуем значение функции f ( x) на концах отрезков [ a, c0 ] и [ c0 , b] . Тот из отрезков, на концах которого f ( x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка [ a1 , b1 ] (на рис. 4 это отрезок [ a, c0 ]). Вторую половину отрезка [ a, b], на которой f ( x) не меняет знак, отбрасываем. В качестве следующего приближения корня принимаем середину нового отрезка
c1 = ( a1 + b1 ) / 2 и т.д. Таким образом, k-е приближение вычисляется как
После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций в 2 k раз:
Прекратить итерационный процесс следует, когда будет достигнута заданная точность, т.е. при выполнении условия |x0 – ck|
Дата добавления: 2017-09-19 ; просмотров: 3771 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
💡 Видео
6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать
8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать
12й класс; Информатика; "Численные методы. Метод половинного деления"Скачать
Метод половинного деления - ВизуализацияСкачать
Метод половинного деленияСкачать
Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать
Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать
Урок 10. C++ Метод половинного деленияСкачать
Метод дихотомииСкачать
Метод дихотомии c++Скачать
Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать
Метод Ньютона (метод касательных) Пример РешенияСкачать
Решение нелинейного уравнения методом деления отрезка пополамСкачать
1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать
Метод простых итераций пример решения нелинейных уравненийСкачать
Решение уравнений (метод дихотомии) на C#Скачать
