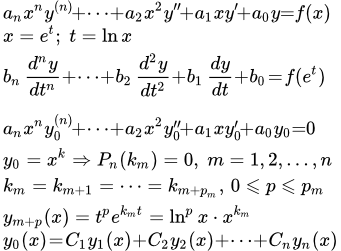Суть метод эйлера решения дифференциальных уравнений

Метод Эйлера: для чего он нужен, порядок действий и упражнения — Наука

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Содержание:

В Метод Эйлера Это самая базовая и простая из процедур, используемых для нахождения приближенных численных решений обыкновенного дифференциального уравнения первого порядка, при условии, что известно его начальное условие.

Обыкновенное дифференциальное уравнение (ОДУ) — это уравнение, которое связывает неизвестную функцию одной независимой переменной с ее производными.

Если наибольшая производная, которая появляется в уравнении, имеет степень один, то это обыкновенное дифференциальное уравнение первой степени.

Самый общий способ написать уравнение первой степени:

Видео:Метод ЭйлераСкачать

Что такое метод Эйлера?

Идея метода Эйлера заключается в нахождении численного решения дифференциального уравнения в интервале между X₀ и X_F .

Сначала интервал дискретизируется на n + 1 балл:

Которые получаются так:
Икс_я= х₀+ я

Где h — ширина или шаг подынтервалов:

С начальным условием также можно узнать производную в начале:

Эта производная представляет собой наклон касательной к кривой функции y (x) точно в точке:

Затем делается приблизительный прогноз значения функции y (x) в следующей точке:

Затем была получена следующая приближенная точка решения, которая будет соответствовать:

Процедура повторяется для получения последовательных баллов.

На рисунке, показанном в начале, синяя кривая представляет точное решение дифференциального уравнения, а красная — последовательные приближенные точки, полученные с помощью процедуры Эйлера.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Решенные упражнения

Видео:Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Упражнение 1

я) Пусть дифференциальное уравнение имеет вид:

При начальном условии x = a = 0; Y_к= 1

Используя метод Эйлера, получить приближенное решение Y в координате X = b = 0,5, разбивая интервал [a, b] на n = 5 частей.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Решение

Численные результаты резюмируются следующим образом:

Из чего делается вывод, что решение Y для значения 0,5 составляет 1,4851.

Примечание: для проведения расчетов, Smath studio, бесплатная программа для бесплатного использования.

Видео:Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

Упражнение 2.

II) Продолжая работу с дифференциальным уравнением из упражнения I), найдите точное решение и сравните его с результатом, полученным методом Эйлера. Найдите ошибку или разницу между точным и приблизительным результатом.

Видео:Метод Эйлера. Решение систем ДУСкачать

Решение

Точное решение найти не очень сложно. Производная функции sin (x) известна как функция cos (x). Следовательно, решение y (x) будет:

Для выполнения начального условия и (0) = 1 константа C должна быть равна 1. Затем точный результат сравнивается с приблизительным:

Сделан вывод, что в расчетном интервале аппроксимация имеет три значащих цифры точности.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Упражнение 3.

III) Рассмотрим дифференциальное уравнение и его начальные условия, указанные ниже:

При начальном условии x₀ = 0; Y₀ = 1

Используйте метод Эйлера, чтобы найти приблизительные значения решения у (х) в интервале х = [0, 1,5]. Используйте шаг h = 0,1.

Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Решение

Метод Эйлера очень подходит для использования с электронной таблицей. В этом случае мы будем использовать электронную таблицу геогебра бесплатная и бесплатная программа.

В электронной таблице на рисунке показаны три столбца (A, B, C), первый — это переменная Икс , второй столбец представляет переменную Y, а третий столбец — производная Y ‘.

Строка 2 содержит начальные значения Икс, Y, Y ‘ .

Шаг значения 0,1 помещен в ячейку абсолютного положения ($ D $ 4).

Начальное значение y0 находится в ячейке B2, а y1 — в ячейке B3. Чтобы вычислить y₁ используется формула:

Эта формула электронной таблицы будет иметь вид B3: = B2 + $ D $ 4 * C3.

Точно так же y2 будет в ячейке B4, и его формула показана на следующем рисунке:

На рисунке также показан график точного решения и точки A, B,…, P приближенного решения по методу Эйлера.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Ньютоновская динамика и метод Эйлера

Классическая динамика была разработана Исааком Ньютоном (1643 — 1727). Первоначальная мотивация Леонарда Эйлера (1707 — 1783) к разработке своего метода заключалась именно в решении уравнения второго закона Ньютона в различных физических ситуациях.

Второй закон Ньютона обычно выражается в виде дифференциального уравнения второй степени:

куда Икс представляет положение объекта в момент т. Указанный объект имеет массу м и подвергается силе F. Функция F связана с силой и массой следующим образом:

Для применения метода Эйлера требуются начальные значения времени. т, скорость v и положение Икс.

В следующей таблице объясняется, как, начиная с начальных значений t1, v1, x1, можно получить приближение скорости v2 и положения x2 в момент t2 = t1 + Δt, где Δt представляет небольшое увеличение и соответствует шагу в методе Эйлер.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать

Упражнение 4.

IV) Одна из фундаментальных проблем механики — это проблема блока массы M, привязанного к пружине (или пружине) с постоянной упругостью K.

Второй закон Ньютона для этой проблемы будет выглядеть так:

В этом примере для простоты мы возьмем M = 1 и K = 1. Найдите приблизительные решения для положения Икс и скорость v методом Эйлера на временном интервале [0, π / 2], разбивая интервал на 12 частей.

Возьмите 0 в качестве начального момента, начальную скорость 0 и начальное положение 1.

Видео:Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Решение

Численные результаты представлены в следующей таблице:

Также отображаются графики положения и скорости между временами от 0 до 1,44.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Предлагаемые упражнения для дома

Видео:Системы дифференциальных уравнений.Метод исключения.Метод Эйлера.Скачать

Упражнение 1

Используйте электронную таблицу, чтобы найти приближенное решение с помощью метода Эйлера для дифференциального уравнения:

y ’= — Exp (-y) с начальными условиями x = 0, y = -1 в интервале x = [0, 1]

Начните с шага 0,1. Постройте результат.

Видео:Численные методы решения ДУ: метод ЭйлераСкачать

Упражнение 2.

Используя электронную таблицу, найдите численные решения следующего квадратного уравнения, где y является функцией независимой переменной t.

y ’’ = -1 / y² с начальным условием t = 0; и (0) = 0,5; у ‘(0) = 0

Найдите решение на интервале [0,5; 1.0] с шагом 0,05.

Постройте результат: y vs t; y ‘vs t

Видео:метод Эйлера для решения ОДУСкачать

Ссылки

1. Метод Эрлера Взято с wikipedia.org
2. Решатель Эйлера. Взято с en.smath.com

50 отличных фраз аниме (вдохновляющих и запоминающихся)

Тетраплегия: характеристики, симптомы, виды и лечение

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ begin tag frac &= f_i (t, u_1, u_2, ldots, u_n), quad t > 0\ tag u_i(0) &= u_i^0, quad i = 1, 2, ldots, m. end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ begin tag frac<d pmb> &= pmb(t, pmb), quad t > 0, \ tag pmb(0) &= pmb_0 end $$ В задаче Коши необходимо по известному решению в точке ( t = 0 ) необходимо найти из уравнения (3) решение при других ( t ).

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной ( t ) (время) из ( N_t + 1 ) точки ( t_0 ), ( t_1 ), ( ldots ), ( t_ ). Нужно найти значения неизвестной функции ( pmb ) в узлах сетки ( t_n ). Обозначим через ( pmb^n ) приближенное значение ( pmb(t_n) ).

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения ( pmb^ ) на основе предыдущих вычисленных значений ( pmb^k ), ( k 0 ) при ( tauto 0 ).

Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Системы дифференциальных уравненийСкачать

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами ( t_n ) и ( t_ ): $$ omega_tau = . $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ pmb^prime (t_n) = pmb(t_n, u(t_n)), quad t_n in omega_tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ pmb^prime(t) = lim_ frac<pmb(t+tau) — pmb(t)>. $$

В произвольном узле сетки ( t_n ) это определение можно переписать в виде: $$ begin pmb^prime(t_n) = lim_ frac<pmb(t_n+tau) — pmb(t_n)>. end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг ( tau ), который даст численное приближение ( u^prime(t_n) ): $$ begin pmb^prime(t_n) approx frac<pmb^ — pmb^>. end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по ( tau ), т.е. ( O(tau) ). Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_n, pmb^). end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение ( y^n ) для того, чтобы решить уравнение (5) относительно ( y^ ) и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое ( t_ ): $$ begin tag pmb^ = pmb^n + tau pmb(t_n, pmb^) end $$

При условии, что у нас известно начальное значение ( pmb^0 = pmb_0 ), мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины ( m+1 ) (( m ) — размерность задачи), а функция F должна возвращать numpy -массив размерности ( m+1 ), t[n] — значение в момент времени ( t_n ).

Таким образом численное решение на отрезке ( [0, T] ) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции ( F ) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_, pmb^). end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое ( t_ ) нужно решить нелинейное уравнение относительно ( pmb^ ): $$ begin tag pmb^ — tau pmb(t_, pmb^) — y^n = 0. end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ begin tag frac<pmb^ — pmb^n> = sum_^s b_i pmb_i, end $$ где $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^s a_pmb_j right), quad i = 1, 2, ldots, s. end $$ Формула (9) основана на ( s ) вычислениях функции ( pmb ) и называется ( s )-стадийной. Если ( a_ = 0 ) при ( j geq i ) имеем явный метод Рунге—Кутта. Если ( a_ = 0 ) при ( j > i ) и ( a_ ne 0 ), то ( pmb_i ) определяется неявно из уравнения $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^ a_pmb_j + tau a_ pmb_i right), quad i = 1, 2, ldots, s. end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ begin tag pmb_1 & = pmb(t_n, pmb^n), &quad pmb_2 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_1> right),\ pmb_3 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_2> right), &quad pmb_4 &= pmbleft( t_n + tau, pmb^n + tau pmb_3 right),\ frac<pmb^ -pmb^n> &= frac (pmb_1 + 2pmb_2 + 2pmb_3 + pmb_4) & & end $$

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах ( pmb^n ) и ( pmb^ ) — один шаг по переменной ( t ). Линейный ( m )-шаговый разностный метод записывается в виде $$ begin tag frac sum_^m a_i pmb^ = sum_^ b_i pmb(t_, pmb^), quad n = m-1, m, ldots end $$ Вариант численного метода определяется заданием коэффициентов ( a_i ), ( b_i ), ( i = 0, 1, ldots, m ), причем ( a_0 ne 0 ). Для начала расчетов по рекуррентной формуле (13) необходимо задать ( m ) начальных значений ( pmb^0 ), ( pmb^1 ), ( dots ), ( pmb^ ) (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ begin tag pmb(t_) — pmb(t_n) = int_^<t_> pmb(t, pmb) dt end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции ( pmb^ = pmb(t_, pmb^) ), ( pmb^n ), ( dots ), ( pmb^ ), т.е. $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен ( m+1 ).

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям ( pmb^n ), ( pmb^ ), ( dots ), ( pmb^ ) и поэтому $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет ( m )-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ frac<pmb^ — pmb^n> = frac (23 pmb^ -16pmb^ + 5pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ frac<pmb^ — pmb^n> = frac (9pmb^ + 19pmb^ — 5pmb^ + pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке ( u = w ) передаются линейной системой $$ begin frac