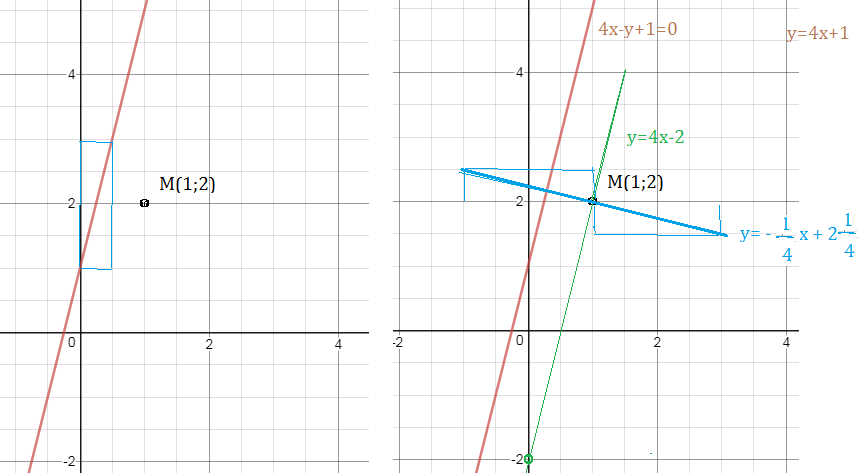
Условие
Пусть прямая l1(4x–y+1=0) одна из сторон квадрата, а точка M(1;2) его вершина. Составить уравнение остальных сторон квадрата
Решение
Расстояние d от точки M(1;2) до прямой 4х-у+1=0
это длина стороны квадрата
Уравнение прямой 4x-y+1=0 можно записать
y=4x+1
k=4
k=tg α ;
Значит прямая c угловым коэффициентом 4 — это диагональ прямоугольника, размеры 1 × 4 ( длина 1, высота 4: tgα=4/1)
Параллельная ей прямая проходит через точку М
k=4
y=4x+m
Чтобы найти m подставляем координаты точки M
2=4*1+m
m=-2
Перпендикулярная ей прямая имеет угловой k=-1/4
(потому что произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1))
Чтобы найти b подставляем координаты точки M
2=(-1/4)*1+b
b=2 целых 1/4
[b]y=(-1/4)x + 2 целых 1/4⇒ 4y+x-9=0[/b]
Третья сторона имеет угловой коэффициент k=(-1/4) и находится на расстоянии 3/sqrt(17) от точки M (1;2)
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
9-4n=-3 или 9-4n=3
n=3 или n=3/2
[b]4y+x-12 =0[/b] или [b]4y+x-6=0[/b]
О т в е т. [b]y=4x-2[/b]; [b]4y+x-9=0[/b]; [b]4y+x-12 =0[/b] (или [b] 4y+x-6=0[/b]) 
Аналитическая геометрия Индивидуальные задания и методические указания по выполнению модуля (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 |
Две стороны треугольника заданы уравнениями 2x + y – 1 = 0 и x – 3y + 14 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение третьей стороны
Даны уравнения сторон треугольника: (АВ) 7x – 2y + 32 = 0; (АС) x + y + 2 = 0; (ВС) 4x + y + 1 = 0. Найти точку пересечения его высот
Составьте уравнения катетов прямоугольного равнобедренного треугольника, если уравнение гипотенузы 3x – y + 11 = 0 и С(4;3) – вершина прямого угла
В равнобедренном треугольнике известны: уравнение основания 5x + 3y – 53 = 0, уравнение одной из боковых сторон x + 4y – 14 = 0 и точка на второй боковой стороне (3;7). Найдите уравнение второй боковой стороны
Одна из сторон квадрата лежит на прямой x – 5y + 32 = 0, а одна из вершин находится в точке (8;1). Найдите уравнения остальных сторон квадрата
Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 4x – 7y + 28 = 0, концы которого лежат на осях координат
Точки К(1;3) и L(-1;1) являются серединами оснований равнобедренной трапеции, а точки Р(3;0) и Q(-3;5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции
Даны стороны треугольника: (АС) 2x – 15y – 55 = 0; (AB) 4x – 3y + 25 = 0; (BC) 14x + 3y – 61 = 0. Составить уравнение прямой, проходящей через вершину С и через точку на стороне АВ, делящую ее (считая от вершины А) в отношении 1:4
Точки В(7;1) и D(9; -3) являются противоположными вершинами квадрата. Определить координаты двух других вершин
Видео:Уравнения стороны треугольника и медианыСкачать
В треугольнике известны уравнения высоты x + y – 3 = 0 и медианы 11x – 4y + 10 = 0, проведенных из различных вершин. Написать уравнения сторон треугольника, зная одну его вершину (8;9).
Написать уравнение сторон треугольника, зная одну его вершину (6;3), уравнения высоты 11x – 9y + 75 = 0 и биссектрисы 11x – 13y + 79 = 0, проведенных из одной вершины
Точка А(2;0) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой x + y – 1 =0. Составить уравнения двух других сторон
Длина стороны ромба с острым углом 60° равна 2. Диагонали ромба пересекаются в точке М(1;2), причем большая диагональ параллельна оси абсцисс. Составить уравнения сторон ромба
Точка А(1;2) является серединой одного из оснований прямоугольной трапеции, а точка В(3; -1) – серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x – 3y + 10 = 0. Составить уравнения остальных сторон трапеции
Написать уравнения сторон треугольника, зная одну его вершину (9;2), уравнения биссектрисы x + y – 5 =0 и медианы x – y = 0, проведенных из различных вершин
Даны координаты двух вершин треугольника А(-1;3), В(2;5) и ортоцентр – точка Н(1;4). Найти координаты третьей вершины треугольника. (Ортоцентром треугольника называется точка пересечения его высот)
Точка Н(-3;2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых 2x – y = 0 и x + y – 3 =0. Составить уравнение третьей стороны
Найти радиус и координаты центра окружности, проходящей через точку А(-1;3) и касающейся прямых 7x + y = 0 и x – y + 8 = 0
Окружность проходит через точки М(1;0) и N(2;1). Найдите центр этой окружности, если известно, что он лежит на прямой 5x – y – 4 = 0
Видео:найти уравнения биссектрис углов между прямымиСкачать
Точки В(1;2) и С(3; -6) симметричны относительно некоторой прямой. Составить уравнение этой прямой
Диагонали параллелограмма пересекаются в точке К(-2;4). Составить уравнение диагонали, не проходящую через точку пересечения сторон 4x – y + 4 = 0 и 4x +3y +20 = 0
Площадь прямоугольного треугольника, катетами которого являются оси координат, равна 8. Составить уравнение гипотенузы, если известно, что она проходит через точку А (-4;8)
Составить уравнение прямой L1, параллельной прямой L2: 2x + 3y – 23 = 0, если середина отрезка прямой L3: 5x +2y +3 = 0, заключенного между параллельными прямыми L1 и L2 лежит на прямой L4: 5x – y + 24 = 0
Составить уравнение стороны треугольника, в котором известны точка пересечения медиан (-1;7) и уравнения двух других сторон x + 4y – 37 = 0; 2x – y + 16 = 0
Даны две стороны x – y + 5 = 0 и x – y + 10 = 0 и диагональ 3x + y – 10 = 0 ромба. Найти вершины ромба
В треугольнике известны две вершины А(-2;9), В(2; -3) и точка пересечения высот О(2;7). Написать уравнения сторон
Точка А(3; -2) является вершиной квадрата, а точка М(1;1) – точкой пересечения его диагоналей. Составить уравнения сторон квадрата
Даны уравнения одной из сторон ромба x + y – 39 = 0 и одной из его диагоналей x – 3y + 11 = 0. Найти уравнения остальных сторон ромба
Найти координаты вершин параллелограмма, в котором известны две стороны 2x – 5y – 5 = 0 и 2x + 5y – 15 = 0 и диагональ 6x + 5y – 35 = 0
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Найти координаты точек С и D четырехугольника ABCD, в котором отрезки АВ и DC параллельны, BD и АС перпендикулярны друг другу и заданы вершины А(9; -1), В(5;5)
Даны две вершины (3; -1), (1;4) и центр тяжести (0;2) треугольника. Найти координаты третьей вершины треугольника и составить уравнения его сторон
Даны уравнения двух высот треугольника 3x + 4y – 23 = 0 и 12x – 5y – 24 = 0 и одна из его вершин (1;1). Составить уравнения сторон
Написать уравнения сторон треугольника, две медианы которого лежат на прямых x + y – 3 = 0 и 2x + 3y – 1 = 0, а точка А(1;1) является вершиной треугольника
Две стороны треугольника заданы уравнениями, x + 3y – 21 = 0 и 7x + y + 13 = 0, а середина третьей стороны – точка (2;3). Составить уравнение третьей стороны
Даны уравнения сторон треугольника: (MN) 3x – 5y + 17 = 0, (NP) 8x + 6y – 32 = 0, (МР) 5x + 11y + 9 = 0. Найти ортоцентр треугольника. (Ортоцентром треугольника называется точка пересечения его высот)
Гипотенуза прямоугольного треугольника лежит на прямой 2x + y – 2 = 0, а точка С(3; -1) является вершиной прямого угла. Площадь треугольника равна 9/4. Составить уравнения прямых, на которых лежат катеты
Основание равнобедренного треугольника лежит на прямой x + 2y – 2 = 0, а одна из боковых сторон – на прямой y + 2x – 1 =0. Составить уравнение другой боковой стороны треугольника, зная, что ее расстояние от точки пересечения данных прямых равно 
Составить уравнения сторон квадрата, в котором одна из вершин – точка (8;7) и одна из сторон лежит на прямой 5x + 2y + 4 = 0
Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 2x + y – 8 = 0, концы которого лежат на окружности (х – 3)2 + y2 = 4
Точки М(3;7) и N(2;3) являются серединами оснований равнобедренной трапеции. Точки К(1;7) и Р(4;6,5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции
Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать
Даны стороны треугольника: (АВ) 4x + 3y – 10 = 0; (ВС) 3x + 2y – 8 = 0; (АС) 8x + 5y – 18 = 0. Составить уравнение прямой, проходящей через точку С и делящей сторону АВ в отношении 2:3 (считая от вершины А)
Противоположными вершинами квадрата являются точки
(-5;-3) и (3;17). Найти координаты двух других вершин
Написать уравнения сторон треугольника, зная одну его вершину (2;7), уравнения медианы 9x + y + 4 = 0 и высоты x + 5y – 11 = 0, проведенных из различных вершин
Написать уравнения сторон треугольника, зная одну его вершину (-5;4), уравнения высоты 6x + y – 61 = 0 и биссектрисы 4x – 3y + 7 = 0
Точка М(6;4) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой 3x – y + 2 = 0. Найти уравнения остальных сторон треугольника
Длина стороны ромба с тупым углом 120є равна 
. Меньшая диагональ параллельна биссектрисе 2 и 4 координатных углов. Диагонали пересекаются в точке (-4;6). Составьте уравнения сторон ромба
Точка Р(8;1) является серединой одного из оснований прямоугольной трапеции, а точка N(2;3) – серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x + 3y + 1 = 0. Составить уравнения сторон
Составьте уравнения трех сторон треугольника, в котором медиана 3x + 2y – 6 = 0 и биссектриса x – y = 0 проведены не из вершины (4;0), а из двух других вершин
Даны стороны треугольника: 4x – 3y + 26 = 0(АВ); x + 2y + 1 = 0(АС); 7x + 3y – 37 = 0(ВС). Найти точку пересечения медианы, проведенной из вершины В и высоты, проходящей через вершину С
Найти радиус и координаты центра окружности, проходящей через точку А(-1;8) и касающейся прямых х + 10 = 0 и 4x – 3y + 10 = 0
Видео:✓ Квадрат вписан в прямоугольный треугольник | Ботай со мной #129 | Борис ТрушинСкачать
Точка отстоит на одинаковых расстояниях от точек Р(7;8) и Q(1;2). Найти координаты точки К, если известно, что она лежит на прямой 4x – 5y + 27 = 0
📹 Видео
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
9 класс, 7 урок, Уравнение прямойСкачать
Уравнение прямой и треугольник. Задача про высотуСкачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Планиметрия 31-32 | mathus.ru | прямая проведена через середину стороны квадрата | площадьСкачать
Уравнение прямой на плоскости. Решение задачСкачать
Вся геометрия в одной задаче | Геометрия на плоскости | Аналитическая геометрия | КАК РЕШАТЬ?Скачать
Уравнения прямой на плоскости | Векторная алгебраСкачать
Вершины K и L квадрата KLMN с центром O лежат на стороне AB треугольника ABC.Скачать
Задача, которую боятсяСкачать
Задача о нахождении сторон треугольника, образованного отрезками, находящимися внутри квадратаСкачать
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать
