Стационарный режим нагрева уравнение теплового баланса и условие стационарности (8 видео)

Стационарный режим нагрева. Уравнение теплового баланса и условие стационарности

В общем тепловом балансе для каждого конечного интервала времени вследствие закона сохранения энергии имеет место уравнение теплового баланса

где Д 2 R. После подстановки этого выражения в формулу (4.6) получим уравнение, связывающее ток стационарного режима I и стационарное превышение температуры 0:

Если известна допустимая температура нагрева поверхности аппарата или соединительного проводника (кабеля, провода, шины) и температура окружающего пространства, то в принципе можно рассчитать длительно допустимый ток /дд, зная геометрические параметры теплоотдающей поверхности и коэффициент теплопередачи.

Выбор соединительных проводников

Длительно допустимая температура аппаратов и соединительных проводников определяется классом использованной изоляции и в некоторых случаях допустимой температурой прикосновения человека, если к нагретой поверхности имеет доступ оператор. В типичных применениях температура окружающего пространства О₀ задана нормами МЭК. Поэтому может возникнуть нижеследующая задача.

Типовая задача 1

Исходные данные: медная шина поперечного сечения bx h = 5 х 60 мм 2 находится в спокойном воздухе. Коэффициент теплопередачи в окружающее пространство k_T = 12 Вт/(м 2 • К). Необходимо найти допустимый ток, если допустимая температура шины Ь_л — 65°С, а согласно МЭК 0„ — 35°С.

? Решение этой задачи основано на использовании соотношения (4.7). При решении следует учесть зависимость сопротивления от температуры. Поэтому сначала в таблицах справочных данных о свойствах материалов, чтобы использовать (4.2), найдем для меди удельное сопротивление при 0°С р₀ = 1,62 • К) 8 Ом • м и температурный коэффициент удельного сопротивления а = 4,3 • 1(Р 3 1/К. Площадь поперечного сечения шины составляет s = 5 х 60 мм 2 = 300 • 10 -6 м 2 , а периметр поперечного сечения П = 2(b + h) = 2(5 + 60) = 130 мм = 0,13 м. Записав соотношение (4.7) для некоторого участка шины произвольной длины /, получим уравнение относительно неизвестного допустимого тока:

Сокращая на величину / и подставляя уже известные значения, найдем

1. Длительно допускаемый ток присоединительных проводников должен быть не менее номинального рабочего тока защищающего аппарата — автоматического выключателя. Это требование обусловлено тем, что, во-первых, защитный аппарат должен защитить от перегрузки присоединительные проводники и, во-вторых, температура присоединительного проводника не должна быть выше, чем температура внутри аппарата. Э го второе условие должно соблюдаться с тем, чтобы присоединительные проводники не нагревали сам аппарат.
2. На практике при определении длительно допустимых токов можно и целесообразно пользоваться нормами стандартов [3] и Правил [4), которые учитывают многообразные способы прокладки проводников.

Типовая задача 2

Исходные данные: медная шина, рассмотренная в типовой задаче 1, используется в условиях, когда температура окружающего воздуха не превосходит Ь₀ = 25°С и допускается длительно температура 70°С. Как изменится длительно допускаемый ток при таком изменении окружающей и допускаемой температур?

? При решении этой задачи следует учесть как изменение допускаемого превышения температуры, которое станет равно 45°С, так и изменение длительной температуры, которая влияет на сопротивление проводника. При температуре 70°С удельное сопротивление меди станет равно р = 2,11 • 10 8 Ом • м. После подстановки полученных числовых значений получим длительно допустимый ток, равный 998 A. i

Типовая задача 3

Исходные данные: медная шипа, рассмотренная в типовой задаче 1, используется в условиях, когда допускается увеличение температуры окружающего воздуха до 50°С. Это реальное условие соблюдается, если рассмотрению подлежит присоединение шины к автоматическому выключателю, когда и выключатель, и шина расположены внутри шкафа низковольтного распределительного устройства. Как изменится длительно допускаемый ток?

? Для решения используем расчетное выражение, полученное в типовой задаче 1, с измененными значениями температур:

Как следует из решения последней задачи, рекомендации нормативных документов могут не соответствовать реальным условиям эксплуатации. На практике, при определении длительно допустимых токов проводников и аппаратов, размещаемых в низковольтных шкафах распределительных щитов, следует уч итывать рекомендации производителей аппаратов и щитов. В качестве примера можно ознакомиться с каталожными данными щитов Prisma, поставляемых компанией Schneider Electric.

Содержание

Тепловое равновесие и уравнение теплового баланса
Что такое теплообмен и при каких условиях он происходит
Уравнение теплового баланса и сохранение тепловой энергии
Уравнение теплового баланса
Если несколько тел участвуют в процессе теплообмена
Пример расчетов для теплообмена между холодным и горячим телом
Задача для самостоятельного решения:
Нагрев токоведущих частей и уравнение теплового баланса
📺 Видео

Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Тепловое равновесие и уравнение теплового баланса

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Видео:Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

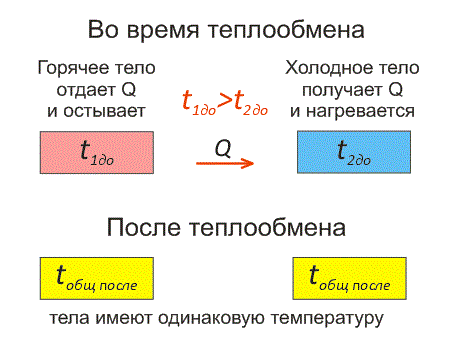
Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Видео:Решение задач на уравнение теплового баланса. Физика 8 классСкачать

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

(large Q_<text> left( text right) ) – это количество теплоты горячее тело теряет.

(large Q_<text> left( text right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_ + Q_ = 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

равными по модулю и
имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed < Q_+ Q_ + Q_ + ldots + Q_ = 0 > ]

Q для каждого нагреваемого тела будет обладать знаком «+»,
Q для каждого охлаждаемого тела — знаком «-».

Видео:Теплообмен. Уравнение теплового баланса 8-10 класс | Физика TutorOnlineСкачать

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

2). Теперь запишем формулу для каждого количества теплоты:

Примечания:

(large c_<text> ) – удельную теплоемкость воды находим в справочнике;
Массу воды переводим в килограммы;
Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_<text> — t_<text> ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_<text> — t_<text> ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_<text> — 80 ) + 4200 cdot 0,1 cdot (t_<text> — 15 ) = 0 ]

[large 840 cdot (t_<text> — 80 ) + 420 cdot (t_<text> — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

(large Q_ ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
(large Q_ ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
(large Q_ ) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Видео:Урок 127 (осн). Задачи на уравнение теплового баланса - 1Скачать

Нагрев токоведущих частей и уравнение теплового баланса

При работе токоведущих частей выделяют продолжительный и кратковременный режимы нагрева. Оборудование электростанций и подстанций в нормальных условиях работает в продолжительном режиме, а при коротких замыканиях в кратковременном режиме нагрева.

Процесс нагрева проводников в этих режимах можно описать с помощью уравнения теплового баланса. Составим это уравнение.

Пусть по длинному проводнику, имеющему сопротивление R, удельную теплоёмкость c, массу m и помещённому во внешнюю среду с температурой θ_ср протекает ток I. Для малого интервала времени dt можно составить уравнение теплового баланса:

. (1)

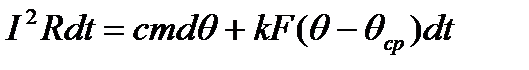
Здесь левая часть уравнения определяет тепло, которое выделилось в проводнике за время dt, первый член правой части определяет тепло расходованное на повышение температуры проводника на dθ градусов за время dt. Второй член правой части определяет тепло выделившееся в окружающую среду за время dt при условии, что k – коэффициент теплоотдачи, учитывающий все её виды (теплопроводность, конвекция, излучение), F – поверхность проводника, а θ – температура проводника.

Продолжительный режим нагрева – это режим с постоянной нагрузкой в течение неограниченного времени, когда проводник или аппарат находится в установившемся тепловом состоянии, достигая неизменной температуры.

Каждый проводник и изоляционный материал имеют допустимые температуры в продолжительном режиме θ_доп.дл. Например, изоляция в зависимости от класса имеет следующие допустимые температуры:

класс	У	А	Е	В	Р	Н	G
θ_доп.дл , 0 С	>180

Для неизолированных медных и алюминиевых проводников длительно допустимая температура 70 о С.

Уравнение теплового баланса в продолжительном режиме примет вид:

. (2), т.к. при некоторой установившейся температуре проводника θ_уст его температура не изменяется и, следовательно, dθ=0. На основании (2) можно получить связь между током в проводнике I в установившемся режиме и его температурой θ_уст:

.(3)

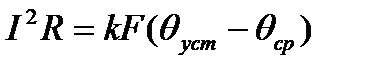
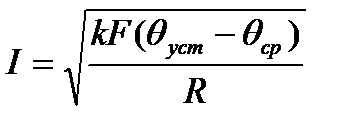
Номинальным называют длительно допустимый ток проводника, при котором проводник достигает длительно допустимой температуры θ_доп.дл при стандартизированной температуре окружающей среды θ_ср.ст.

Среда	_{СТАНДАРТИЗИРОВАННАЯ ТЕМПЕРАТУРА θср.ст}, о С
Воздух для проводников	+25
Воздух для аппаратов	+35
Земля	+15
Вода	+15

На основании (3) можно получить выражение для I_ном:

. (4)

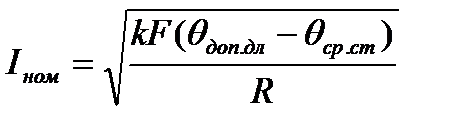
Если температура окружающей среды не равна стандартной, то говорят о допустимом токе проводника при данных условиях:

. (5)

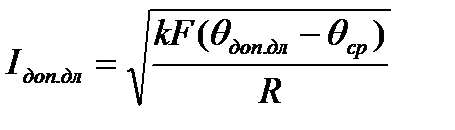
Если взять отношение допустимо длительного и номинального токов, то можно получить связь между этими токами:

. (6)

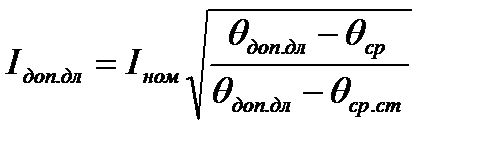
Из отношения произвольного тока в проводнике I и номинального тока можно определить установившуюся температуру проводника θ_уст при произвольной температуре среды θ_ср, отличной от стандартной:

. (7)

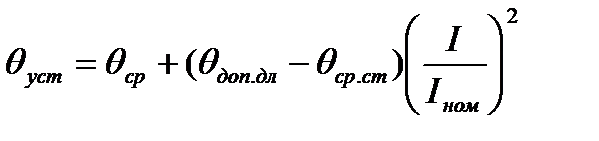
Нагрев проводников в кратковременном режиме. Критерием термической стойкости проводника в этом режиме является температура его нагрева токами КЗ. Проводники (и аппараты) считаются термически стойкими, если их конечная температура в процессе КЗ не превышает допустимой величины θ_{к доп}.

Определить конечную температуру нагрева проводника θ_к в процессе КЗ можно с помощью уравнения теплового баланса, которое из-за краткости режима КЗ, когда можно пренебречь выделением тепла в окружающую среду, примет вид:

. (8)

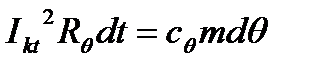
Здесь I_kt – ток КЗ (действующее значение), который с течением времени t может изменяться;

— активное сопротивление проводника при текущей температуре θ,

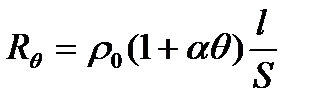
ρ₀ – удельное сопротивление проводника при θ=0 0 С;

l и S – длина и сечение проводника;

α – температурный коэффициент сопротивления;

— теплоёмкость проводника при температуре θ,

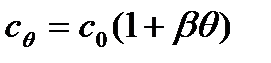
β – температурный коэффициент теплоёмкости;

m=γlS – масса проводника,

γ – плотность проводника.

Произведем подстановку в уравнение (8) рассмотренных выражений и проинтегрируем по соответствующим переменным:

. (9)

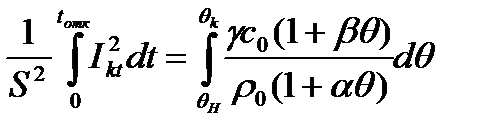
Здесь t_отк – время с начала КЗ до отключения,

θ_н – начальная температура проводника (перед КЗ),

θ_к – конечная температура проводника (в момент отключения КЗ).

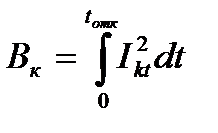
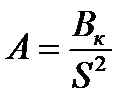
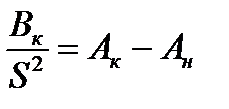
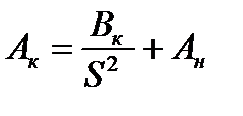
Величина пропорциональная количеству тепла, выделенного при КЗ, носит название теплового импульса, а величина носит название удельного теплового импульса. Значение интеграла в правой части соответствующее начальной температуре θ_н обозначим А_н, а конечной θ_k – А_к. Теперь можно записать:

или .

Величина А есть сложная функция температуры проводника и приводится в справочниках в виде графиков для проводников из различных материалов.

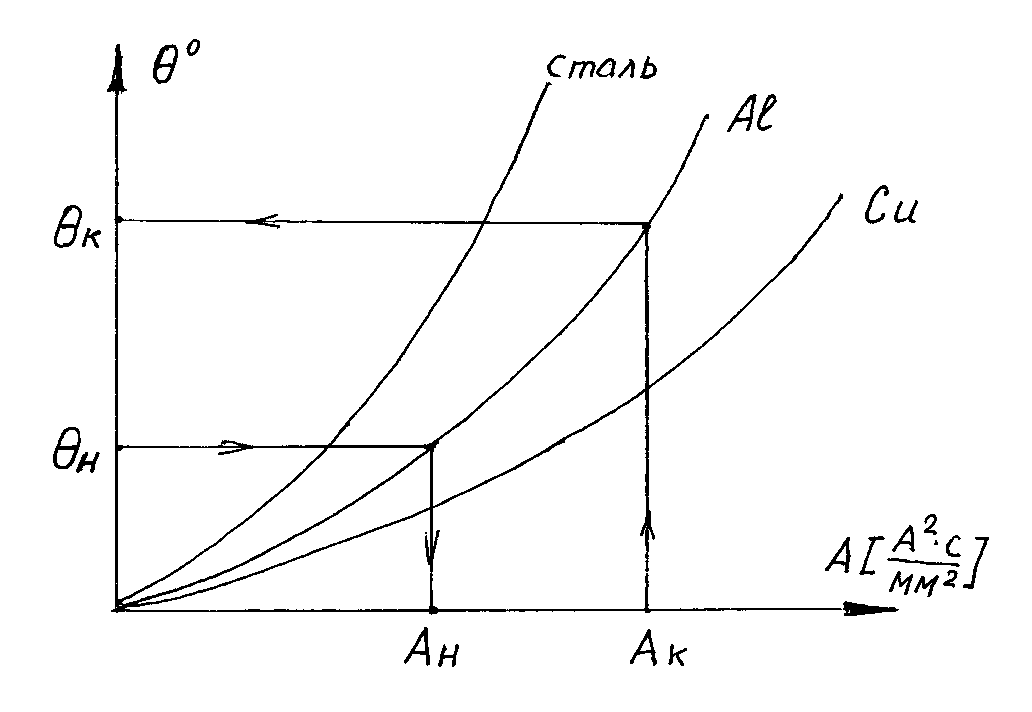
Рассмотрим, как с помощью этих графических зависимостей (Рис.9.1) определить конечную температуру проводника.

Рис. 9.1 Кривые для определения конечной температуры проводников.

В качестве начальной температуры θ_н принимаемустановившуюся температуру θ_уст проводника перед КЗ, которую вычисляем по ранее приведенной формуле (7), где I максимальный ток нагрузки в проводнике.

Зная θ_н, по кривой A=f(θ) определим А_н. Вычислив В_к, определим 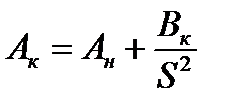, а затем по кривой определим конечную температуру θ_к.Если будет выполняться условие θ_к≤θ_{к доп}, то проводник в данных условиях будет термически стоек.

Таким образом, чтобы с помощью кривых A=f(θ) определить термическую стойкость проводников необходимо уметь вычислять тепловой импульс тока КЗ В_к. Так как ток КЗ в общем случае содержит периодическую и апериодическую составляющие, то и тепловой импульс В_к представляют состоящим из двух составляющих: В_кп – определяется переменной составляющей тока КЗ и В_ка – определяется апериодической составляющей тока КЗ. В_к≈В_{к п}+В_{к а}.

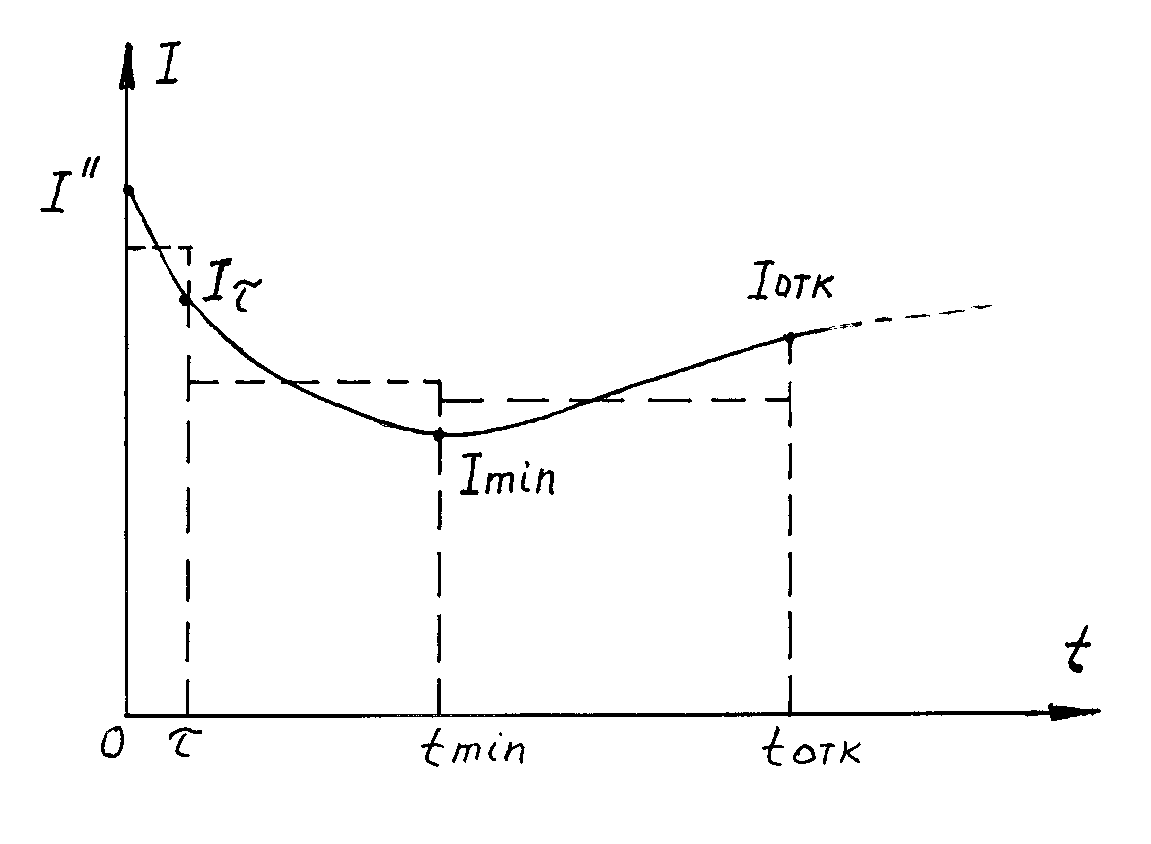
При КЗ недалеко от генераторов (КЗ на выводах генераторов, на сборных шинах распредустройств станций) действующее значение периодической составляющей тока КЗ из-за переходных процессов в генераторах и действия систем возбуждения генераторов изменяется во времени (Рис9.2). Это изменение необходимо учитывать при расчёте теплового импульса от периодической составляющей тока КЗ В_{к п}.

Рис. 9.2 Кривая изменения переменной составляющей тока КЗ для вычисления В_кп.

В расчете В_{к п} участвуют в общем случае следующие токи:

I ’’ – сверхпереходный ток КЗ;

I_τ – периодический ток КЗ в момент начала расхождения контактов выключателя;

I_min – минимальное значение периодического тока КЗ;

I_отк – периодический ток КЗ на момент отключения.

Время начала расхождения контактов выключателя τ=t_св+t_рз _min, здесь t_св – собственное время выключателя, а t_рз _min – минимальное время срабатывания основных защит в цепи выключателя (при отсутствии данных принимается 0,01 с).

Время отключения КЗ t_отк=t_во+t_рз _max, здесь t_во – время отключения выключателя t_рз _max – максимальное время срабатывания резервных защит в цепи выключателя.

Расчет В_кп основан на аппроксимации площади под кривой I 2 (t) прямоугольниками. При этом рассматриваются два случая:

;

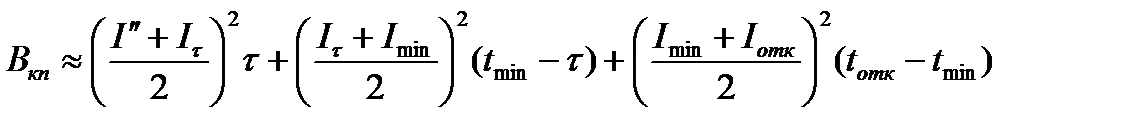
Апериодическая составляющая тока КЗ, возникнув в первый момент КЗ, затухает по экспоненциальному закону с постоянной времени петли КЗ Т_а. Можно показать, что при t_отк>Т_а тепловой импульс от апериодической составляющей можно принять В_ка≈I ’’2 Т_а.

Проверка термической стойкости аппаратов производится не по допустимой температуре, а по допустимому тепловому импульсу. Для этого в справочниках приводится ток термической стойкости I_тер и время его протекания t_тер. По ним можно вычислить допустимый тепловой импульс B_кдоп=I 2 _тер t_тер. Условием термической стойкости аппарата будет выполнение соотношения В_к≤В_{к доп}.

Аппараты и токоведущие части в цепях генераторов из-за длительного процесса гашения поля генератора при его отключении проверяют при условии, что t_отк=4с.

\|	следующая лекция ==>
Основные свойства связующих	\|	Мұғалімнің кәсіби өзін-өзі тәрбиелеуі

Дата добавления: 2016-02-09 ; просмотров: 5566 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ