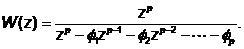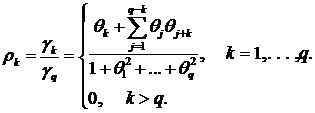Стационарный процесс авторегрессии ar 1 описывается уравнением (3 видео)

Содержание

Модели стационарных и нестационарных временных рядов и их идентификация
§ 5. Процесс авторегрессии AR(p)
Основные теоретические сведения
📺 Видео

Видео:Процесс авторегрессииСкачать

Модели стационарных и нестационарных временных рядов и их идентификация

Достаточно часто экономические показатели, представленные в виде временного ряда, имеют сложную структуру. Моделирование таких рядов путем построения модели тренда, сезонности и периодической составляющей не приводит к удовлетворительным результатам. Ряд остатков часто имеет статистические закономерности. Наиболее распространенными моделями стационарных рядов являются модели авторегрессии и модели скользящего среднего.

Будем рассматривать класс стационарных временных рядов. Задача состоит в построении модели остатков временного ряда u_t и прогнозирования его значений.

Авторегрессионная модель предназначена для описания стационарных временных рядов. Стационарный процесс удовлетворяет уравнению авторегрессии бесконечного порядка с достаточно быстро убывающими коэффициентами. В частности поэтому авторегрессионная модель достаточно высокого порядка может хорошо аппроксимировать почти любой стационарный процесс. В связи с этим модель авторегрессии часто применяется для моделирования остатков в той или иной параметрической модели, например регрессионной модели или модели тренда.

Модель авторегрессии порядка 1 AR(1) (марковский процесс).

Марковскими называются процессы, в которых состояние объекта в каждый следующий момент времени определяется только состоянием в настоящий момент и не зависит от того, каким путем объект достиг этого состояния. В терминах корреляционного анализа для временных рядов марковский процесс можно описать следующим образом: существует статистически значимая корреляционная связь исходного ряда с рядом, сдвинутым на один временной интервал, и отсутствует с рядами, сдвинутыми на два, три и т. д. временных интервала. В идеальном случае эти коэффициенты корреляции равны нулю.

Авторегрессионная модель первого порядка определяется соотношением:

где m — числовой коэффициент |m|

Модель (5.1) называется также марковским процессом.

Из (5.3) следует, что при |m| близком к единице дисперсия u(t) будет намного больше дисперсии e_t. Это значит (учитывая (5.2) m=r(u(t)u(t±1))=r(1), т.е. параметр m может быть интерпретирован как значение автокорреляции первого порядка), что в случае сильной корреляции соседних значений ряда u(t) ряд слабых возмущений e_t будет порождать размашистые колебания остатков u(t).

Условие стационарности ряда (5.1) определяется требованием |m| 2 (1))/(1-r 2 (1)). Для второго и выше порядков (см. [1], с. 413, 414) должно быть r_част(t)=0 «t=2,3,… . Это удобно использовать для подбора модели (5.1): если вычисленные по оцененным невязкам u(t)=y_t— выборочные частные корреляции статистически незначимо отличаются от нуля при t=2,3,…, то использование модели AR(1) для описания случайных остатков не противоречит исходным данным.

Идентификация модели. Требуется статистически оценить параметры m и s 2 модели (5.1) по имеющимся значениям исходного ряда y_t.

Выделяем неслучайную составляющую и получаем невязки . Находим дисперсию невязок , где (для большинства методов выделения автоматически =0). Далее с учетом (5.2), (5.3) получим формулы для оценки параметров модели (5.1):

Модели авторегрессии р порядка – AR(p) при p³2 см. в [1], с. 834-837:

Пример. График первой разности ряда, хорошо описывающейся моделью AR(1), представлен на рис. 5.1; график выборочной автокорреляционной функции (АКФ) первой разности этого ряда представлен на рис. 5.2. Ñ


Рис. 5.1	Рис. 5.2

Модели скользящего среднего порядка q (Moving Average — MA(q) models).

Часто на показатель в текущий момент времени оказывает воздействие значение показателя в предыдущие моменты. Хотя воздействие отдаленных элементов незначительно, в сумме оно может оказывать существенное влияние на модель. Учесть это воздействие возможно в модели скользящего среднего. Моделирование воздействия всех предшествующих элементов ряда на показатель в текущий момент основано на предпосылке о том, что в ошибках модели за несколько предшествующих периодов сосредоточена информация о всей предыстории ряда.

Моделью скользящего среднего порядка q называется процесс:

В частности, модели порядка 1 и 2 соответственно имеют вид:

Переход от формы (5.6) к форме (5.7) осуществляется с помощью последовательной подстановки в правую часть формулы (5.6) вместо u(t-1), u(t-2), … их выражений, вычисленных по формуле (5.6) для моментов времени t-1, t-2, …. Это означает двойственность в представлении анализируемого временного ряда – две эквивалентные формы линейного процесса — и обратимость AR и MA моделей.

В качестве примера рассмотрим модель скользящего среднего первого порядка – МА(1). Данная модель описывается соотношением (5.8). Можно показать, что стационарность u(t) обеспечивается при любом значении параметра q. Модель обратима (представима в виде модели авторегрессии бесконечного порядка) при условии |q| 2 модели (5.8) по имеющимся значениям исходного ряда y_t. Выделяем неслучайную составляющую и получаем невязки . Находим оценку автокорреляции :

Подставляя в выражение для автокорреляционной функции, имеем квадратное уравнение для q:

q 2 +(1/ )q+1=0.

Из двух решений приведенного квадратного уравнения (q₁q₂=1) одно будет меньше единицы – его и выбираем в качестве искомой оценки параметра в модели МА(1).

Оценка s 2 получается по формуле: .

Модель скользящего среднего второго порядка – МА(2) отличается более сложным построением -см. [1], с. 843-845.

Важное практическое значение имеют процессы, первая (или более высокая) разность которых стационарна и является процессом МА(q). Подобные процессы устроены как случайные колебания с непостоянным средним уровнем, или (для второй разности) непостоянным углом наклона.

Модели авторегрессии-скользящего среднего (AutoRegressive — Moving Average — ARMA(р, q) models).

На практике для экономичной параметризации анализируемого процесса иногда бывает необходимо включить в модель как члены, описывающие авторегрессию, так и члены, моделирующие остаток в виде скользящего среднего. Такой линейный процесс имеет вид:

и называется процессом авторегрессии — скользящего среднего порядка (p, q) – ARMA(p, q).

Рассмотрим в качестве примера модель ARMA(1,1). В соответствии с моделью (5.10) процесс ARMA(1, 1) описывается формулой:

Процесс ARMA(1, 1) стационарен, если корень характеристического уравнения AR(1) модели 1-mz=0 по модулю больше единицы. То есть должно быть |m| 2 модели по имеющимся значениям исходного ряда y_t.

Этап 1.

Этап 2. Из уравнения модели несложно получить систему уравнений вида:

Поделив первое уравнение системы на второе, получим квадратное уравнение относительно q:

A=-(1+q 2 )/q, где А=

Из двух корней уравнения выбираем тот, который удовлетворяет условию обратимости |q| 2 определяем из любого уравнения системы.

Модель авторегрессии — проинтегрированного скользящего среднего (AutoRegressive Integrated Moving Average — ARIMA(р, q, k) models).

Модель впервые была предложена Дж.Боксом и Г.Дженкинсом и поэтому известна как модель Бокса-Дженкинса. Это одна из наиболее популярных моделей для построения краткосрочных прогнозов значений временных рядов.

Будем рассматривать нестационарные, однородные временные ряды. То есть ряды, для которых случайный остаток u(t), получающийся после вычитания из ряда y(t) его неслучайной составляющей f(t), представляет нестационарный временной ряд. Модель Бокса-Дженкинса предназначена для описания нестационарных временных рядов со следующими свойствами:

а) в рамках аддитивной модели y(t) включает f(t), имеющий вид алгебраического полинома от t степени k-1, причем коэффициенты полинома могут быть как стохастические, так и нестохастические,

б) ряд y_k(t), t=1,2,…, n—k, получившийся из y(t) после применения к нему метода последовательных разностей, может быть описан моделью ARMA(р, q).

Следовательно, модель Бокса-Дженкинса имеет вид:

Введем операторы сдвига во времени:

Тогда оператор авторегрессии порядка p AR(p) имеет вид:

(F_—, m)=1-m₁F_——m₂F 2 _—— … —m_pF p _— ,

а оператор скользящего среднего порядка q MA(q):

(F_—, q)=1-q₁F_——q₂F 2 _—— … —q_qF q _— _.

Модель ARIMA(р, q, k) будет с учетом формулы (5.11) и введенных операторов иметь вид:

(F_—, m)D k y(t)= (F_—, q)e(t). (5.11 а )

На практике применяются модели ARIMA(р, q, k), в которых р, q, k не превышают 2. Например, ARIMA(1, 1, 1):

(F_—, m)Dy(t)= (F_—, q)e(t) Þ (1-mF_—)(y_t—y_t_-1)=(1-qF_—)e_t Þ

Частным случаем модели ARIMA является модель авторегрессии АR(p), для которой q=k=0. Другой частный случай — модель скользящего среднего MA(q), для которой p=k=0.

Важные специальные классы моделей — модели ARIMA(0, q, k), и модели ARMA(p, q) = ARIMA(р, q, 0).

Модель АR(1) при положительном коэффициенте автокорреляции представляет собой колебательный процесс с преобладанием длинных волн. Если коэффициент корреляции отрицателен, процесс является сильно осциллирующим. Модель ARIMA(0, 1, 1) описывает случайный процесс с непостоянным уровнем. Аналогичное утверждение справедливо для модели ARIMA(0, 2, 2), описывающей случайный процесс с переменным уровнем и углом наклона.

Идентификация ARIMA моделей.

Структура модели ARIMA описывается тремя параметрами (р, q, k). Кроме того, разные по форме модели могут быть довольно близки друг другу. Поэтому весьма важно по возможности правильно определить структуру модели. Рассмотрим этапы идентификации.

1. Подбирается порядок модели k. Для этого используется либо метод последовательных разностей, либо анализ автокорреляционных функций процессов Dy(t), D 2 y(t), … — пока не достигнем быстрого затухания (стационарности) автокорреляционной функции для некоторого k. Дж.Бокс и Г.Дженкинс предлагают взять за визуальный критерий стационарности быстрое убывание значений выборочной АКФ. Использование завышенного порядка разности приводит к росту дисперсии ошибок и к заметному росту дисперсии прогноза.

Пример. Для определения порядков авторегрессии и скользящего среднего продемонстрируем вид и свойства теоретических АКФ и частной АКФ простейших моделей.

Пример АКФ и частной АКФ для модели АR(1) представлен на рис. 5.3; 5.4. Пример АКФ и частной АКФ для модели АR(2) содержится на рис. 5.5; 5.6. Из содержания рис. 5.3-5.6 следует, что все значения частной АКФ для лагов, больших порядка авторегрессии, статистически незначимы. Пример АКФ и частной АКФ для модели MА(1) изображен на рис. 5.7; 5.8.


Рис. 5.3	Рис. 5.4

Рис. 5.5	Рис. 5.6

Рис. 5.7.	Рис. 5.8.

Пример АКФ и частной АКФ для модели MА(2) представлен на рис. 5.9; 5.10. Для модели MА(q) все значения АКФ для лагов, больших q, равны нулю. Для модели ARMA(р, q) значения АКФ после лага p-q представляют собой смесь затухающих синусоид и экспонент, а значения частной АКФ ведут себя аналогично после лага q-p. Ñ


Рис. 5.9	Рис. 5.10

Общий подход Бокса-Дженкинса к анализу временных рядов показан на рис. 5.11. Схема процесса выбора модели временного ряда показана на рис. 5.12.

Если процесс выбора модели успешно осуществлен, возникает проблема оценки качества построенной модели. Для «хорошей» модели остатки должны быть «белым шумом», т.е. их выборочные автокорреляции не должны значимо отклоняться от нуля. Кроме того, модель не должна содержать лишних параметров, т.е. нельзя уменьшить число параметров без появления значимой автокорреляции остатков. Для диагностики модели необходимо попытаться модифицировать ее, меняя порядки авторегрессии и скользящего среднего. Одновременно повышать оба порядка не рекомендуется ввиду опасности вырождения модели.

Видео:АвторегрессияСкачать

§ 5. Процесс авторегрессии AR(p)

Рассмотрим процесс y(t), значения которого в момент времени t формируются как комбинация значений этого процесса в предшествующий момент (t — 1) и некоторой случайной составляющей є,, независимой от значений y(t — 1).

Рис. 9.6. Процесс авторегрессии первого порядка AR(1)

Случайный процесс y(t) называется процессом авторегрессии первого порядка AR(1), если для него выполняется соотношение:

где ф — некоторая константа.

Из условия стационарности вытекает, что My(t) = 0. Доказано, что процесс AR(1) будет стационарным при |ф| lt; 1.

Дисперсия процесса равна Dy(t) = ® . Отсюда видно, что ес-

ли последовательные значения ряда сильно коррелированны (|ф| близко к 1), то дисперсия процесса будет значительно больше дисперсии случайного фактора. Следовательно, незначительные возмущения будут вызывать значительные колебания.

Автокорреляционная функция r(k) = фк, убывает по абсолютной величине с ростом лага по показательному закону.

Рис. 9.7. Теоретическая коррелограмма процесса AR(1), ф = 0,8

Для процесса AR(1) ( ф = 0,8) теоретический частный коэффициент автокорреляции первого порядка равен 0,8.

Рис. 9.8. Теоретическая коррелограмма процесса AR(1), ф = -0,8 Для процесса AR(1) ( ф = -0,8) теоретический частный коэффициент автокорреляции первого порядка равен -0,8. Коэффициенты более высоких порядков равны нулю.

Стационарный процесс авторегрессии первого порядка с ненулевым средним определяется соотношением:

Учитывая стационарность процесса, получим следующие формулы для оценки параметров:

Процесс авторегрессии первого порядка:

при ф gt; 1 является нестационарным взрывного типа, оценки его автокорреляционной функции растут с увеличением сдвига во времени.

При ф = 1 процесс AR(1) называется случайным блужданием, а взятие первой разности приведет к стационарному процессу (см. ниже процессы ARIMA).

Рис. 9.9. Процесс случайного блуждания y(t) = y(t _ 1) + st

Рассмотрим процесс AR(2). Случайный процесс y(t) называется процессом авторегрессии второго порядка, если выполняется соотношение:

где Ф1 ,ф2 — некоторые константы.

Из условия стационарности вытекает, что My(t) = 0.

Условие стационарности также накладывает ограничения на параметры ф1 ,ф2

Процесс авторегрессии второго порядка с ненулевым средним определ

Учитывая стационарность процесса, можно получить следующие формулы для оценки параметров:

Для процесса AR(2) теоретическая автокорреляционная функция плавно убывает по абсолютной величине. Теоретические частные коэффициенты автокорреляции первого и второго порядков отличны от нуля, коэффициенты более высоких порядков равны нулю.

Рассмотрим процесс AR(p). Случайный процесс y(t) со средним значением называется процессом авторегрессии порядка р, если выполняется соотношение:

Если среднее значение процесса равно нулю, тогда имеем:

В общем случае автокорреляционная функция стационарного AR-процесса является суммой затухающих экспонент и затухающих синусоидальных волн.

Для оценки параметров используют систему уравнений Юла- Уолкера, предварительно определив выборочные автокорреляционные функции:

Тогда система может быть записана в виде:

а ее решение будет иметь вид:

В общем случае условие стационарности процесса AR(p) формулируют в терминах корней его характеристического уравнения. Для стационарности процесса (9.17) необходимо и достаточно, чтобы все корни его характеристического уравнения

Для того чтобы выписать решение в явном виде, перейдем к матричным обозначениям:

лежали вне единичного круга, т. е. превосходили бы по модулю единицу. В общем случае корни уравнения (9.18) являются комплексными числами.

Видео:Что такое Стационарные и нестационарные временные ряды?Скачать

Основные теоретические сведения

ЛАБОРАТОРНАЯ РАБОТА 7

Моделирование параметрических временных рядов

Цель работы:ознакомить студентов с параметрическими временными рядами.

Основные теоретические сведения

1.1 Авторегрессионные (AutoRegression) модели порядка р — AR(p) — определяются следующим образом:

(1)

В выражении (1) величины ₁, . . . , _р используются для обозначения набора весовых коэффициентов; a_t определяет белый шум, т.е. a_t

В равенстве (1) переменная Х_t регрессирует на свои предшествующие значения, поэтому модель называется авторегрессионной. Следовательно, авторегрессионный процесс можно охарактеризовать как модель, в которой текущее значение ряда в момент t выражается через конечное число прошлых значений (систематическая зависимость от прошлых значений) и величину возмущения a_t, не зависящую от прошлого.

Для изучения свойств временного ряда (ВР) удобно ввести оператор сдвига назад, равный , т.е. действие этого оператора на ВР дает значение ряда в предыдущий момент времени. Последовательное применение оператора сдвига р раз определяет значение ВР в момент времени на р периодов ранее, что позволяет ввести степень сдвига оператора

С помощью оператора сдвига модель (1) можно записать в эквивалентной форме

которая после введения оператора авторегрессии принимает вид

Формально процесс AR(p) можно представить как прошедший через фильтр белый шум. Передаточная функция такого фильтра определяется как

Соответствующее характеристическое уравнение имеет вид

z p – ₁ z p -1 — ₂ z p -2 — …- _p = 0. (2)

В случае, если все р корней уравнения (2) находятся внутри окружности единичного радиуса (все корни по модулю меньше единицы), то процесс AR(p) является стационарным.

Автокорреляции удовлетворяют соотношению:

Из выражения (1) получаем для процесса AR(1) уравнение в виде

X_t = ₁ X_t _—₁ + a_t . (3)

Для автокорреляционной функции (АКФ) процесса AR(1) имеем

ρ_h = ₁ h для h > 0. (4)

1.2 Модель скользящего среднего (Moving Average) порядка q —MA(q) определяется как

(5)

где символы q₁, . . . , q_q используются для обозначения конечного набора весовых параметров.

Эта модель предполагает, что в ошибках модели в предшествующие периоды сосредоточена информация по всей предистории ряда.

Соотношение (5) определяет процессМА(q), который представляет собой линейную комбинацию текущего и прошлых значений шума a_t.

Используя оператор сдвига назад В, можно записать для процесса (5) эквивалентное выражение

(6)

Из равенства (6) следует, что процесс скользящего среднего можно трактовать как выход Х_t линейного фильтра с передаточной функцией q(B), на вход которого поступает белый шум a_t. Как видно из соотношения (5), процесс Х_t при любом n ≥ q определяется конечным числом значений a_t , а_t _{– 1} , . . . , а_t _– _q белого шума, поэтому такой фильтр принято называть фильтрами с конечной памятью. При n ≥ q процесс является стационарным со средним значением E <Х_t> = 0.

Для АКФ следует очевидное представление

Таким образом, для модели МА(q) автокорреляция обрывается на задержке q, и конечная протяженность автокорреляции является характерным свойством этой модели. В этой модели статистическая связь между наблюдениями сохраняется в течение q единиц времени (т.е. протяженность памяти процесса равна q).

Полученный результат принципиально различает процессы AR(р) и МА(q): если у процесса AR(р) при τ → ∞ (монотонно или колебательно) АКФ постепенно стремится к нулю, то у процесса МА(q) при τ = q АКФ обрывается и в последующем остается равной нулю.

Для модели МА(1) из (5) получаем

Для АКФ элементарные преобразования дают

Таким образом, для модели МА(1) при лаге, равном 1, АКФ не равна нулю, но для больших значений лагов АКФ обращается в нуль. М Можно сказать, что АКФ модели МА(1) обрывается на лаге, равном 1, т.е. модель МА(1) не «помнит», что произошло в момент, соответствующий двум временным интервалам назад!

1.3 Смешанные модели АRMA (р,q)

Моделями АR(р) и МА(q) за счет выбора их порядков р и q можно удовлетворительно описывать многие реальные процессы. Однако на практике такие процессы становятся чересчур громоздкими из-за необходимости применения моделей высокого порядка для адекватного описания динамической структуры данных. Для достижения большей гибкости в подгонке моделей к наблюдаемым ВР иногда бывает целесообразным объединить в одной модели и авторегрессию, и скользящее среднее. Решению этой задачи помогает рассмотрение смешанных моделей авторегрессии — скользящего среднего, т.е. моделей АRMA (р,q), которые имеют следующий вид

X_t = ₁ X_{t -1} + …+ _p X_{t -p} + a_t + θ₁ а_t _{– 1} +…+ θ_q а_t _– _q (9)

или в другой эквивалентной форме через операторы

(В) X_t = θ(В) a_t, (10)

где (B), q(B) — операторы, определенные ранее для моделей АR(р) и МА(q); — оператор сдвига назад.

Используя выражение (10), можно сделать следующие выводы:

· ВР <X_t> является AR-процессом порядка р, т.е. AR(р), если θ(В)= 1 или (В) X_t = e_t , где e_t подчиняется процессу скользящего среднего порядка q , т.е. e_t = θ(В) a_t;

· ВР <X_t> является МА-процессом порядка q, т.е. MA(q), если (В)= 1 или X_t = θ(В)b_t, где b_t подчиняется процессу авторегрессии порядка р, т.е. (В)b_t = a_t.

Таким образом, (В) X_t = θ(В) (В)b_t =θ(В) a_t.

Очевидно, что члены со скользящим средним в правой части (9) не оказывают влияния на условия стационарности процесса авторегрессии. Вследствие этого выражение (10) является стационарным процессом при условии, что все корни характеристического уравнения (В) = 0 лежат вне единичного круга.

В простейшем случае для модели АRMA (1,1) из (9) имеем

X_t = ₁ X_t _-1 + a_t + θ₁ а_t _{– 1}. (11)

Свойства модели АRMA(1,1) являются обобщением свойств модели АR(1) с некоторыми незначительными изменениями, вызванными воздействием компонента модели MA(1).

АКФ модели АRMA(1,1) с использованием предыдущих результатов определяется следующим образом

ρ₁ = ₁ + θ₁ σ_a 2 / γ₀, ρ_h = ₁ ρ_h _{– 1} для h > 1, (12)

где γ₀ — дисперсия процесса АRMA (1,1).

Таким образом, АКФ модели АRMA (1,1) ведет себя во многом подобно изменению АКФ модели АR(1) за исключением того, что экспоненциальный спад начинается с лага h = 2, следовательно, АКФ процесса АRMA (1,1) не обрывается на любом конечном лаге.

Идентификация порядка

Методы идентификации, по существу, представляют собой процедуры, которые применяются к данным наблюдений для выявления типа моделей с целью использования последних в дальнейших исследованиях, например, при прогнозировании. Цель идентификации заключается в том, чтобы получить некоторую информацию о конкретных значениях параметров p и q, определяющих вид модели.

Для определения порядка р модели авторегрессии можно использовать частную автокорреляционную функцию (ЧАКФ). ЧАКФ временного ряда является функцией его АКФ и служит полезным средством для определения порядка модели AR(p). Отметим, что АКФ определяется ковариацией между значениями процесса, отстоящими на τ шагов по времени друг от друга. Однако на поведение процесса AR(p) статистически влияет не только его значение в момент, равный τ шагов назад, но и все промежуточные значения процесса между моментами t и t – τ. ЧАКФ исключает влияние всех промежуточных значений ряда и показывает лишь «чистую» взаимосвязь между моментами t и t – τ.

Для модели AR(p) выборочная ЧАКФ обрывается на лаге р, что и может служить идентификацией порядка этой модели.

Модель скользящего среднего

Автокорреляционная функция является полезной при идентификации порядка рассматриваемой МА-модели. ВР X_t описывается моделью МА(q), если его АКФ ρ_q ≠ 0, но значение ρ_l = 0 при l > q.

В рассмотренных моделях AR(p) и MA(q) вид АКФ и ЧАКФ дает возможность идентифицировать параметры этих процессов. Напомним, что процесс <X_t> описывается моделью MA(q), если соответствующая АКФ срезается до нуля на лаге q. С другой стороны, ЧАКФ процесса <X_t> обрывается на лаге р при описании последнего моделью AR(p).

Процесс ARMA(p,q) объединяет свойства моделей AR(p) и MA(q), поэтому у процесса ARMA(p,q) при лагах τ > q действие его компонента в виде скользящего среднего прекращается и оказывает влияние только авторегрессионная составляющая. Вследствие этого при τ > q поведение АКФ процесса ARMA(p,q) аналогично характеру изменений АКФ процесса AR(p), т.е. с увеличением лага постепенно стремится к нулю.

С другой стороны, рассмотрение частных автокорреляций приводит к следующему: в связи с тем, что ЧАКФ процесса AR(p) становится равной нулю при лагах τ > р, то на поведение ЧАКФ процесса ARMA(p,q) при τ > р влияет его составляющая в виде MA(q). В итоге, это приводит к тому, что ЧАКФ процесса ARMA(p,q) постепенно сходится к нулю.

Было установлено, что АКФ такого процесса, содержащая компонент авторегрессии порядка р и составляющую скользящего среднего порядка q, после первых (q – р) задержек представляется в виде суммы экспонент и затухающих синусоид. С другой стороны, ЧАКФ этой модели приближенно описывается суммой экспонент и затухающих синусоид после (p – q). Однако для смешанной модели АКФ и ЧАКФ не дают достаточной информации с точки зрения нахождения параметров р и q. В частности, визуальный анализ графиков АКФ и ЧАКФ не позволяет однозначно определить параметры р и q модели ARMA(p,q).