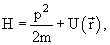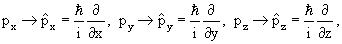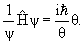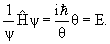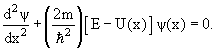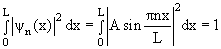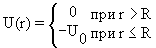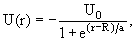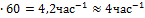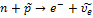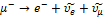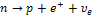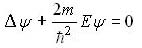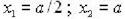Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- Уравнение Шредингера (общие свойства)
- Уравнение Шредингера (конкретные ситуации)
- СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- 📺 Видео
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
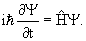 | (4.1) |
где 
в которой 







х → 


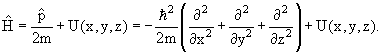 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


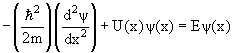
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
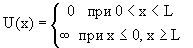 | (4.5) |
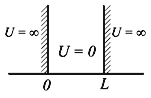
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
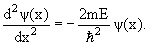 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
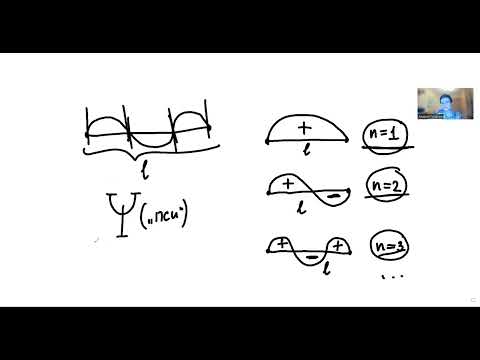
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
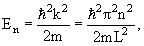 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
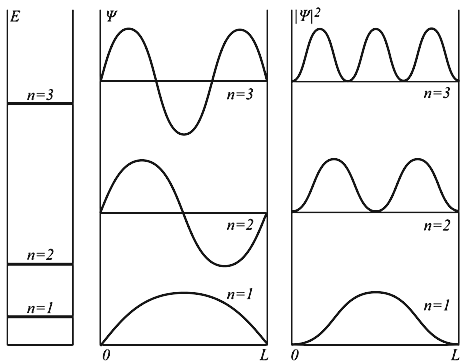
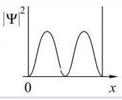
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
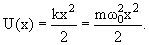 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
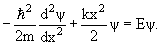 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
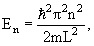

Одномерный гармонический осциллятор:
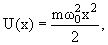
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
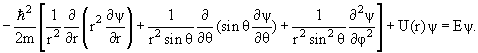 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
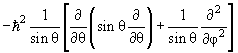 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 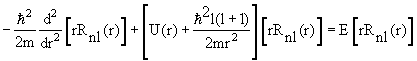 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
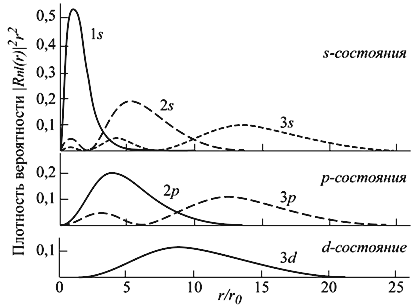
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
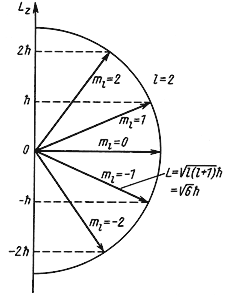
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
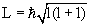 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
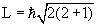
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Уравнение Шредингера (общие свойства)
№1 Стационарное уравнение Шредингера имеет вид 
Стационарное уравнение Шредингера в общем случае имеет вид




Линейного гармонического осциллятора
ü Частицы в одномерном потенциальном ящике с бесконечно высокими стенками
Частицы в трехмерном потенциальном ящике с бесконечно высокими стенками
Электрона в атоме водорода
Установите соответствия между квантовомеханическими задачами и уравнениями Шредингера для них.
Общий вид стационарного уравнения Шредингера имеет вид:


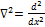
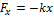

Значение потенциальной энергии электрона в потенциальном ящике с бесконечно высокими стенками U=0.Электрон в водородоподобном атоме обладаем потенциальной энергией 
Таким образом, для электрона в одномерном потенциальном ящике ур-ие Шредингера имеет вид:
С помощью волновой функции ,являющейся решением уравнения Шредингера ,можно определить….
Варианты ответа: (Укажите не менее двух вариантов ответа)
Средние значения физических величин ,характеризующих частицу
Вероятность того,что частица находится в определенной области пространства
Величина 
Уравнение Шредингера (конкретные ситуации)
№1Собственные функции электрона в одномерном потенциальном ящике с бесконечно высокими стенками имеют вид 

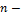

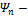


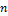
Число узлов 



Ядерные реакции.
№1В ядерной реакции 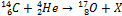
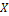
Из законов сохранения массового числа и зарядового числа следует, что заряд частицы равен нулю, а массовое число равно 1. Следовательно, буквой 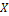
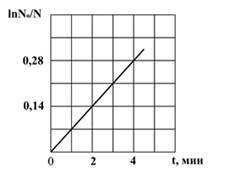
На графике в полулогарифмическом масштабе показана зависимость изменения числа радиоактивных ядер изотопа 
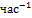
Число радиоактивных ядер изменяется со временем по закону 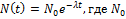
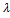
ln 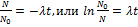

Законы сохранения в ядерных реакциях.
Реакция 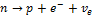
Во всех фундаментальных взаимодействиях выполняются законы сохранения: энергии, импульса, момента импульса (спина) и всех зарядов (электрического 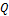
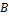
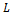
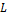
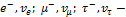
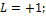

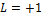
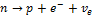
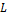
ü Лептонного заряда
Спинового момента импульса
Реакция 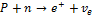
Во всех фундаментальных взаимодействиях выполняются законы сохранения: энергии,импульса,момента импульса(спина)и всех зарядов(электрического Q,барионного B и лептонного L).Эти законы сохранения не только ограничивают последствия различных взаимодействий,но определяют также все возможности этих последствий. Согласно закону сохранения барионного заряда B,для всех процессов с участием барионов и антибарионов суммарный барионный зарад сохраняется. Барионам (нуклонам n,p и гиперонам)приписывается барионный заряд
B=-1,а всем остальным частицам барионный заряд-B=0.Реакция 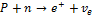
Варианты ответа: 
Законом сохранения электрического заряда запрещены реакции…
Варианты ответа(не менее 2):
При взаимодействии элементарных частиц и их превращении в другие возможны только такие процессы,в которых выполняются законы сохранения,в частности закон сохранения электрического заряда:суммарный электрический заряд частиц,вступающих в реакцию,равен суммарному электрическому заряду частиц,полученных в результате реакции.Электрический заряд Q в единицах элементарного заряда равен:у нейтрона (n) Q=0,протона (P) Q=+1, электрона ( 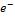
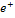
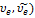
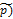


№1Известно четыре вида фундаментальных взаимодействий. В одном из них участниками являются все заряженные частицы, обладающие магнитным моментом, переносчиками –фотона. Этот вид взаимодействия характеризуется сравнительной интенсивностью 
Все перечисленные характеристики соответствуют электромагнитному взаимодействию. Его радиус действия равен бесконечности.
ü
Видео:Урок 455. Уравнение ШрёдингераСкачать

Уравнение Шредингера (конкретные ситуации)
Задание 1
Стационарным уравнением Шредингера для частицы в одномерном ящике с бесконечно высокими стенками является уравнение…
Варианты ответов:
1) 
2 
3) 
4)
Задание 2
Стационарным уравнением Шредингера для частицы в трёхмерном потенциальном ящике с бесконечно высокими стенками является уравнение …
Варианты ответов:
1) 
2) 
3) 
4)
Задание 3
Стационарное уравнение Шредингера в общем случае имеет вид: 
Варианты ответов:
1) 
3) 
Задание 4
Стационарным уравнением Шредингера для электрона в водородоподобном ионе является уравнение…
Варианты ответов:
1) 
2) 
3) 
4)
Задание 5
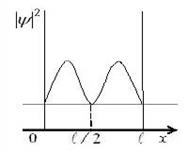
На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n=2 соответствует распределение…
Варианты ответов:
1) 


Задание 6
На рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность ее обнаружения в центре ямы равна…
Варианты ответов:
Задание 7
Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 

Варианты ответов:
Задание 8
Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 

Варианты ответов:
1) 5/8; 2) 3/8; 3) 1/2; 4) 1/4
Задание 9
Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 

Варианты ответов:
1) 3/8; 2) 1/2; 3) 5/8; 4) 1/4
Задание 10
Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле , 
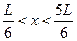
Варианты ответов:
Задание 11
Электрон находится в возбужденном состоянии (n=2) в одномерном потенциальном ящике шириной a c бесконечно высокими стенками. Плотность вероятности нахождения электрона максимальна в точках с координатами…
Варианты ответов:
1) 
2) 
3) 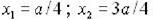
4)
Задание 12
Электрон находится в первой трети прямоугольного одномерного потенциального ящика с непроницаемыми стенками на втором энергетическом уровне. Вероятность найти электрон в центре этого потенциального ящика на этом же энергетическом уровне равна …
Варианты ответов:
Задание 13
Волновая функция частицы в потенциальной яме с бесконечно высокими стенками шириной L имеет вид: 
Варианты ответов:
1) 
2) 
Задание 14
Волновая функция частицы в потенциальной яме с бесконечно высокими стенками шириной L имеет вид: 

Варианты ответов:
Задание 15
Волновая функция частицы в потенциальной яме 

Варианты ответов
1) 


Задание 16
В потенциальной яме бесконечной глубины находится электрон. Волновые функции

д) нет верного ответа.
Задание 17
Электрон, имеющий кинетическую энергию 





 |
а) 
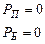

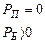
| Соответствующий случай | Буква |
Классическая теория,  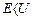 | |
Классическая теория,  | |
Квантовая теория, 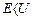 | |
Квантовая теория,  | |
| Неверный ответ |
Задание 18
Выберите правильный ответ для единиц измерения одномерной пси-функции (ψ=ψ(х))
б) 
в) 
г) 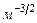
д) нет верного ответа
Задание 19
В потенциальной яме с вертикальными стенками находится электрон. Его волновая функция изображена на рисунке. В этом случае глубина потенциальной ямы
б) бесконечна слева, конечна справа;
в) бесконечна справа, конечна слева;
д) нет верного ответа.
Задание 20
Физический смысл пси-функции в том, что
а) её модуль описывает движение частицы;
б) она показывает плотность вероятности нахождения частицы в окрестности данной точки пространства;
в) квадрат её модуля показывает плотность вероятности нахождения частицы в окрестности данной точки пространства;
г) куб её модуля показывает вероятность нахождения частицы в данной точке пространства;
д) нет верного ответа.
Задание 21
Электрон находится в потенциальной яме с бесконечно высокими стенками. Для некоторых состояний в середине ямы пси-функция электрона может иметь узел, т.е. y=0. Выберите правильное высказывание:
а) пси-функция не может иметь узлов в яме с бесконечными стенками;
б) пси-функция не может иметь узел в центре ямы;
в) номера состояний кратны двум;
г) номера состояний кратны трем.
Задание 22
Частица находится в прямоугольной одномерной потенциальной яме с бесконечно высокими стенками в состоянии с главным квантовым числом n .Чему равно количество узлов пси-функции внутри ямы, не учитывая узлов (y=0) на границах ямы?
д) нет верного ответа.
Задание 23
Выберите правильное продолжение высказывания. Для макроскопических тел, например пылинки в спичечном коробке, мы не замечаем квантования уровней энергии, потому, что
а) макроскопические тела не подчиняются законам квантовой механики;
б) уровни энергии макроскопических тел расположены настолько редко, что квантование энергии не заметно;
в) уровни энергии макроскопических тел расположены настолько часто, что квантование энергии не заметно;
г) эксперименты по обнаружению квантования энергии макроскопических тел не проводились.
Задание 24
В потенциальной яме бесконечной глубины находится электрон. Волновые функции схематически представлены на рисунке. Ширину ямы уменьшили в два раза. Во сколько раз изменится при этом минимальное значение кинетической энергии электрона?
 |
Задание 25
Частица находится в одномерной бесконечно глубокой потенциальной яме прямоугольной формы. Установите соответствие между графиком зависимости 

 |
| Номер состояния | Соответствующая буква |
Задание 26
Условие нормировки пси-функции для частицы, находящейся в потенциальной яме с непроницаемыми стенками шириной l, заключается в том, что вероятность нахождения частицы внутри ямы равна:
г) 
д) нет верного ответа.
Задание 27
Выберите неверные утверждения
а) уравнение Шредингера описывает движение квантовой частицы;
б) уравнение Шредингера может быть получено уточнением законов Ньютона в классической механике;
в) квантовая теория настаивает на отказе от абсолютной определенности в задании начальных условий движения частицы;
г) в квантовой теории физический смысл имеет только вещественная часть комплексной волновой функции;
д) для макроскопических частиц предсказания квантовой и классической теории совпадают.
Задание 28
Частица находится в одномерной потенциальной яме прямоугольной формы с непроницаемыми стенками. Общее решение для стационарного уравнения Шрёдингера имеет вид:
а) 
б) 
в) 
г) 
д) правильных решений не приведено.
Задание 29
На рисунках схематично изображены зависимости от координаты плотности вероятности обнаружения частицы. Установите соответствие между формой одномерной прямоугольной потенциальной ямы и рисунком и заполните таблицу.
 |
| Форма потенциальной ямы | Соответствующая буква |
| Стенки ямы конечной высоты | |
| Обе стенки конечной высоты, правая стенка выше | |
| Обе стенки конечной высоты, левая стенка выше | |
| Левая стенка конечной высоты, правая – бесконечной | |
| Правая стенка конечной высоты, левая – бесконечной | |
| Стенки ямы бесконечной высоты |
Задание 30
Частица массы m находится в одномерной прямоугольной яме ширины l с непроницаемыми стенками в состоянии с пси-функцией Yn(x,t) и спектром энергии 
Видео:97. Микрочастица в потенциальной ямеСкачать

СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
ОПИСАНИЕ ПОВЕДЕНИЯ ЭЛЕКТРОНА В КВАНТОВОЙ МЕХАНИКЕ
1. Уравнение Шредингера
Для выполнения лабораторных работ 6 и 7 необходимо знакомство с основами квантовой механики. Остановимся на тех её положениях, которые непосредственно связаны с содержанием данных работ.
В них изучается поведение микрочастицы (электрона) в определенных внешних условиях. Это означает, что потенциальная энергия электрона U, Обусловленная его взаимодействием с окружающими объектами, является известной функцией координат: 




Называемое Временны́м уравнением Шредингера, где I – мнимая единица, ( H – постоянная Планка), Ñ2 – оператор Лапласа (имеющий в декартовых координатах вид 


2. Уравнение Шредингера для стационарных состояний
Среди решений уравнения (Б.1) особый интерес представляют волновые функции вида

Описывающие состояния, называемые Стационарными. Легко проверить, что волновая функция вида (2) будет решением уравнения Шредингера (1), если 

Где 



Уравнение (3) называется Уравнением Шредингера для стационарных Состояний, или Стационарным уравнением Шредингера. Существенно, что стационарное уравнение Шредингера имеет физически приемлемые решения, вообще говоря, не для любых значений Е, А лишь для некоторого множества 


3. Волновая функция и заключенная в ней информация
Как уже говорилось, волновая функция описывает состояние частицы. Это означает, что в 

(звездочка обозначает комплексное сопряжение). Важную информацию о движении частицы дает выражающийся через 

Называемый вектором плотности потока вероятности. Он указывает направление наиболее быстрого перемещения вероятности и дает скорость этого перемещения. Смысл величин (4) и (5) раскрывается в эксперименте, когда производится N Измерений над электроном в одном и том же состоянии. Тогда при больших значениях N должно выполняться: DN¢ / N

J , где DN¢ – число электронов, обнаруженных в единичном объеме вблизи точки (Х, у, z), а DN¢¢ – результирующее число электронов, прошедших за единицу времени в направлении вектора 
В связи с приведенной интерпретацией выражений (4) и (5) волновую функцию 
Отметим, что для стационарных состояний выражения (4) и (5) не зависят от времени и что для вещественных 

4. Оптическая аналогия
Анализируя квантовомеханическую задачу, полезно сопоставлять ее, с одной стороны, с аналогичной задачей классической механики, а с другой – с некоторой оптической задачей. В классической механике аналогом, очевидно, будет задача о частице такой же массы, движущейся в силовом поле, характеризуемом той же потенциальной энергией , что и в исходной квантовой. Выяснив характер движения классической частицы, можно лучше понять особенности ее квантовомеханического поведения. Оптическим аналогом для квантовомеханической задачи с
E = Const будет, Как можно показать, задача о распространении монохроматической световой волны в неоднородной среде, для которой показатель преломления N Изменяется по закону

Отметим, что длину волны при этом можно оценивать по соотношению де Бройля 

Аналогия с оптикой позволяет во многих случаях, не решая уравнение Шредингера, предвидеть и объяснить качественно поведение y-функции, а следовательно и частицы.
5. Одномерные квантовомеханические задачи
Среди квантовомеханических задач выделяются своей простотой одномерные, т. е. такие, в которых U = U ( X ), а волновую функцию 

А стационарное уравнение Шредингера сводится к уравнению в обыкновенных производных

Уравнение (8) решается особенно просто, когда ось X можно разбить на области, в каждой из которых потенциал U(X) принимает постоянные значения, а на границах соседних областей испытывает скачок. Такой потенциал называется Прямоугольным Из-за прямых углов на его графике. Строго говоря, такие потенциалы не реализуемы, поскольку им соответствуют бесконечные силы в точках скачков потенциальной энергии. Все же прямоугольные потенциалы дают грубое представление о многих реальных системах, позволяя получать полезные результаты крайне простыми математическими методами.
В области, где потенциал U Постоянен, при E > U стационарное уравнение Шредингера (8) сводится к уравнению
Где 

Где А И В – произвольные постоянные.
При этом, в соответствии с (9) и (7), зависящая от времени
Волновая функция 

В котором первое слагаемое описывает волну, бегущую вправо, а второе – влево. При переходе от одной области к другой U изменяется и, следовательно, изменяется длина волны. Существенно, что на границе между областями, как уже отмечалось, y(Х) и ее первая производная D Y / D x должны быть непрерывны. Это приводит к двум уравнениям связи между амплитудными коэффициентами А и В для соседних областей.
6. Движение электрона в области потенциальной ступеньки
Рассмотрим случай, когда потенциал испытывает только один скачок (Потенциальная Ступенька, рис. 1). Предположим, что электроны с некоторой энергией Е Приходят слева. Согласно классической механике электроны должны беспрепятственно проходить точку Х = 0, поскольку в этой точке они испытывает действие силы, направленной в сторону своего движения (ускоряющей силы).
Используем, прежде всего, оптическую аналогию. Согласно (6) при X= 0 происходит скачкообразное изменение показателя преломления N , а при падении света на поверхность раздела двух сред с различными N часть волны отражается от неё, а часть проходит во вторую среду. Поэтому следует ожидать отражения в точке Х = 0 и для y-волны, а следовательно, отличной от нуля вероятности отражения электрона при падении на скачок потенциала как справа, так и слева.
Подтвердим эти предположения строгим расчетом на основе стационарного уравнения Шредингера (8). В области I, слева от скачка потенциала (т. е. при Х 0) для случая, когда электроны падают только слева, решение содержит лишь одно слагаемое, соответствующее прошедшей волне

Где 







Поскольку K2 > K1 , амплитуды отраженной и падающей волн имеют противоположные знаки. Это означает, что для падающей слева волны её фаза при отражении от скачка потенциала изменяется на π – происходит «потеря» полуволны.
Плотность потока электронов Г может быть выражена через их концентрацию Пе И скорость v : Г = Ne V. Поскольку Пе

K|ψ|2. Доля электронов, которые проходят вправо, т. е. коэффициент прохождения DЕ,, равен отношению плотности прошедшего потока к плотности падающего:

Аналогично рассчитывается и коэффициент отражения:

Те же выражения получаются в результате подсчета коэффициентов 



Вытекающим непосредственно из определения вектора плотности потока вероятности 
Легко проверить также, что 

Следует подчеркнуть, что свойство отражения частиц от скачков потенциала является чисто квантовомеханическим эффектом. Оно вытекает из волновых свойств материи и не имеет места в классической физике.
В заключение сформулируем квантовомеханическую задачу, позволяющую на примере одномерной прямоугольной симметричной потенциальной ямы (рис. 2) простыми методами рассмотреть квантование энергии электрона и дать качественное объяснение эффекта Рамзауэра.
В этой задаче потенциальная энергия электрона U (Х) задается в виде:


Величина L = 2 а – Ширина ямы, 
В зависимости от полной энергии электрона E, Возникают три случая:
📺 Видео
Частица в одномерной потенциальной ямеСкачать

Классические уравнения | трёхмерное стационарное уравнение ШрёдингераСкачать

Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать

Урок 32. Уравнение ШрёдингераСкачать
Урок 456. Движение микрообъекта в одномерной бесконечно глубокой потенциальной ямеСкачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 1Скачать

Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 2Скачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Квантовая физика Л3. Волновая функция. Уравнение Шредингера. Потенциальный ящикСкачать

Атомная и ядерная физика. Лекция 6.2. Стационарное уравнение Шрёдингера. Частица в потенциальной ямеСкачать

Лекция 5: Стационарное уравнение ШредингераСкачать

Движение частицы в потенциальной яме.Скачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Урок 454. Понятие о волновой функцииСкачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Семинар 7. Стационарное уравнение Шредингера. Состояния дискретного спектра. Потенциальные ямы.Скачать