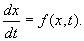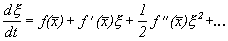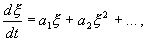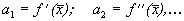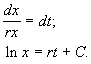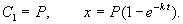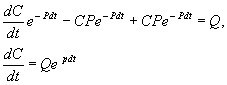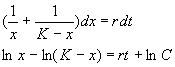МОДЕЛИ БИОЛОГИЧЕСКИХ СИСТЕМ, ОПИСЫВАЕМЫЕ
ОДНИМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ ПЕРВОГО ПОРЯДКА
Модели, приводящие к одному дифференциальному уравнению. Понятие решения одного автономного дифференциального уравнения. Стационарное состояние (состояние равновесия). Устойчивость состояния равновесия. Методы оценки устойчивости. Решение линейного дифференциального уравнения Примеры: экспоненциальный рост, логистический рост.
Изучение математических моделей биологических систем начнем с систем первого порядка, которым соответствует одно дифференциальное уравнение первого порядка:
Если система автономная, то правая часть уравнений не зависит явно от времени и уравнение имеет вид:
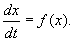
Состояние таких систем в каждый момент времени характеризуется одной единственной величиной – значением переменной x в данный момент времени t.
Рассмотрим плоскость t, x. Решениями уравнения (2.1): x( t) являются кривые на плоскости t, x , называемые интегральными кривыми (рис. 2.1)
Пусть заданы начальные условия 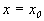
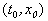
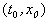
Рис. 2.1. Интегральные кривые x ( t ); – решения уравнения f ( x ) = 0

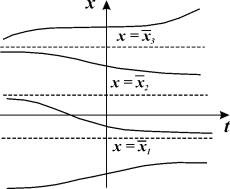
Интегральные кривые уравнения (2.1) не могут пересекаться. Решения уравнения (2.1) не могут быть периодическими, они монотонны.
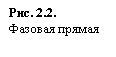
Поведение интегральных кривых на плоскости t, x можно установить, не решая в явном виде дифференциального уравнения (2.1), если известен характер движения изображающей точки на фазовой прямой.
Рассмотрим плоскость t, x , причем фазовую прямую совместим с осью x . Построим на плоскости t, x точку с абсциссой t и с ординатой, равной смещению изображающей точки по оси x в данный момент времени t. С течением времени в соответствии с уравнением (2.1) изображающая точка будет двигаться по фазовой прямой (рис. 2.2), а на плоскости t, x описывать некую кривую. Это будет интегральная кривая уравнения (2.1).
Решения одного автономного дифференциального уравнения либо уходят в бесконечность (чего не бывает в реальных системах), либо асимптотически приближаются к стационарному состоянию.
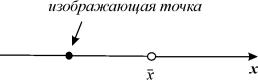
Стационарное состояние (точка покоя, особая точка, состояние равновесия)
В стационарном состоянии значения переменных в системе не меняются со временем. На языке дифференциальных уравнений это означает:
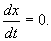
Если левая часть уравнения равна нулю, значит равна нулю и его правая часть:
Корни алгебраического уравнения (2.3): 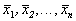
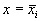
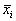
Реальные биологические системы испытывают многочисленные флуктуации, переменные при малых отклонениях возвращаются к своим стационарным значениям. Поэтому при построении модели важно знать, устойчивы ли стационарные состояния модели.
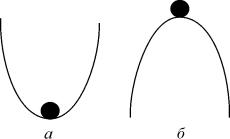
Рис. 2.3. К понятию устойчивости состояния равновесия

Устойчивость состояния равновесия
Каждый имеет интуитивное представление об устойчивости. На рис. 2.3. в обоих положениях (а и б) шарик находится в равновесии, т.к. сумма сил, действующих на него, равна нулю.
Попытайтесь ответить на вопрос : «Какое из этих состояний равновесия устойчиво?»
Скорее всего, Вы дали правильный ответ. Сказать, как Вы догадались? Вы дали шарику малое отклонение от состояния равновесия . В случае ( а) шарик вернулся. В случае ( б) покинул состояние равновесия навсегда.
Устойчивое состояние равновесия можно определить так: если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от особой точки, то особая точка будет устойчивым состоянием равновесия, что соответствует устойчивому режиму функционирования системы.
Строгое математическое определение устойчивости состояния равновесия уравнения dx/dt = f( x) выглядит следующим образом :
Состояние равновесия устойчиво по Ляпунову, если задав сколь угодно малое положительное 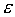
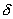
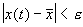
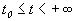
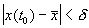
Иначе говоря, для устойчивого состояния равновесия справедливо утверждение: если в момент времени 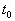
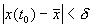
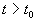
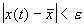
Другими словами: c тационарное состояние называется устойчивым, если малые отклонения не выводят систему слишком далеко из окрестности этого стационарного состояния. Пример — шарик в ямке (с трением или без трения).
Стационарное состояние называется асимптотически устойчивым, если малые отклонения от него со временем затухают. Пример — шарик в ямке в вязкой среде.
Стационарное состояние называется неустойчивым, если малые отклонения со временем увеличиваются. Пример: шарик на горке.
Устойчивое стационарное состояние представляет собой простейший тип аттрактора.
Аттрактором называется множество, к которому стремится изображающая точка системы с течением времени (притягивающее множество).
В нашем курсе мы рассмотрим следующие типы аттракторов:
· устойчивая точка покоя;
· предельный цикл — режим колебаний с постоянными периодом и амплитудой (начиная с размерности системы 2 );
· Области с квазистохастическим поведением траекторий в области аттрактора, например, «странный аттрактор» (начиная с размерности 3 ).
Аналитический метод исследования устойчивости стационарного состояния (метод Ляпунова). Линеаризация системы в окрестности стационарного состояния.
Метод Ляпунова приложим к широкому классу систем различной размерности, точечным системам, которые описываются обыкновенными дифференциальными уравнениями, и распределенным системам, описываемым уравнениями в частных производных, непрерывным и дискретным.
Рассмотрим метод линеаризации Ляпунова для одного автономного дифференциального уравнения первого порядка. Пусть 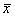
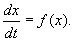
Пусть система, первоначально находившаяся в стационарном состоянии, отклонилась от него и перешла в близкую точку с координатой: 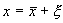

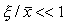
Перейдем в уравнении (2.1) от переменной x к переменной 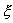
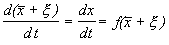
Учтем, что 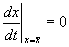
Правую часть разложим в ряд Тейлора в точке 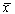
где
Отбросим члены порядка 2 и выше. Останется линейное уравнение:
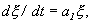
которое носит название линеаризованного уравнения или уравнения первого приближения. Интеграл этого уравнения для 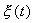
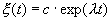
где 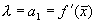
Если SYMBOL 108 f «Symbol» s 12 l SYMBOL 60 f «Symbol» s 12 0 , то при 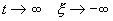
Если же SYMBOL 108 f «Symbol» s 12 l SYMBOL 62 f «Symbol» s 12 > 0 , то при 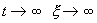
Если SYMBOL 108 f «Symbol» s 12 l =0 , то уравнение первого приближения не может дать ответа на вопрос об устойчивости состояния равновесия системы. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора. Такие случаи мы рассмотрим в лекции 6.
Аналогичные рассуждения проводятся при рассмотрении устойчивости стационарных состояний более сложных динамических систем.
Итак, устойчивость стационарного состояния 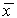
Видео:Устойчивость 1 ОпределениеСкачать

В случае одного уравнения вопрос об устойчивости состояния равновесия нетрудно решить, рассматривая график функции f(x).
По определению в стационарной точке правая часть уравнения (2.1) ‑ функция f(x) обращается в нуль.
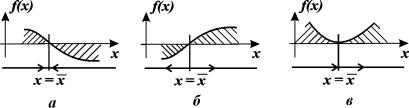
Здесь возможны три случая (рис. 2.4 а, б, в).
1. Вблизи состояния равновесия функция f(x) меняет знак с плюса на минус при возрастании x (рис. 2.4 а).
Отклоним изображающую точку системы в сторону 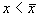
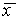
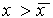
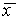
Рис. 2.4. Определение устойчивости стационарного состояния по графику функции f( x)
a – стационарное состояние 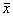
б, в ‑ стационарное состояние 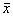
2. Вблизи состояния равновесия функция f ( x) меняет знак с минуса на плюс при возрастании x ( рис. 2.4 б) .
Проведите рассуждения, аналогичные случаю 1. Поместите изображающую точку в область 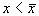
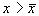
В обоих случаях изображающая точка удаляется от состояния равновесия. Стационарное состояние неустойчиво.
3. Вблизи состояния равновесия функции f(x) не меняет знак ( рис 2.4 в) .
Поскольку 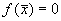
Вопрос. Является ли состояние равновесия в случае 3 устойчивым?
Ответ. Нет. По определению устойчивости.
1. Рост колонии микроорганизмов
За время D t прирост численности равен:
где R – число родившихся и S – число умерших за время SYMBOL 68 f «Symbol» s 12 D t особей пропорциональные этому промежутку времени:
В дискретной форме:
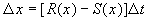
Разделив на SYMBOL 68 f «Symbol» s 12 D t и переходя к пределу при t SYMBOL 174 f «Symbol» s 12 ® 0 , получим дифференциальное уравнение
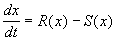
В простейшем случае, когда рождаемость и смертность пропорциональны численности:
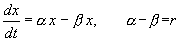
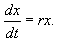
Разделим переменные и проинтегрируем:
Переходя от логарифмов к значениям переменной x и определяя произвольную постоянную С из начальных условий, получим экспоненциальную форму динамики роста.
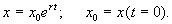
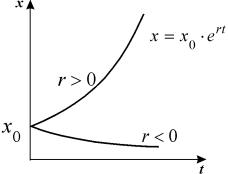
График функции (2.8) при положительных (размножение) и отрицательных (вымирание) значениях константы скорости роста представлен на рис. 2.5. Роль этой модели в развитии математической биологии и экологии мы обсудим в Лекции 3.
Рис. 2.5. Экспоненциальная форма динамики роста численности колонии микроорганизмов в соответствии с системой уравнений (2.7)

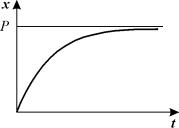
2. Вещество переходит в раствор
Пусть количество вещества, переходящего в раствор, пропорционально интервалу времени и разности между максимально возможной концентрацией Р и концентрацией x в данный момент времени: 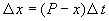
В форме дифференциального уравнения этот закон выглядит в
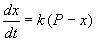
Разделим в этом уравнении переменные, и проинтегрируем:
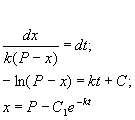
Здесь C 1 — произвольная постоянная. Если x (0) = 0,
График этой функции представлен на рис. 2.6. – он представляет собой кривую с насыщением.
Рис. 2.6. Концентрация вещества х в зависимости от времени. График уравнения 2.9.

Какие дифференциальные уравнения можно решать аналитически?
Лишь для ограниченных классов дифференциальных уравнений разработаны аналитические методы решения. Подробно они изучаются в курсах дифференциальных уравнений. Отметим основные из них/
1. Уравнения с разделяющимися переменными решаются в интегралах. К ним относятся оба приведенные выше примера.
2. Линейные дифференциальные уравнения (не обязательно автономные).
3. Некоторые специальные виды уравнений.
Решение линейного уравнения
Линейным дифференциальным уравнением 1-го порядка называют уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:
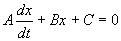
Здесь A, B, C — заданные непрерывные функции от t.
Пусть в некотором интервале изменения t A SYMBOL 185 f «Symbol» s 12 _ 0 . Тогда на него можно разделить все члены уравнения. При этом получим:
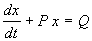
Eсли Q=0 , уравнение (2.12) называется однородным, если Q SYMBOL 185 f «Symbol» s 12 _ 0 – неоднородным.
Решим сначала однородное уравнение.
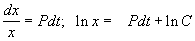
Общее решение линейного однородного уравнения имеет вид:
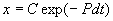
Видео:Биоинформатика и математическое моделирование. Лекция 4Скачать

Чтобы найти решение неоднородного уравнения применим метод вариации постоянной. Будем считать С неизвестной функцией t . Подставляя правую часть выражения (2.13) в уравнение (2.12), имеем:
Теперь С находим интегрированием: 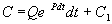
Итак, общее решение линейного неоднородного уравнения первого порядка:
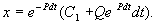
Таким образом, решение уравнения (2.12) представляет собой сумму двух слагаемых:
1) общее решение однородного уравнения (2.13) и
2) частное решение неоднородного уравнения, которое получается из общего решения, если С1 = 0.
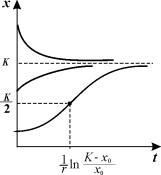
Рассмотрим еще один пример, который относится к классическим моделям математической экологии. Логистическое уравнение было предложено Ферхюльстом в 1838 г. Оно имеет вид:
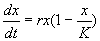
Это уравнение обладает двумя важными свойствами. При малых х численность х возрастает, при больших – приближается к определенному пределу К .
Уравнение (2.15) можно решить аналитически. Ход решения следующий. Произведем разделение переменных:
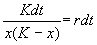
Представим левую часть в виде суммы и проинтегрируем
Переходя от логарифмов к переменным, получим:
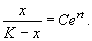
Здесь С – произвольная постоянная, которая определяется начальным значением численности x0 :
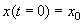
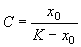
Подставим это значение С в формулу (2.17):
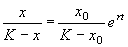
Отсюда получим решение – зависимость численности от времени:
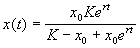
График функции (2.18) при разных начальных значениях численности популяции представлен на рис. 2.7.
Рис.2.7. Динамика численности в логистической модели 2.18
при разных начальных значениях численности

Если начальное значение х0 К/2, кривая роста имеет точку перегиба. Если х0 > К, численность со временем убывает.
В приведенных примерах в правой части уравнений стоят полиномы первой и второй степени. Если в правой части ‑ более сложная нелинейная функция, алгебраическое уравнение для стационарных значений может иметь несколько корней. Какое из этих решений реализуется в этом случае, будет зависеть от начальных условий.
В дальнейшем мы, как правило, не будем искать аналитическое решение для наших моделей. Для более сложных нелинейных уравнений это и невозможно. Однако важные заключения относительно свойств моделей можно сделать и на основании качественного их исследования, в первую очередь путем исследования устойчивости стационарных состояний и типов поведения системы вблизи этих состояний. При этом следует иметь в виду, что с помощью одного автономного дифференциального уравнения могут быть описаны только монотонные изменения переменной, и, следовательно, ни периодические, ни хаотические процессы не могут быть описаны. Для описания более сложного поведения необходимо либо переходить к системам большей размерности (2, 3 порядка и выше), либо вводить время в явном виде в правую часть уравнения. В Лекции 3 мы увидим, что дискретные уравнения и уравнения с запаздыванием могут описать и колебания, и динамический хаос.
ЛЕКЦИЯ 5
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙ НЕЛИНЕЙНЫХ СИСТЕМ ВТОРОГО ПОРЯДКА
Метод Ляпунова линеаризации систем в окрестности стационарного состояния. Примеры исследования устойчивости стационарных состояний моделей биологических систем. Уравнения Лотки. Уравнения Вольтерра. Метод функции Ляпунова
Пусть биологическая система описывается системой двух автономных дифференциальных уравнений второго порядка общего вида:

Стационарные значения переменных системы определяются из алгебраических уравнений:

Стационарные состояния соответствуют особым точкам дифференциального уравнения первого порядка, определяющего интегральные кривые:

Математический анализ поведения траекторий этой системы на фазовой плоскости связан с именами французского математика Анри Пуанкаре и русского математика и механика Александра Михайловича Ляпунова (1857-1918).
Ляпунов показал, что в большом числе случаев анализ устойчивости стационарного состояния нелинейной системы можно заменить анализом устойчивости системы, линеаризованной в окрестности стационарного состояния.
Рассмотрим характер поведения переменных при некотором небольшом отклонении системы от состояния равновесия. Введем вместо переменных x, y новые независимые переменные x , h , определив их как смещения относительно равновесных значений переменных

Подставив эти выражения в (5.1), получим:



Предположим, что функции P и Q непрерывны и имеют непрерывные производные не ниже первого порядка. Тогда мы можем разложить правые части уравнений (5.5) в ряд Тейлора по переменным x , h .


Учтем, что по определению особой точки
и отбросим в уравнениях (5.6) нелинейные члены. Получим систему линейных уравнений с постоянными коэффициентами — систему первого приближения:

Решение этой системы было рассмотрено в Лекции 4. Оно определяется корнями характеристического уравнения системы:

Ляпунов показал, что в случае, если оба корня уравнения (5.9):

имеют отличные от нуля действительные части, исследование уравнений первого приближения (5.8) всегда дает правильный ответ на вопрос о типе устойчивости состояния равновесия в системе (5.1). А именно:
· если оба корня имеют отрицательную действительную часть и, следовательно, все решения уравнений первого приближения (5.8) затухают, то состояние равновесия устойчиво;
· если хотя бы один корень имеет положительную действительную часть, то есть система (5.8) имеет нарастающие решения, то состояние равновесия неустойчиво.
Если действительные части обоих корней характеристического уравнения равны нулю или если один корень равен нулю, а другой отрицателен, то уравнения (5.8) не дают ответа на вопрос об устойчивости состояния равновесия, и необходимо рассматривать члены более высокого порядка малости в разложении в ряд Тейлора правых частей уравнений (5.6).
В случае, когда оба корня характеристического уравнения имеют отличные от нуля действительные части ( грубые с истемы), уравнение первого приближения определяют не только устойчивость стационарного состояния, но и характер фазовых траекторий в достаточно малой его окрестности.
Как и в случае линейных уравнений (Лекция 4) здесь возможны пять типов грубых состояний равновесия: устойчивый узел, неустойчивый узел, устойчивый фокус, неустойчивый фокус и седло. Для исследования типов состояний равновесий удобно пользоваться диаграммой, изображенной на рис. 4.11. Для системы (5.1):



Видео:Биоинформатика и математическое моделирование. Лекция 5Скачать

Грубым состояниям равновесия соответствуют все точки плоскости параметров s , D , лежащие вне оси D =0 и полуоси s =0, D >0.
Точкам оси D = 0 и полуоси s = 0, D >0 соответствуют негрубые состояния равновесия (негрубые особые точки). Их свойства могут быть изменены сколь угодно малыми изменениями правых частей уравнений (5.1) за счет сколь угодно малых изменений функций P(x,y), Q(x,y) и их производных. Поэтому характер негрубых состояний равновесия (в частности, устойчивость) уже не определяется значениями коэффициентов в правых частях уравнений первого приближения (5.8). В отличие от линейных систем, уже при небольших изменений в правых частях содержащихся там нелинейных членов может произойти качественное изменение фазового портрета — бифуркация.
1. Кинетические уравнения Лотки ( A . J . Lotka . Elements of Physical Biology, 1925)
Лоткой была исследована гипотетическая химическая реакция:
Модель очень простая и служит хорошей иллюстрацией применения исследования устойчивости стационарного состояния системы методом линеаризации.
Пусть в некотором объеме находится в избытке вещество А. Молекулы А с некоторой постоянной скоростью 
Запишем систему уравнений, описывающих реакцию:

Здесь x , y , B — концентрации химических компонентов. Первые два уравнения этой системы не зависят от B , поэтому их можно рассматривать отдельно. Рассмотрим стационарное решение системы:
Из этих условий получим систему алгебраических уравнений, связывающих равновесные концентрации 

Координаты особой точки:

Исследуем устойчивость этого стационарного состояния методом Ляпунова. Введем новые переменные x , h , характеризующие отклонения переменных от равновесных концентраций 

Линеаризованная система в новых переменных имеет вид:

Отметим, что величины отклонений от стационарных значений переменных x , h могут менять знак, в то время как исходные переменные x , y , являющиеся концентрациями, могут быть только положительными.
Запишем характеристическое уравнение системы (4.3):

Корни характеристического уравнения:

Фазовый портрет системы (5.13) изображен на рис. 5.1.
Рис. 5.1. Фазовый портрет системы 5.13.
а – устойчивый фокус ,
б – устойчивый узел.
При 
Таким образом, в описанной выше химической реакции возможны разные режимы изменения переменных в зависимости от соотношения величин констант скоростей. Если 

Рис. 5.2 Плоскость параметров для системы 5.14.
а – область устойчивого фокуса; б – область устойчивого узла
Соотношение параметров 
Рассмотрим плоскость параметров, где по оси абсцисс отложены значения константы k2, а по оси ординат – произведение k 0 k 1 . Парабола k 0 k 1 = 4 k 2 2 делит изображенную на рис. 5.2 плоскость параметров на две области – устойчивых узлов и устойчивых фокусов. Задавая те или иные значения параметров, можно получить колебательный и бесколебательный режимы изменения концентраций веществ x и y , и фазовый портрет системы, соответственно, будет собой представлять фокус (а) или узел (б), изображенные соответственно на рис 5.1 а, и 5.1 б.
Если в системе установятся стационарные концентрации веществ x и y , это приведет к установлению постоянной скорости прироста концентрации вещества В в третьем уравнении системы (5.13):

Ясно, что в действительности такая система реализоваться не может, так как в ней при t ® ¥ концентрация вещества В стремится к бесконечности. Однако система, подобная системе реакций Лотки, может представлять собой фрагмент более сложной химической системы. Исследованные нами уравнения правильно описывают поведение компонентов x и y , если приток вещества x (скорость его постоянна и равна k 0 ) осуществляется из большого «резервуара», а отток вещества y – в большой «резервуар» (значение В очень велико). При этих предположениях на малых промежутках времени (по сравнению с временем существенного изменения заполненности емкости B ) наше рассмотрение является вполне правомерным.
2. Модель Вольтерра
В качестве второго примера рассмотрим классическую модель взаимодействия видов, которая впервые была предложена В. Вольтерра в тридцатые годы XX века для объяснения периодических изменений числа особей, так называемую вольтерровскую модель «хищник-жертва». Более подробно модели взаимодействия видов мы рассмотрим в Лекции 9.
Пусть в некотором замкнутом районе живут хищники и жертвы, например, зайцы и волки. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Обозначим число зайцев (жертв) x, а число волков (хищников) – y . Так как количество пищи у зайцев неограниченно, мы можем предположить, что они размножаются со скоростью, пропорциональной их числу:

Если рождаемость зайцев превышает их смертность, e > 0. Выражение (5.16) соответствует автокаталитической реакции первого порядка.
Пусть убыль зайцев пропорциональна вероятности встречи зайца с волком, т.е. пропорциональна произведению численностей xy . Можно предположить по аналогии с бимолекулярными реакциями, где вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, что и количество волков нарастает тем быстрее, чем чаще происходят их встречи с зайцами, а именно, пропорционально xy .
Кроме того, имеет место процесс естественной смертности волков, причем скорость смертности пропорциональна их количеству.
Эти рассуждения приводят к системе уравнений для изменений численности зайцев-жертв x и волков-хищников y.

Покажем, что система уравнений (5.17) имеет на фазовой плоскости переменных xy ненулевую особую точку типа центр. Координаты этой особой точки 

Так как все параметры 



Рис. 5.3. Фазовый портрет системы 5.17. Особая точка типа «центр».
а – параметры системы: e x = 4, g xy = 0,3, e y = g yx = 0,4
б – параметры системы: e x =2, g xy = 0,3, e y = g yx = 0,4
Здесь x , h — отклонения 
Характеристическое уравнение системы (5.18):
Корни этого уравнения чисто мнимые:

Таким образом, исследование системы показывает, что траектории вблизи особой точки являются концентрическими эллипсами, а сама особая точка – центром. Рас c матриваемая модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной, и определяется параметрами системы (рис. 5.3).
Изменения численности жертвы и хищника во времени представляют собой колебания, причем колебания численности хищника отстают по фазе от колебаний жертв.
Как мы уже отмечали в Лекции 4, особая точка типа центр устойчива по Ляпунову, но не асимптотически. Покажем на данном примере, в чем это проявляется. Пусть колебания x ( t ) и y ( t ) происходят таким образом, что изображающая точка движется по фазовой траектории 1 (рис 5.3).
В момент, когда точка находится в положении М1, в систему добавляется извне некоторое число особей y такое, что изображающая точка переходит скачком из точки M 1 в точку M 2 . Если после этого систему предоставить самой себе, колебания x ( t ) , y ( t ) уже будут происходить с большими амплитудами, чем прежде, и изображающая точка будет двигаться по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии.
Рис. 5.4. Кривые численности зайца и рыси в Канаде
(по К. Вилли, В. Детье, 1974)
В дальнейшем мы рассмотрим модели, описывающие устойчивые колебательные режимы, и покажем, что на фазовой плоскости такие асимптотически устойчивые периодические движения описываются предельными циклами.
На рис. 5.4 кривые колебаний численности пушных зверей по данным компании Гудзонова залива о числе заготовленных шкурок. Во всех классических учебниках в течение многих лет колебательный характер этих изменений приводили как подтверждение гипотез, положенных в основу модели Вольтерра, которую мы только что рассмотрели. Действительно, периоды колебаний численности зайцев (жертв) и рысей (хищников) примерно одинаковы и составляют порядка 9 – 10 лет. При этом максимум численности зайцев опережает, как правило, максимум численности рысей на один год. Можно полагать, что мы видим регулярные колебания, осложненные случайными факторами, связанными с погодой и проч.
Однако возможна и другая интерпретация этих данных наблюдений на основе моделей детерминированного хаоса. О дискретных моделях такого типа мы уже говорили в Лекции 3. Непрерывные модели популяционной динамики, приводящие к детерминированному хаосу, мы рассмотрим в Лекции 9.
Видео:Модели биологических систем, описываемые одним дифференциальным уравнением первого порядкаСкачать

Серьезным недостатком рассмотренной модели Вольтерра является неустойчивость решений по отношению к малым случайным воздействиям, приводящим к изменению переменных. Кроме того, в силу «негрубости» этой системы произвольно малое изменение вида правых частей уравнений (величин параметров системы) приведет к изменению типа особой точки, и, следовательно, к изменению характера фазовых траекторий.
Поскольку природные системы подвергаются огромному количеству случайных воздействий, реалистическая модель должна быть по отношению к ним устойчивой. Поэтому негрубые системы не могут давать адекватное описание природных явлений.
Различные модификации рассмотренной нами системы, изученные самим Вольтерра и другими авторами, лишены этих недостатков. Наиболее широко известные из них будут рассмотрены в Лекции 9. Здесь мы остановимся на модели, которая учитывает самоограничение в росте обеих популяций. На ее примере видно, как может меняться характер решений при изменении параметров системы.
Итак, рассмотрим систему:

Система (5.19) отличается от ранее рассмотренной системы наличием в правых частях членов:
Эти члены отражают тот факт, что численность популяции жертв не может расти до бесконечности даже в отсутствие хищников в силу ограниченности пищевых ресурсов, ареала существования и проч. Такие же «самоограничения» накладываются на популяцию хищников.
Система имеет два стационарных решения: нулевое и ненулевое. Анализ показывает, что нулевое решение представляет собой неустойчивый узел. Рассмотрим систему алгебраических уравнений, решение которых дает координаты ненулевого стационарного состояния.

Корни характеристического уравнения системы, линеаризованной в окрестности особой точки:

Из выражения для характеристических чисел видно, что если выполнено условие

то численности хищников и жертв совершают во времени затухающие колебания. Система имеет особую точку – устойчивый фокус.
Рис. 5.5. Фазовый портрет системы 5.19
а – устойчивый фокус,
б – устойчивый узел,
При изменении знака неравенства на обратный точка становится устойчивым узлом.
И в том и в другом случае стационарное состояние асимптотически устойчиво, и решение устойчиво к малым изменениям правых частей уравнений. Таким образом, самоограничение популяции приводит к устойчивости ее численности.
Важно отметить, что простейшие вольтерровские модели, которые мы рассмотрели, не могут описывать устойчивые колебания с постоянными периодом и амплитудой. Для описания таких колебаний необходимы нелинейные модели, имеющие на фазовой плоскости предельный цикл . Они будут рассмотрены в Лекции 8.
МЕТОД ФУНКЦИЙ ЛЯПУНОВА ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ СТАЦИОНАРНОГО СОСТОЯНИЯ.
При аналитическом исследовании устойчивости стационарного состояния часто используется метод подбора функции, линии уровня которой представляют собой замкнутые траектории – «ловушки» для фазовых траекторий системы типа (5.1)
Этот метод применим к автономной системе уравнений n -го порядка

Он состоит в непосредственном исследовании устойчивости ее стационарного состояния при помощи подходящим образом подобранной функции Ляпунова 
Метод основан на двух теоремах.
Если существует дифференцируемая функция V ( x 1 ,…, xn ), удовлетворяющая в окрестности начала координат следующим условиям:
б)
причем 
то точка покоя системы (5.21) устойчива.
Если существует дифференцируемая функция V ( x 1 ,…, xn ), удовлетворяющая в окрестности начала координат следующим условиям:
a ) V ( x 1 ,…, xn ) = 0 и сколь угодно близко от начала координат имеются точки, в которых V ( x 1 ,…, xn ) > 0;
б)
причем 
то точка покоя системы (5.21) неустойчива.
С доказательством этих теорем можно познакомиться в книге Л.Э. Эльсгольц «Теория дифференциальных уравнений» или в других учебниках по теории дифференциальных уравнений.
Общего методы построения функции Ляпунова не существует. Однако для линейных автономных систем ее следует искать в виде:
и т.п., подбирая надлежащим образом коэффициенты a > 0 , b > 0. Для нелинейных систем a и b могут быть произвольных знаков.
1. Рассмотрим линейную систему:
Выберем функцию Ляпунова: V = x 2 + y 2 . Тогда
Это выражение всегда отрицательно при х ¹ 0 , т.к. в скобках стоят четные степени x . Следовательно, точка (0, 0) устойчива.
2. Рассмотрим систему уравнений, описывающую конкуренцию видов, численности которых x и y . Каждый из видов размножается в соответствии с логистическим законом, а при встрече (произведения в правых частях уравнений), численность как одного, так и другого вида уменьшается.

Исследуем стационарное состояние, соответствующее сосуществованию видов ( ` x , ` y ) – ненулевое для x и y . Его координаты:

В. Вольтерра показал, что стационарное состояние (5.23) устойчиво для параметров системы a > 0, b £ 1 , построив функцию Ляпунова:

Ее производная равна
и отрицательна при малых значениях коэффициентов a , b и x , y > 0. Доказательство приведено в книге В. Вольтерра. «Математическая теория борьбы за существование» (М., 1976)
Ризниченко Г.Ю., Рубин А.Б. Математические модели биологических продукционных процессов. М., изд. МГУ, 1993
Вольтерра В. Математическая теория борьбы за существование М., Наука, 1976
Эльсгольц Л.Э. Теория дифференциальных уравнений. М., Наука, 1971
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

💥 Видео
Решение системы дифференциальных уравнений методом ЭйлераСкачать

Модели, представленный системой двух дифференциальных уравненийСкачать

Урок 7.1 (теория) Система дифференциальных уравнений теплообмена и гидродинамикиСкачать

Уравнение Шредингера Стационарные состоянияСкачать

Системы дифференциальных уравнений. Метод исключенияСкачать

Системы дифференциальных уравнений. Метод исключения.Скачать

Системы дифференциальных уравненийСкачать

Биоинформатика и математическое моделирование. Лекция 3Скачать

ДУ Линейные системыСкачать

Матричные модели популяций. Модели, представленный системой двух дифференциальных уравненийСкачать

Системы дифференциальных уравнений. Часть 1Скачать

Исследование одного дифференциального уравнения (часть 1)Скачать