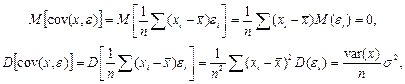Статистические свойства коэффициентов уравнения парной регрессии теорема гаусса маркова (7 видео)

Содержание

Предпосылки регрессионного анализа. Условия Гаусса-Маркова
Уравнение множественной регрессии. Теорема Гаусса – Маркова
Регрессионный анализ: теорема Гаусса — Маркова
🎬 Видео

Видео:Что поделать с мультиколлинеарностьюСкачать

Предпосылки регрессионного анализа. Условия Гаусса-Маркова

Глава 3. Свойства коэффициентов регрессии и проверка гипотез

Случайные составляющие коэффициентов регрессии

Величина Y в модели регрессии Y = a + b× X + e имеет две составляющие: неслучайную (a + b×X) и случайную (e).

Оценки коэффициентов регрессии (a; b)являются линейными функциями Y и теоретически их также можно представить в виде двух составляющих.

Воспользовавшись разложением показателей:

получим преобразованные соотношения для (a; b):

(3.1)

Таким образом, коэффициенты (a; b) разложены на две составляющие:

неслучайную, равную истинным значениям (a; b) и случайную, зависящую от e.

На практике нельзя разложить коэффициенты регрессии на составляющие, т.к. значения (a; b) или фактические значения e в выборке неизвестны.

Предпосылки регрессионного анализа. Условия Гаусса-Маркова

Линейная регрессионная модель с двумя переменными имеет вид:

где Y –объясняемая переменная, X – объясняющая переменная, e – случайный член.

Для того, чтобы регрессионный анализ, основанный на МНК давал наилучшие из всех возможных результаты, должны выполняться условия Гаусса-Маркова.

1.Математическое ожидание случайного члена в любом наблюдении должно быть равно нулю

2. Дисперсия случайного члена должна быть постоянной для всех наблюдений

3. Случайные члены должны быть статистически независимы (некоррелированы) между собой

4.Объясняющая переменнаяx_i естьвеличина неслучайная.

При выполнении условий Гаусса-Маркова модель называется классической нормальной линейной регрессионной моделью.

Наряду с условиями Гаусса-Маркова обычно предполагается, что случайный член распределен нормально, т.е. e_i

Замечание. Если случайный член имеет нормальное распределение, то требование некоррелированности случайных членов эквивалентно их независимости.

Рассмотрим подробнее условия и предположения, лежащие в основе регрессионного анализа.

Первое условие означает, что случайный член не должен иметь систематического смещения. Если постоянный член включен в уравнение регрессии, то это условие автоматически выполняется.

Второе условиеозначает, что дисперсия случайного члена в каждом наблюдении имеет только одно значение.

Под дисперсией s 2 имеется в виду возможное поведение случайного члена до того, как сделана выборка. Величина s 2 неизвестна, и одна из задач регрессионного анализа состоит в её оценке.

Условие независимости дисперсии случайного члена от номера наблюдения называется гомоскедастичностью (что означает одинаковый разброс). Зависимость дисперсии случайного члена от номера наблюдения называется гетероскедастичностью.

Характерные диаграммы рассеяния для двух случаев показаны на рис. 9,а и б соответственно.

Если условие гомоскедастичности не выполняется, то оценки коэффициентов регрессии будут неэффективными, хотя и несмещенными.

Существуют специальные методы диагностирования и устранения гетероскедастичности.

Третье условиеуказывает на некоррелированность случайных членов для каждых двух соседних наблюдений. Это условие часто нарушается, когда данные являются временными рядами. В случае, когда третье условие не выполняется, говорят об автокорреляции остатков.

Типичный вид данных при наличии автокорреляции показан на рис. 10.

Если условие независимости случайных членов не выполняется, то оценки коэффициентов регрессии, полученные по МНК, оказываются неэффективными,хотя и несмещенными.

Существуют методы диагностирования и устранения автокорреляции.

Четвертое условиео неслучайностиобъясняющей переменной является особенно важным.

Если это условие нарушается, то оценки коэффициентов регрессии оказываются смещенными и несостоятельными.

Нарушение этого условие может быть связано с ошибками измерения объясняющих переменных или с использованием лаговых переменных.

В регрессионном анализе часто вместо условия о неслучайности объясняющей переменной используется более слабое условие о независимости (некоррелированности) распределений объясняющей переменной и случайного члена.Получаемые при этом оценки коэффициентов регрессии обладают теми же основными свойствами, что и оценки, полученные при использовании условия о неслучайности объясняющей переменной.

Предположение о нормальности распределения случайного члена необходимо для проверки значимости параметров регрессии и для их интервального оценивания.

Теорема Гаусса-Маркова

Теорема Гаусса-Маркова. Если условия 1-4 регрессионного анализа выполняются, то оценки (a, b), сделанные с помощью МНК, являются наилучшими линейными несмещенными оценками, т.е. обладают следующими свойствами:

несмещенности: M(a) = a, M(b) = b, что означает отсутствие систематической ошибки в положении линии регрессии;

эффективности: имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, равную

;

состоятельности: , что означает, что при достаточно большом n оценки (a; b) близки к (a; b).

Для проверки выводов теоремы воспользуемся оценками (a, b) в виде разложения (3.1) и соотношением

Пусть x не случайная величина, тогда

Вычислим математическое ожидание и дисперсию оценок b, a:

Видео:10. Линейная регрессияСкачать

Уравнение множественной регрессии. Теорема Гаусса – Маркова

Почему же в практических приложениях оказались важными свойства оценок? Это связано с тем, что при моделировании реальных объектов, в том числе экономических, параметры являются не только числовыми коэффициентами при переменных, а несут на себе смысловую нагрузку, часто имеют размерность и по их величинам делают вывод о свойствах объекта.

Например, если модель (2.8) описывает зависимость расходов на потребление от располагаемого дохода, то параметр a1 есть предельные расходы по доходу и показывает, на сколько единиц изменяются расходы на потребление при увеличении дохода на одну единицу.

Теорема Гаусса – Маркова [1] формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

Несмотря на то, что Марков родился через год после смерти Гаусса, теорема была названа по их именам. Заслуга Гаусса – в разработке МНК, заслуга Маркова – в формулировке условий, при которых МНК позволяет получить состоятельные оценки.

Сформулируем постановку задачи. Мы имеем:

1) спецификацию модели в виде линейного уравнения множественной регрессии:

(5.20)

2) выборку из n наблюдений за поведением переменных модели:

(5.21)

Значения переменных в каждом наблюдении связаны между собой по правилу (5.20). Следовательно, в соответствие каждому наблюдению можно поставить уравнение:

(5.22)

Система уравнений (5.22) называется системой уравнений наблюдения или схемой Гаусса – Маркова.

Далее будем использовать следующие обозначения

– вектор наблюдений за эндогенной переменной; (5.23)

– вектор параметров линейной модели; (5.24)

(5.25)

В матрице X в первом столбце записана единица.

Это «псевдопеременная» при параметре. Эта единица появляется в матрице X только в тех случаях, когда спецификация модели содержит свободный параметр. Если на этапе спецификации этот параметр не был записан, то и в матрице X столбец из единиц отсутствует.

В компактной записи с учетом введенных обозначений система уравнений наблюдений (схема Гаусса – Маркова) имеет вид:

(5.26)

Задача заключается в том, чтобы найти:

1) значения состоятельных оценок параметров модели (5.20);
2) значения несмещенных ошибок оценок параметров;
3) оценку ошибки случайного возмущения;
4) оценку наилучшего прогноза с помощью модели (5.20);
5) оценку ошибки прогноза.

Теорема начинается с описания условий, которые накладываются на вектор случайных возмущений. Эти условия принято называть предпосылками теоремы Гаусса – Маркова.

Теорему условно можно разбить на две части: «если» и «тогда».

В первой части теоремы («если») формулируются условия на случайные возмущения, при выполнении которых МНК-оценки параметров линейной модели множественной регрессии отвечают свойствам несмещенности и эффективности. Эти условия принято называть предпосылками теоремы Гаусса – Маркова. Во второй части («тогда») формулируются оптимальные процедуры вычисления оценок параметров модели и основных функций этих параметров.

Теорема 5.1. «Если»:

1. Математическое ожидание случайных возмущений во всех наблюдениях равно нулю:

(5.27)

2. Дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе:

(5.28)

3. Ковариация между парами случайных возмущений в наблюдениях равны нулю (случайные возмущения в наблюдениях независимы):

(5.29)

4. Ковариация между вектором регрессоров и вектором случайных переменных равна нулю (регрессоры и случайные возмущения независимы):

(5.30)

«Тогда»: если матрица X (5.26) неколлинеарная (нет ни одного столбца, который можно было бы представить в виде линейной комбинации других его столбцов)

1. Наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется, как

(5.31)

Она соответствует методу наименьших квадратов.

2. Ковариационная матрица оценок параметров модели вычисляется, как

(5.32)

3. Дисперсия случайного возмущения равна

(5.33)

4. Наилучший прогноз по модели (5.20) в точке

вычисляется по правилу:

(5.34)

5. Ошибка прогноза эндогенной переменной равна

(5.35)

Учитывая важность теоремы Гаусса – Маркова для эконометрики, рассмотрим ее доказательство.

Доказательство. Воспользуемся методом наименьших квадратов:

(5.36) где

(5.37)

Подставляя (5.37) в (5.36) и выполнив перемножения, получим:

(5.38)

Для получения необходимого условия экстремума дифференцируем (5.38) по вектору:

(5.39)

Отсюда, система нормальных уравнений для вычисления оценок вектораимеет вид:

(5.40)

Тогда оценка вектораесть

Выражение (5.31) доказано.

Замечание. Требование неколлинеарности матрицы X обеспечивает существование матрицы . В противном случае процедура (5.31) неосуществима.

Покажем, что процедура (5.31) дает несмещенную оценку параметров модели множественной регрессии. Для этого необходимо вычислить математическое ожидание вектора

оценки:

(5.41)

Таким образом, несмещенность оценки (5.31) доказана. Отметим, что несмещенность достигнута в силу выполнения первой предпосылки теоремы Гаусса – Маркова.

Аналогичным образом доказывается справедливость выражения (5.32).

Остановимся более подробно на предпосылках теоремы Гаусса – Маркова.

Первая предпосылка (5.27) говорит о том, что во всех наблюдениях среднее значение (математическое ожидание) случайного возмущения равно нулю. Эта предпосылка отвечает за несмещенность параметров линейной модели множественной регрессии. Именно выполнение этой предпосылки обеспечило равенство нулю второго слагаемого в (5.41) и позволило получить несмещенные параметры модели.

Вторая предпосылка теоремы требует, чтобы во всех наблюдениях дисперсия случайного возмущения была одинаковой. Это свойство получило название свойства гомоскедастичности или однородности, или одинаковости дисперсий. В случае невыполнения данного условия говорят, что случайные возмущения в уравнениях наблюдения гетероскедастичные или неоднородные. Если случайные возмущения гетероскедастичные, то оценки параметров модели остаются несмещенными, но теряется эффективность оценки дисперсий параметров. Они, как правило, оказываются завышенными.

Третья предпосылка теоремы требует независимости случайных возмущений. Другими словами, каким бы не оказалось значение случайного возмущения в первом наблюдении, оно никак не сказывается на значениях случайного возмущения в любом другом наблюдении. Это свойство получило название неавтокоррелируемости случайных возмущений. Если это свойство не выполняется, то это так же сказывается на оценках дисперсий параметров модели. В этом случае дисперсии, как правило, занижены.

Четвертая предпосылка теоремы требует независимости случайных возмущений от значений регрессоров (экзогенных переменных). Как мы уже отмечали, рассматривая результат построения модели парной регрессии (5.9), невыполнение этого условия приводит к смещенности параметров модели. В тех случаях, когда значения регрессоров фиксированы, т.е. являются константами, эта предпосылка выполняется автоматически. Однако в ряде случаев регрессоры могут носить случайный характер. Например, если значения регрессоров в выборке есть результат измерений, или когда в качестве регрессора выступает лаговая эндогенная переменная.

Видео:Лекция 10. Основы регрессионного анализа. Линейная регрессия, теорема Гаусса МарковаСкачать

Регрессионный анализ: теорема Гаусса — Маркова

Как было отмечено выше, для получения наилучших оценок параметров регрессионного уравнения методом наименьших квадратов необходимо выполнение целого ряда условий, которые резюмированы в виде известной теоремы Гаусса — Маркова.

Теорема Гаусса — Маркова основана на выполнении следующих блоков предпосылок.

Блок 1. Предпосылки относительно регрессионной модели.

Предпосылка 1. Модель регрессии является линейной и корректно заданной (см. формулу (3.1)).

Предпосылка 2. Объем выборки должен быть больше, чем число оцениваемых параметров.

Предпосылка 3. Регрессионное уравнение линейно по своим параметрам.

Блок 2. Предпосылки относительно случайной компоненты.

Предпосылка 4. Математическое ожидание случайной компоненты равно нулю.

Предпосылка 5. Дисперсия случайной компоненты конечна и постоянна.

Предпосылка 6. Случайная компонента не является автокоррели- рованной.

Блок 3. Предпосылки относительно регрессоров.

Предпосылка 7. Значения регрессоров являются фиксированными в повторных выборках.

Предпосылка 8. Выборочная дисперсия каждого из регрессоров должна быть положительна и конечна.

Предпосылка 9. Отсутствует коллинеарность (совершенная линейная связь) между регрессорами.

Предпосылка 10. Отсутствует связь между любым из регрессоров и случайной компонентой.

Теорема Гаусса — Маркова: при выполнении указанных выше предпосылок оценки параметров линейного регрессионного уравнения, получаемые методом наименьших квадратов, являются несмещенными и эффективными в классе всех линейных несмещенных оценок.

Если при этом случайная ошибка е ₍ имеет нормальное распределение, то получаемые методом наименьших квадратов оценки параметров линейного регрессионного уравнения считаются лучшими в классе всех оценок.

Данная теорема является исключительно важным результатом, полученным для метода наименьших квадратов [1] .

Значение этой теоремы с прикладной точки зрения заключается в первую очередь в анализе выполнения ее предпосылок при проведении оценивания методом наименьших квадратов. Прокомментируем каждую из представленных выше предпосылок подробно и в качестве конкретного примера будем рассматривать спецификацию следующего уравнения:

Начнем с первого блока предпосылок, касающихся непосредственно самой регрессионной модели.

Предпосылка 1. Корректность задания регрессионной модели. Данная предпосылка свидетельствует в первую очередь о том, что выбранная спецификация модели имеет корректную математическую форму, а также все необходимые регрессоры в своем составе.

Говоря о корректности математической формы, имеется в виду, что если влияние какого-то регрессора на зависимую переменную является нелинейным, например описывается квадратом (парабола) или логарифмом, как в случае регрессоров Х₂ и Х₃ в уравнении (3.4). Если вместо необходимой нелинейной формы будет использоваться линейная, то это приведет к существенному смещению оценок параметров уравнения.

То же самое касается и пропуска важных регрессоров. Например, если какой-либо существенный регрессор Zпропущен в уравнении (3.4), то можно показать, что этот факт сделает оценивание параметров методом наименьших квадратов смещенным и несостоятельным, особенно если этот регрессор Zдовольно тесно коррелирован с включенными в уравнение регрессорами.

К сожалению, в общем случае мы никогда не знаем, какие регрессоры и в какой форме необходимо включать в регрессионное уравнение. Лишь частично проблему математической формы модели можно решать, проводя экспертный и описательный анализ ситуации, строя графики зависимостей переменных.

Кроме того, можно применять так называемый RESET-тест (англ. Regression Specification Error Test), предложенный в 1969 г. Дж. Рамсеем [2] . Этот тест позволяет формально определить, не пропущены ли в регрессионном уравнении какие-либо переменные, которые являются нелинейными преобразованиями (квадратами, кубами и пр.) уже включенных в рассматриваемое уравнение переменных.

Скажем несколько слов о процедуре RESET-теста. На первом шаге оценивается интересующее уравнение регрессии, из которого получаются подогнанные значения зависимой переменной У/. На втором шаге квадраты и (или) кубы этих подогнанных значений включаются в исследуемое уравнение, которое оценивается повторно. На третьем шаге производится статистическое сравнение исходно оцененного уравнения с уравнением, имеющим в своем составе квадраты или кубы подогнанных значений зависимой переменной.

Если выясняется, что включенные в модель на втором шаге различные степени Yj значимого влияния не оказывают, то делается вывод о том, что можно продолжать работать с линейной спецификацией модели; в противном случае лучше рассмотреть нелинейную спецификацию модели. Таким образом, нулевая гипотеза теста заключается в том, что адекватной является линейная спецификация модели, а альтернативная гипотеза — в том, что нелинейная спецификация более адекватна.

Необходимо правильно понимать логику данного теста: те принципиально иные переменные (регрессоры), которые стоило бы включить в уравнение, но которые мы не включили, нельзя обнаружить с помощью этого теста. Но с практической точки зрения этот тест часто дает понять, можно ли продолжать работать с линейной спецификацией или стоит рассмотреть какую-то нелинейную модификацию нашей регрессионной модели (хотя тест и не указывает, какую конкретно). Ниже на конкретном практическом примере продемонстрируем применение этого теста.

Предпосылка 2. Объем выборки. Данную предпосылку прокомментируем кратко. С математической точки зрения можно показать, что если количество наблюдений п в нашей выборке данных будет меньше, чем количество оцениваемых параметров р регрессионного уравнения (включая константу), то оценки этих параметров чисто математически не смогут быть рассчитаны. Поэтому для получения качественных оценок параметров необходимо, чтобы объем выборки в несколько раз превосходил число оцениваемых параметров.

Предпосылка 3. Линейность регрессионного уравнения по своим параметрам. Под линейностью регрессионного уравнения понимается в первую очередь его линейность по параметрам (3, а не по регрессорам X. Это достаточно важный момент, поскольку, как продемонстрировано на примере уравнения (3.4), сами регрессоры X могут быть представлены и в нелинейном виде (квадраты, кубы, логарифмы и пр.), но по оцениваемым параметрам уравнение должно быть линейно, т.е. коэффициенты (3 не могут быть, например, возведены в какую-то степень.

Теперь обсудим второй блок предпосылок, касающийся поведения случайной компоненты. Общий смысл предпосылок 4—6 относительно поведения случайной компоненты заключается в том, что ее поведение должно быть несистематическим, т.е. в поведении случайной компоненты не должно обнаруживаться никаких закономерностей. Другими словами, компонента е должна вести себя чисто случайным образом.

Предпосылка 4. Нулевое математическое ожидание случайной компоненты. Требование общей несистематичности поведения случайной компоненты означает, что, вообще говоря, в среднем мы не должны ожидать ее появления, т.е., поскольку данная компонента является единственным источником стохастики в классических линейных регрессионных моделях, в среднем она не должна вносить постоянного (систематического) смещения в уравнение модели. Это означает, что математическое ожидание (среднее) г должно быть равно нулю.

К счастью, математически метод наименьших квадратов автоматически выполняет это условие. Так, одним из свойств МНК является тот факт, что при его применении среднее значение остатков ё (т.е. конкретных реализаций случайной компоненты s) всегда равно нулю [3] .

Предпосылка 5. Постоянная дисперсия случайной компоненты. Еще

одним условием несистематичности поведения случайной компоненты является постоянство ее дисперсии. Это условие называется свойством гомоскедастичности (от гомо — одинаковый, скедастич- ность — разброс). Почему именно постоянство дисперсии? Дело заключается в том, что если дисперсия случайной компоненты не является постоянной, то, как правило, она меняется в зависимости от номера конкретного наблюдения в выборке, а значит, проявляет определенную закономерность поведения, чего необходимо избегать.

Отметим, что свойство непостоянства дисперсии случайной компоненты называется гетероскедастичностъю (от гетеро — разнородный, скедастичность — разброс). С практической точки зрения проблема гетероскедастичности наиболее характерна для пространственных данных. Источником же этой проблемы часто служат несопоставимые шкалы, в которых измеряются регрессоры и зависимая переменная. Например, если одна переменная измеряется в миллионах, а другая — в долях процентов, то, скорее всего, в модели, которая объединит эти переменные, будет наблюдаться гетероскеда- стичность остатков.

Заметим, что одним из эффективных приемов борьбы с этой проблемой является взятие натуральных логарифмов регрессоров в регрессионном уравнении. Логарифмическое преобразование позволяет очень эффективно приводить переменные к сопоставимым значениям. Однако это преобразование имеет и естественное ограничение: брать логарифмы можно только от переменных, которые принимают строго положительные значения.

Проблема гетероскедастичности является достаточно серьезной: если она присутствует в регрессионной модели, то оценки, получаемые по методу наименьших квадратов, хотя и остаются состоятельными и несмещенными, становятся неэффективными. Кроме того, гетероскедастичность приводит к искажению результатов теста на индивидуальную статистическую значимость коэффициентов (оценок параметров) исследуемого регрессионного уравнения.

На сегодняшний день разработан целый ряд тестов на гетероскедастичность, наболее известные — тест Голдфельда — Квандта, тест Бройша — Пагана, тест Уайта и др. [4]

Отметим, что проблема гетероскедастичности более характерна для пространственных данных. Ниже на конкретном примере мы проиллюстрируем процедуру проверки этой предпосылки.

Предпосылка 6. Случайная компонента не должна быть автокор- релирована. Проблема автокорреляции (от авто — само, корреляция — связь) — еще один из возможных аспектов систематичности поведения случайной компоненты. Она заключается в том, что для разных номеров наблюдений i и j соответствующие значения случайной компоненты s,. и s_y. оказываются связанными между собой (значение коэффициента корреляции между ними не равно нулю, сог (е,, ?у) Ф 0).

Последствия наличия автокорреляции в регрессионном уравнении схожи с последствиями гетероскедастичности: автокорреляция делает оценки метода наименьших квадратов неэффективными [5] . Это означает, что результаты теста на индивидуальную статистическую значимость оценок коэффициентов регрессии также будут искажены.

Отметим, что проблема автокорреляции более характерна для временных рядов, чем для пространственных данных. Для определения наличия автокорреляции в регрессионной модели был разработан ряд тестов, например тест Бройша — Годфри. Кроме того, эффективным инструментом для решения этой проблемы является автокорреляционная функция. Применение этого инструментария будет рассмотрено в гл. 5.

Третий блок предпосылок касается поведения самих регрессоров в модели.

Предпосылка 7. Значения регрессоров являются фиксированными в повторных выборках. Это довольно непростая с точки зрения теории регрессионного моделирования предпосылка, поэтому мы не будем подробно на ней останавливаться. Отметим только, что она еще раз подтверждает тот факт, что в классическом регрессионном уравнении случайная компонента является единственным источником стохастики, а регрессоры и зависимая переменная — неслучайные.

Предпосылка 8. Положительность и конечность выборочной дисперсии каждого из регрессоров. Фактически эта предпосылка говорит о том, что ни один из регрессоров не должен иметь все одинаковые значения. Если это требование не выполняется, то регрессор перестает быть переменной и превращается в константу. Однако технически это приводит к невозможности расчета оценок параметров регрессионного уравнения, так как константа в модели уже присутствует.

Предпосылка 9. Отсутствует коллинеарность (совершенная линейная связь) между регрессорами. Данная предпосылка по своей логике похожа на предыдущую. Под коллинеарностью (совершенной коллинеарностью) понимается наличие в регрессионном уравнении линейной зависимости между двумя или более регрессорами. Напомним, что линейная связь между переменными означает, что коэффициент корреляции между такими переменными равен +1 или — 1.

Математически можно показать, что в этом случае оценки методом наименьших квадратов не могут быть рассчитаны.

Однако с практической точки зрения серьезную проблему представляет ситуация мультиколлинеарности (англ, multicollinearity), когда коэффициент корреляции между некоторыми регрессорами в модели не равен, но очень близок по модулю к единице. В этом случае формально оценки МНК могут быть рассчитаны, но само присутствие этого эффекта в модели оказывает негативное влияние на качество ее оценивания. Например, оценки коэффициентов становятся очень чувствительными к небольшим изменениям (исключению или включению нескольких наблюдений) в используемом для оценивания наборе данных. Кроме того, мультиколлинеарность также увеличивает стандартные ошибки оцениваемых коэффициентов.

На сегодняшний день разработан целый ряд тестов на мультиколлинеарность. Мы рассмотрим только два из них — анализ корреляционной матрицы и VIF-тест.

Начнем с корреляционной матрицы. Перед проведением эконометрического анализа рекомендуется изучить значения коэффициентов попарных корреляций между используемыми регрессорами, для чего стандартными средствами любого программного пакета строится матрица попарных корреляций (см. пример ниже). Если при анализе этой матрицы обнаружится, что какие-то коэффициенты по модулю больше, чем 0,98, то это является признаком очень тесной линейной связи между соответствующими регрессорами и может стать причиной мультиколлинеарности.

После оценивания регрессионного уравнения полезно провести формальный тест. Один из простейших вариантов — использовать так называемый VIF-тест (от англ. Variance Inflation Factor, VIF — коэффициент «вздутия» дисперсии), не являющийся статистическим и в рамках которого просто рассчитываются коэффициенты роста («вздутия») дисперсии оценок параметров регрессионного уравнения, который произошел вследствие возможного присутствия проблемы мультиколлинеарности. Считается, что если VIF- значения меньше 10, то проблема мультиколлинеарности в регрессии не наблюдается.

Можно использовать и прочие тесты, такие как тест Л. Кляйна, Феррара — Глобера и др. При этом при обнаружении проблемы мультиколлинеарности стараются:

• либо совсем избавиться от одного или нескольких тесно связанных с другими регрессоров;
• либо посредством, например, факторного анализа заменить тесно коррелированные регрессоры на их некоторую линейную комбинацию или другой регрессор;

• либо применять специальные техники получения оценок регрессионного уравнения (такие как, например, ридж-регрессия или лассо-регрессия).

Предпосылка 10. Отсутствие связи между любым из регрессоров и случайной компонентой. Это тоже довольно непростая предпосылка, касающаяся теории эконометрического анализа. Проблема снова (как и при обсуждении предпосылки 1) заключается в пропуске каких-то важных регрессоров, которые мы не включили в свое регрессионное уравнение по причине либо их неизмеримости, либо недоступности данных по ним, либо потому, что не учли их возможное влияние на исследуемую зависимую переменную.

Говоря не очень формально, все пропущенные (неучтенные) регрессоры скапливаются в случайной компоненте и продолжают неявно влиять на зависимую переменную. Если при этом эти пропущенные регрессоры одновременно коррелированы и с учтенными в модели регрессорами, то возникает так называемая проблема эндогенности. Эта проблема весьма серьезна и приводит к несостоятельности МНК-оценок регрессионного уравнения. Подробное обсуждение этой проблемы в силу ее сложности выходит за рамки настоящего пособия, поэтому ограничимся лишь общей рекомендацией, которая поможет избежать этой проблемы: при построении регрессионной модели набор используемых регрессоров необходимо составлять таким образом, чтобы он был максимально полным и разнообразным (в рамках сохранения экономической логики модели), т.е. в состав регрессоров необходимо включать такие переменные, которые максимально разносторонне смогут объяснить поведение зависимой переменной.

В завершение темы необходимо сказать следующее. С одной стороны, как гласит теорема Гаусса — Маркова, выполнение указанных выше предпосылок позволяет получать максимально качественные (из возможных на имеющейся выборке) оценки параметров регрессионного уравнения. С другой стороны, удовлетворения только этих предпосылок недостаточно для построения адекватной регрессионной модели. Поэтому дальше перейдем к краткому обсуждению применения инструментария математической статистики в регрессионном анализе.