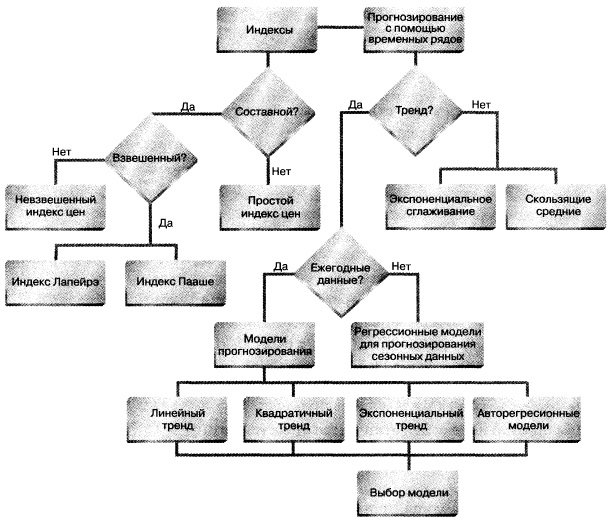
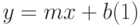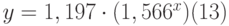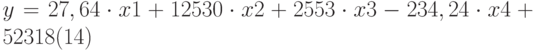В рамках своей диссертации «Модель прогнозирования по выборке максимального подобия» мне нужно было делать обзор моделей прогнозирования. Кроме обзора, я сделала вариант классификации, который мне тогда не очень удался. Классификацию уже немного поправила, теперь хочется разобраться в существующих моделях прогнозирования временных рядов. Такие модели называют стохастическими моделями (stochastic models).
По оценке некто Тихонова в его «Прогнозировании в условиях рынка» на сегодняшний день (2006 год) существует около 100 методов и моделей прогнозирования. Эта оценка звучит бредово, я полно разбирала ее! Давайте теперь вместе разберемся, какие же модели прогнозирования временных рядов существуют на сегодняшний день.
- Регрессионные модели прогнозирования
- Авторегрессионные модели прогнозирования (ARIMAX, GARCH, ARDLM)
- Модели экспоненциального сглаживания (ES)
- Модель по выборке максимального подобия (MMSP)
- Модель на нейронных сетях (ANN)
- Модель на цепях Маркова (Markov chains)
- Модель на классификационно-регрессионных деревьях (CART)
- Модель на основе генетического алгоритма (GA)
- Модель на опорных векторах (SVM)
- Модель на основе передаточных функций (TF)
- Модель на нечеткой логике (FL)
- Что еще.
- Регрессионные модели прогнозирования
- Авторегрессионные модели прогнозирования
- Модели экспоненциального сглаживания
- Модель по выборке максимального подобия
- Модель на нейронных сетях
- Модель на цепях Маркова
- Модель на классификационно-регрессионных деревьях
- Модель на основе генетического алгоритма
- Модель на опорных векторах
- Модель на основе передаточных функций
- Модель на нечеткой логике
- Итого
- Анализ временных рядов
- Прогнозирование. Регрессионный анализ, его реализация и прогнозирование
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- Сущность метода регрессионного анализа
- Линейная регрессия
- Нелинейная регрессия
- Множественная регрессия
- Использование функций регрессии
- Правила ввода функций
- Линия тренда
- Простая линейная регрессия
- Экспоненциальная регрессия
- Множественная линейная регрессия
- ЗАДАНИЕ
- 🔥 Видео
Регрессионные модели прогнозирования
Регрессионные модели прогнозирования одни из старейших, однако нельзя сказать, что она нынче очень популярны. Регрессионными моделями являются:
- Простая линейная регрессия (linear regression)
- Множественная регрессия (multilple regression)
- Нелинейная регрессия (nonlinear regression)
Лучшая книга по регрессии — архигениальная книга — Draper N., Smith H. Applied regression analysis. Ее можно скачать в сети в djvu. Лучше читать в английском варианте, написано в высшей степени для людей.
Авторегрессионные модели прогнозирования
Это широчайший и один из двух наиболее широко применимых классов моделей! Книг по этим моделям много, примеров применения много.
- ARIMAX (autoregression integrated moving average extended), об этом написано чрезвычайно много. Основой основ является книга Box, George and Jenkins, Gwilym (1970) Time series analysis: Forecasting and control. Лучше читать на английском!
- GARCH (generalized autoregressive conditional heteroskedasticity), здесь множество модификаций FIGARCH, NGARCH, IGARCH, EGARCH, GARCH-M.
- ARDLM (autoregression distributed lag model), об этом только в учебниках по эконометрике.
Вопрос к аудитории: посоветуйте хорошую и понятную (!) книгу/статью по GARCH и MLE.
Модели экспоненциального сглаживания
- Экспоненциальное сглаживание (exponential smoothing)
- Модель Хольта или двойное экспоненциальное сглаживание (double exponential smoothing)
- Модель Хольта-Винтерса или тройное экспоненциальное сглаживание (triple exponential smoothing)
По всем трем моделям лучшая из мною читанного статья Prajakta S.K. Time series Forecasting using Holt-Winters Exponential Smoothing.
Модель по выборке максимального подобия
Это моя модель (model on the most similar pattern), на ряде задач показывает высокую эффективность. К рядам FOREX и бирж применять не стоит, проверяли, работает неважно. Ее описание можно найти в диссертации по ссылке выше, кроме того, можно скачать пример реализации в MATLAB.
Модель на нейронных сетях
Вторая из двух наиболее популярных моделей прогнозирования временных рядов. Лучшая книга с примерами, на мой вкус, Хайкин С. Нейронные сети: полный курс. Книгу с примерами в MATLAB можно скачать по ссылке.
Модель на цепях Маркова
Модель на цепях Маркова фигурирует в множестве обзоров, однако мне не удалось найти ни хорошей книги, ни хорошей статьи о ее конкретном применении для прогнозирования временных рядов. Сама эту модель разбирала в курсе теории надежности (учебник Гнеденко), принцип ее расчета хорошо понимаю, кроме того, читала, что ее часто применяют для моделирования финансовых временных рядов.
Вопрос к аудитории: посоветуйте хорошую и понятную (!) книгу/статью по применению цепей Маркова для прогнозирования временных рядов.
Модель на классификационно-регрессионных деревьях
Вот тут материалов немного, но они есть. В частности, неплохая статья по применению этой модели для прогнозирования Hannes Y.Y., Webb P. Classification and regression trees: A User Manual for IdentifyingIndicators of Vulnerability to Famine and Chronic Food Insecurity.
Модель на основе генетического алгоритма
Это странный зверь, такого рода решения я называю «иезуитскими», потому что кажется, что они рождены только для обоснования научной новизны, однако эффективность их невысока. Например, генетический алгоритм применяется для решения задач оптимизации (поиска экстремума), однако некоторые приплели его к прогнозированию временных рядов. Найти внятного материала по этой теме мне не удалось.
Вопрос к аудитории: посоветуйте хорошую и понятную (!) книгу/статью по применению генетического алгоритма для прогнозирования временных рядов.
Модель на опорных векторах
Модель на основе передаточных функций
Модель на нечеткой логике
Все эти модели принадлежат, на мой вкус, классу иезуитских. Например, опорные векторы (SVM) применяется в основном для задач классификации. Нечеткая логика где только не применяется, однако найти ее понятно описанное применение для прогнозирования временных рядов мне не удалось. Хотя в обзорах специалисты почти всегда ее указывают.
Итого
Моделей мы наберем с десяток, со всеми модификациями — два десятка. Хотелось бы, чтобы в комментариях вы не только высказывали мнение, а по возможности делали полезные ссылки на понятные материалы. Лучше на английском!
PS. Всех любителей FOREX и всякого рода бирж большая просьба не долбится ко мне в личку! Вы мне ужасно надоели!
Видео:Временные ряды и прогнозированиеСкачать

Анализ временных рядов
В трех предыдущих заметках описаны регрессионные модели, позволяющие прогнозировать отклик по значениям объясняющих переменных. В настоящей заметке мы покажем, как с помощью этих моделей и других статистических методов анализировать данные, собранные на протяжении последовательных временных интервалов. В соответствии с особенностями каждой компании, упомянутой в сценарии, мы рассмотрим три альтернативных подхода к анализу временных рядов. [1]
Материал будет проиллюстрирован сквозным примером: прогнозирование доходов трех компаний. Представьте себе, что вы работаете аналитиком в крупной финансовой компании. Чтобы оценить инвестиционные перспективы своих клиентов, вам необходимо предсказать доходы трех компаний. Для этого вы собрали данные о трех интересующих вас компаниях — Eastman Kodak, Cabot Corporation и Wal-Mart. Поскольку компании различаются по виду деловой активности, каждый временной ряд обладает своими уникальными особенностями. Следовательно, для прогнозирования необходимо применять разные модели. Как выбрать наилучшую модель прогнозирования для каждой компании? Как оценить инвестиционные перспективы на основе результатов прогнозирования?
Обсуждение начинается с анализа ежегодных данных. Демонстрируются два метода сглаживания таких данных: скользящее среднее и экспоненциальное сглаживание. Затем демонстрируется процедура вычисления тренда с помощью метода наименьших квадратов и более сложные методы прогнозирования. В заключение, эти модели распространяются на временные ряды, построенные на основе ежемесячных или ежеквартальных данных.
Скачать заметку в формате Word или pdf, примеры в формате Excel
Прогнозирование в бизнесе
Поскольку экономические условия с течением времени изменяются, менеджеры должны прогнозировать влияние, которое эти изменения окажут на их компанию. Одним из методов, позволяющих обеспечить точное планирование, является прогнозирование. Несмотря на большое количество разработанных методов, все они преследуют одну и ту же цель — предсказать события, которые произойдут в будущем, чтобы учесть их при разработке планов и стратегии развития компании.
Современное общество постоянно испытывает необходимость в прогнозировании. Например, чтобы выработать правильную политику, члены правительства должны прогнозировать уровни безработицы, инфляции, промышленного производства, подоходного налога отдельных лиц и корпораций. Чтобы определить потребности в оборудовании и персонале, директора авиакомпаний должны правильно предсказать объем авиаперевозок. Для того чтобы создать достаточное количество мест в общежитии, администраторы колледжей или университетов хотят знать, сколько студентов поступят в их учебное заведение в следующем году.
Существуют два общепринятых подхода к прогнозированию: качественный и количественный. Методы качественного прогнозирования особенно важны, если исследователю недоступны количественные данные. Как правило, эти методы носят весьма субъективный характер. Если статистику доступны данные об истории объекта исследования, следует применять методы количественного прогнозирования. Эти методы позволяют предсказать состояние объекта в будущем на основе данных о его прошлом. Методы количественного прогнозирования разделяются на две категории: анализ временных рядов и методы анализа причинно-следственных зависимостей.
Временной ряд — это набор числовых данных, полученных в течение последовательных периодов времени. Метод анализа временных рядов позволяет предсказать значение числовой переменной на основе ее прошлых и настоящих значений. Например, ежедневные котировки акций на Нью-Йоркской фондовой бирже образуют временной ряд. Другим примером временного ряда являются ежемесячные значения индекса потребительских цен, ежеквартальные величины валового внутреннего продукта и ежегодные доходы от продаж какой-нибудь компании.
Методы анализа причинно-следственных зависимостей позволяют определить, какие факторы влияют на значения прогнозируемой переменной. К ним относятся методы множественного регрессионного анализа с запаздывающими переменными, эконометрическое моделирование, анализ лидирующих индикаторов, методы анализа диффузионных индексов и других экономических показателей. Мы расскажем лишь о методах прогнозирования на основе анализа временных рядов.
Компоненты классической мультипликативной модели временных рядов
Основное предположение, лежащее в основе анализа временных рядов, состоит в следующем: факторы, влияющие на исследуемый объект в настоящем и прошлом, будут влиять на него и в будущем. Таким образом, основные цели анализа временных рядов заключаются в идентификации и выделении факторов, имеющих значение для прогнозирования. Чтобы достичь этой цели, были разработаны многие математические модели, предназначенные для исследования колебаний компонентов, входящих в модель временного ряда. Вероятно, наиболее распространенной является классическая мультипликативная модель для ежегодных, ежеквартальных и ежемесячных данных. Для демонстрации классической мультипликативной модели временных рядов рассмотрим данные о фактических доходах компании Wm.Wrigley Jr. Company за период с 1982 по 2001 годы (рис. 1).
Рис. 1. График фактического валового дохода компании Wm.Wrigley Jr. Company (млн. долл. в текущих ценах) за период с 1982 по 2001 годы
Как видим, на протяжении 20 лет фактический валовой доход компании имел возрастающую тенденцию. Эта долговременная тенденция называется трендом. Тренд — не единственный компонент временного ряда. Кроме него, данные имеют циклический и нерегулярный компоненты. Циклический компонент описывает колебание данных вверх и вниз, часто коррелируя с циклами деловой активности. Его длина изменяется в интервале от 2 до 10 лет. Интенсивность, или амплитуда, циклического компонента также не постоянна. В некоторые годы данные могут быть выше значения, предсказанного трендом (т.е. находиться в окрестности пика цикла), а в другие годы — ниже (т.е. быть на дне цикла). Любые наблюдаемые данные, не лежащие на кривой тренда и не подчиняющиеся циклической зависимости, называются иррегулярными или случайными компонентами. Если данные записываются ежедневно или ежеквартально, возникает дополнительный компонент, называемый сезонным. Все компоненты временных рядов, характерных для экономических приложений, приведены на рис. 2.
Рис. 2. Факторы, влияющие на временные ряды
Классическая мультипликативная модель временного ряда утверждает, что любое наблюдаемое значение является произведением перечисленных компонентов. Если данные являются ежегодными, наблюдение Yi, соответствующее i-му году, выражается уравнением:
где Ti — значение тренда, Ci — значение циклического компонента в i-ом году, Ii — значение случайного компонента в i-ом году.
Если данные измеряются ежемесячно или ежеквартально, наблюдение Yi, соответствующее i-му периоду, выражается уравнением:
где Ti — значение тренда, Si — значение сезонного компонента в i-ом периоде, Ci — значение циклического компонента в i-ом периоде, Ii — значение случайного компонента в i-ом периоде.
На первом этапе анализа временных рядов строится график данных и выявляется их зависимость от времени. Сначала необходимо выяснить, существует ли долговременное возрастание или убывание данных (т.е. тренд), или временной ряд колеблется вокруг горизонтальной линии. Если тренд отсутствует, то для сглаживания данных можно применить метод скользящих средних или экспоненциального сглаживания.
Сглаживание годовых временных рядов
В сценарии мы упомянули о компании Cabot Corporation. Имея штаб-квартиру в Бостоне, штат Массачусеттс, она специализируется на производстве и продаже химикатов, строительных материалов, продуктов тонкой химии, полупроводников и сжиженного природного газа. Компания имеет 39 заводов в 23 странах. Рыночная стоимость компании составляет около 1,87 млрд. долл. Ее акции котируются на Нью-Йоркской фондовой бирже под аббревиатурой СВТ. Доходы компании за указанный период приведены на рис. 3.
Рис. 3. Доходы компании Cabot Corporation в 1982–2001 годах (млрд. долл.)
Как видим, долговременная тенденция повышения доходов затемнена большим количеством колебаний. Таким образом, визуальный анализ графика не позволяет утверждать, что данные имеют тренд. В таких ситуациях можно применить методы скользящего среднего или экспоненциального сглаживания.
Скользящие средние. Метод скользящих средних весьма субъективен и зависит от длины периода L, выбранного для вычисления средних значений. Для того чтобы исключить циклические колебания, длина периода должна быть целым числом, кратным средней длине цикла. Скользящие средние для выбранного периода, имеющего длину L, образуют последовательность средних значений, вычисленных для последовательностей длины L. Скользящие средние обозначаются символами MA(L).
Предположим, что мы хотим вычислить пятилетние скользящие средние значения по данным, измеренным в течение n = 11 лет. Поскольку L = 5, пятилетние скользящие средние образуют последовательность средних значений, вычисленных по пяти последовательным значениям временного ряда. Первое из пятилетних скользящих средних значений вычисляется путем суммирования данных о первых пяти годах с последующим делением на пять:
Второе пятилетнее скользящее среднее вычисляется путем суммирования данных о годах со 2-го по 6-й с последующим делением на пять:
Этот процесс продолжается, пока не будет вычислено скользящее среднее для последних пяти лет. Работая с годовыми данными, следует полагать число L (длину периода, выбранного для вычисления скользящих средних) нечетным. В этом случае невозможно вычислить скользящие средние для первых (L – 1)/2 и последних (L – 1)/2 лет. Следовательно, при работе с пятилетними скользящими средними невозможно выполнить вычисления для первых двух и последних двух лет. Год, для которого вычисляется скользящее среднее, должен находиться в середине периода, имеющего длину L. Если n = 11, a L = 5, первое скользящее среднее должно соответствовать третьему году, второе — четвертому, а последнее — девятому. На рис. 4 показаны графики 3- и 7-летних скользящих средних, вычисленные для доходов компании Cabot Corporation за период с 1982 по 2001 годы.
Рис. 4. Графики 3- и 7-летних скользящих средних, вычисленные для доходов компании Cabot Corporation
Обратите внимание на то, что при вычислении трехлетних скользящих средних проигнорированы наблюдаемые значения, соответствующие первому и последнему годам. Аналогично при вычислении семилетних скользящих средних нет результатов для первых и последних трех лет. Кроме того, семилетние скользящие средние намного больше сглаживают временной ряд, чем трехлетние. Это происходит потому, что семилетним скользящим средним соответствует более долгий период. К сожалению, чем больше длина периода, тем меньшее количество скользящих средних можно вычислить и представить на графике. Следовательно, больше семи лет для вычисления скользящих средних выбирать нежелательно, поскольку из начала и конца графика выпадет слишком много точек, что исказит форму временного ряда.
Экспоненциальное сглаживание. Для выявления долговременных тенденций, характеризующих изменения данных, кроме скользящих средних, применяется метод экспоненциального сглаживания. Этот метод позволяет также делать краткосрочные прогнозы (в рамках одного периода), когда наличие долговременных тенденций остается под вопросом. Благодаря этому метод экспоненциального сглаживания обладает значительным преимуществом над методом скользящих средних.
Метод экспоненциального сглаживания получил свое название от последовательности экспоненциально взвешенных скользящих средних. Каждое значение в этой последовательности зависит от всех предыдущих наблюдаемых значений. Еще одно преимущество метода экспоненциального сглаживания над методом скользящего среднего заключается в том, что при использовании последнего некоторые значения отбрасываются. При экспоненциальном сглаживании веса, присвоенные наблюдаемым значениям, убывают со временем, поэтому после выполнения вычислений наиболее часто встречающиеся значения получат наибольший вес, а редкие величины — наименьший. Несмотря на громадное количество вычислений, Excel позволяет реализовать метод экспоненциального сглаживания.
Уравнение, позволяющее сгладить временной ряд в пределах произвольного периода времени i, содержит три члена: текущее наблюдаемое значение Yi, принадлежащее временному ряду, предыдущее экспоненциально сглаженное значение Ei–1 и присвоенный вес W.
где Ei – значение экспоненциально сглаженного ряда, вычисленное для i-го периода, Ei–1 – значение экспоненциально сглаженного ряда, вычисленное для (i – 1)-гo периода, Yi – наблюдаемое значение временного ряда в i-ом периоде, W – субъективный вес, или сглаживающий коэффициент (0 
Если при аппроксимации временного ряда с помощью метода наименьших квадратов первое наблюдение расположить в начале координат, поставив его в соответствие значению X = 0, интерпретация коэффициентов упрощается. Все последующие наблюдения получают целочисленные номера: 1, 2, 3, так что n-е (последнее) наблюдение будет иметь номер n – 1. Например, если временной ряд записывается на протяжении 20 лет, первый год обозначается цифрой 0, второй— цифрой 1, третий — цифрой 2 и так далее, а последний (20-й) год — числом 19.
В сценарии была упомянута компания Wm. Wrigley Jr. Company, являющаяся крупнейшим производителем жевательной резинки в США. Акции компании котируются на Нью-Йоркской фондовой бирже под аббревиатурой WWY. Рыночная стоимость компании составляет 13 млрд. долл. Фактические доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах приведены на рис. 7. Затем с помощью индекса потребительских цен (Consumer Price Index — CPI), вычисляемого Бюро статистики Министерства труда США, фактические доходы были преобразованы в реальные. Для этого следует умножить величину фактического дохода на коэффициент 100/CPI.
Рис. 7. Фактические и реальные доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах
Обозначим последовательные значения переменной X с помощью целых чисел от 0 до 19, а затем выполним регрессионный анализ с помощью Пакета анализа (рис. 8).
Рис. 8. Модель линейной регрессии для предсказания реального дохода компании Wm. Wrigley Jr.; построена с помощью Пакета анализа Excel
Уравнение линейной регрессии имеет следующий вид (см. ячейки Е17, Е18 на рис. 8): Ŷi = 498,656 + 45,485Хi, где началом координат является 1982 год, а шаг переменной X равен одному году. Регрессионные коэффициенты интерпретируются следующим образом:
- Сдвиг b0 = 498,656 представляет собой предсказанное среднее значение реальных доходов компании Wm. Wrigley Jr. Company в 1982 году.
- Наклон b1 = 45,485 представляет собой предсказанное увеличение реальных доходов компании в среднем на 45,485 млн. долл. в год.
Линия тренда и временной ряд реальных доходов показаны на рис. 9. График можно построить на основании уравнения линейной регрессии (колонка D; рис. 9а) или простым добавлением линии тренда на ранее построенный график доходов (рис. 9б). Видно, что на протяжении ряда лет доходы компании линейно возрастали. Скорректированный коэффициент r 2 равен 0,966 (ячейка Е6 на рис. 8). Следовательно, все изменения реальных доходов хорошо описываются линейным трендом. Возникает вопрос: а нельзя ли выбрать еще более точную модель? Для ответа на него рассмотрим еще две модели — квадратичную и экспоненциальную.
Рис. 9. Линия тренда реальных доходов компании Wm. Wrigley Jr., вычисленная с помощью метода наименьших квадратов, построенная: (а) на основании уравнения линейной регрессии; (б) добавлением линии тренда на график
Модель квадратичного тренда, или полиномиальная модель второй степени является простейшей нелинейной моделью, применяемой для прогнозирования: 
где b0 – оценка сдвига отклика Y, b1 – оценка линейного эффекта, b2 – оценка квадратичного эффекта.
Построим квадратичный тренд путем добавления линии тренда на график с исходными данными (рис. 10).
Рис. 10. График квадратичного тренда для предсказания реальных доходов компании Wm. Wrigley Jr.
Как показано на рис. 10, уравнение линейной регрессии: Y =513,05 + 40,686Х + 0,2526Х 2 , где началом координат является 1982 год, а шаг переменной X равен одному году. Этот график аппроксимирует временной ряд почти так же, как и линейный тренд. Скорректированный коэффициент r 2 равен 0,965 (рис. 11), а t-статистика, учитывающая вклад квадратичного эффекта, равна 0,656 (соответствующее р-значение равно 0,521).
Рис. 11. Модель квадратичного тренда реальных годовых доходов
Модель экспоненциального тренда. Если временной ряд является возрастающим, а относительное изменение данных — постоянным, можно применять модель экспоненциального тренда. Учитывая сложность формул ограничимся только графическим анализом. Для этого на график с исходными данными добавим линию экспоненциального тренда, а также выведем на график уравнение тренда и параметр r 2 (рис. 12).
Рис. 12. График экспоненциального тренда для предсказания реальных доходов компании Wm. Wrigley Jr.
Экспоненциальная модель аппроксимирует временной ряд почти так же, как линейная и квадратичная модель. Скорректированный коэффициент r 2 равен 0,960, в то время как для линейной модели этот коэффициент равен 0,966, а для квадратичной – 0,965.
Выбор модели на основе разностей первого и второго порядка, а также относительных разностей
Для аппроксимации данных о реальном доходе компании Wm. Wrigley Jr. Company мы применили три модели: линейную, квадратичную и экспоненциальную. Какая из этих моделей лучше? Кроме визуального впечатления и сравнения скорректированных коэффициентов r 2 , в качестве инструмента для оценки качества модели применяются разности первого, второго и третьего порядка.
Выбор модели на основе анализа разностей первого и второго порядка, а также относительных разностей:
Не следует ожидать, что модель будет идеально аппроксимировать конкретный набор данных. Несмотря на это, при выборе подходящей модели необходимо анализировать разности первого и второго порядка, а также относительные разности. Для нашего примера с компанией Wm. Wrigley Jr. результаты такого анализа приведены на рис. 13.
Рис. 13. Разности первого и второго порядка, а также относительные разности, вычисленные на основе данных о реальных доходах компании Wm. Wrigley Jr.
Анализ рис. 13 показывает, что разности первого и второго порядка, а также относительные разности не остаются постоянными. Итак, несмотря на то, что скорректированный коэффициент r 2 у всех трех моделей, рассмотренных выше, одинаков и приближенно равен 0,96, возможно, существуют более точные модели.
Вычисление тренда с помощью авторегрессии и прогнозирование
Другой подход к прогнозированию основан на авторегрессионной модели. Часто значения временного ряда в какой-то момент времени сильно коррелируют как с предшествующими, так и с последующими значениями. Автокорреляция первого порядка оценивает степень зависимости между последовательными значениями временного ряда. Автокорреляция второго порядка оценивает силу связи между значениями, разделенными двумя временными интервалами. Автокорреляция р-го порядка представляет собой величину корреляции между значениями, разделенными р временными интервалами. Авторегрессионная модель позволяет лучше оценить предысторию и получить более точный прогноз.
Авторегрессионная модель первого порядка внешне напоминает модель простой линейной регрессии, а авторегрессионные модели второго и р-го порядков похожи на модель множественной регрессии. В регрессионных моделях параметры регрессии обозначаются символами β0, β1, …, βk а их оценки — символами b0, b1, …, bk. В авторегрессионных моделях аналогичные параметры обозначаются символами А0, А1 …, Аp, а их оценки — символами а0, а0, …, аp.
В авторегрессионной модели первого порядка рассматриваются лишь соседние значения временного ряда. В авторегрессионной модели второго порядка оценивается зависимость и корреляция как между соседними, так и между последовательными значениями временного ряда, разделенными двумя временными интервалами. В авторегрессионной модели р-го порядка оценивается зависимость и корреляция между соседними значениями, последовательными значениями временного ряда, разделенными двумя временными интервалами, и так далее вплоть до последовательных значений временного ряда, разделенных р временными интервалами.
Выбор подходящей авторегрессионной модели представляет собой нелегкую задачу. В процессе ее решения необходимо оценить простоту модели и возможные потери вследствие игнорирования автокорреляции между данными. С другой стороны, модели высоких порядков сопряжены с оценками многочисленных параметров, которые могут оказаться бесполезными, особенно если длина n временного ряда не очень велика. Это происходит потому, что при вычислении параметра Ар каждое значение временного ряда Yi сравнивается с его ближайшими соседями, расположенными не далее, чем через р временных интервалов (т.е. величина Yi сравнивается со значениями Yi–1, Yi–2, …, Yi–p). Иными словами, чем выше порядок авторегрессионной модели, тем больше первых ее членов теряется.
Выбрав модель и применив метод наименьших квадратов для вычисления оценок регрессионных параметров, необходимо оценить ее адекватность. Для этого можно использовать либо авторегрессионную модель конкретного порядка, которую уже применяли для похожих данных, либо сразу построить модель с несколькими параметрами, а затем последовательно исключать из нее параметры, не имеющие статистически значимого вклада. В последнем случае применяется t-критерий значимости параметра Аp, имеющего наивысший порядок в данной авторегрессионной модели. Нулевая и альтернативная гипотезы формулируются следующим образом: H0: Ар = 0, H1: Ар ≠ 0.
Использование t-критерия значимости параметра авторегрессии Ар, имеющего наивысший порядок:
где Аp — гипотетическое значение параметра, имеющего наивысший порядок в регрессионной модели, ар — оценка параметра авторегрессии Аp, имеющего наивысший порядок, Sap — стандартная ошибка оценки ар. Тестовая t-статистика имеет t-распределение с n–2р–1 степенями свободы. [2]
При заданном уровне значимости α нулевая гипотеза отклоняется, если тестовая t-статистика больше верхнего или меньше нижнего критического уровня t-распределения. Иначе говоря, решающее правило формулируется следующим образом: если t > tU или t α = 0,05, нулевую гипотезу Н0 отклонять нельзя. Таким образом, параметр третьего порядка не имеет статистической значимости в авторегрессионной модели и должен быть удален.
Повторим анализ для авторегрессионной модели второго порядка (рис. 17). Оценка параметра, имеющего наивысший порядок, а2 = –0,205, а ее стандартная ошибка равна 0,276. Для проверки гипотез Н0: А2 = 0 и Н1: А2 ≠ 0 вычислим t-статистику:
Рис. 17. Авторегрессионная модель второго порядка для реальных доходов компании Wm. Wrigley Jr.
При уровне значимости α = 0,05, критические величины двухстороннего t-критерия с n–2p–1 = 20–2*2–1 = 15 степенями свободы равны: tL =СТЬЮДЕНТ.ОБР(0,025;15) = –2,131; tU =СТЬЮДЕНТ.ОБР(0,975;15) = +2,131. Поскольку –2,131 α = 0,05, нулевую гипотезу Н0 отклонять нельзя. Таким образом, параметр второго порядка не является статистически значимым, и его следует удалить из модели.
Повторим анализ для авторегрессионной модели первого порядка (рис. 18). Оценка параметра, имеющего наивысший порядок, а1 = 1,024, а ее стандартная ошибка равна 0,039. Для проверки гипотез Н0: А1 = 0 и Н1: А1 ≠ 0 вычислим t-статистику:
Рис. 18. Авторегрессионная модель первого порядка для реальных доходов компании Wm. Wrigley Jr.
При уровне значимости α = 0,05, критические величины двухстороннего t-критерия с n–2p–1 = 20–2*1–1 = 17 степенями свободы равны: tL =СТЬЮДЕНТ.ОБР(0,025;17) = –2,110; tU =СТЬЮДЕНТ.ОБР(0,975;17) = +2,110. Поскольку –2,110 2 равен 99,4% (ячейки J5), скорректированный коэффициент смешанной корреляции — 99,3% (ячейки J6), тестовая F-статистика — 1 333,51 (ячейки M12), а р-значение равно 0,0000. При уровне значимости α = 0,05, каждый регрессионный коэффициент в классической мультипликативной модели временного ряда является статистически значимым. Применяя к ним операцию потенцирования, получаем следующие параметры:
Коэффициенты 
- Параметр
= 18 416,376, сдвиг зависимой переменной Y, является значением некорректированного тренда квартальных доходов в первом квартале 1994 года, т.е. в первом временном периоде.
- Величина (
— 1) х 100% = 3,66% оценивает темп роста квартальных доходов.
- Величина
= 0,807 представляет собой сезонный множитель для первого квартала по отношению к четвертому кварталу. Это число означает, что доходы, полученные в первом квартале, на 19,3% меньше, чем доходы, полученные в четвертом квартале.
- Величина
= 0,869 представляет собой сезонный множитель для второго квартала по отношению к четвертому. Это число означает, что доходы, полученные во втором квартале, на 13,1% меньше, чем доходы, полученные в четвертом квартале.
- Величина
= 0,848 представляет собой сезонный множитель для третьего квартала по отношению к четвертому. Это число означает, что доходы, полученные в третьем квартале, на 15,2% меньше, чем доходы, полученные в четвертом квартале.
Используя регрессионные коэффициенты bi, можно предсказать доход, полученный компанией в конкретном квартале. Например, предскажем доход компании для четвертого квартала 2002 года (Xi = 35):
log

Таким образом, согласно прогнозу в четвертом квартале 2002 года компания должна была получить доход, равный 67 млрд. долл. (вряд ли следует делать прогноз с точностью до миллиона). Для того чтобы распространить прогноз на период времени, находящийся за пределами временного ряда, например, на первый квартал 2003 года (Xi = 36, Q1 = 1), необходимо выполнить следующие вычисления:

Индексы
Индексы используются в качестве индикаторов, реагирующих на изменения экономической ситуации или деловой активности. Существуют многочисленные разновидности индексов, в частности, индексы цен, количественные индексы, ценностные индексы и социологические индексы. В данном разделе мы рассмотрим лишь индекс цен. Индекс — величина некоторого экономического показателя (или группы показателей) в конкретный момент времени, выраженный в процентах от его значения в базовый момент времени.
Индекс цен. Простой индекс цен отражает процентное изменение цены товара (или группы товаров) в течение заданного периода времени по сравнению с ценой этого товара (или группы товаров) в конкретный момент времени в прошлом. При вычислении индекса цен прежде всего следует выбрать базовый промежуток времени — интервал времени в прошлом, с которым будут производиться сравнения. При выборе базового промежутка времени для конкретного индекса периоды экономической стабильности являются более предпочтительными по сравнению с периодами экономического подъема или спада. Кроме того, базовый промежуток не должен быть слишком удаленным во времени, чтобы на результаты сравнения не слишком сильно влияли изменения технологии и привычек потребителей. Индекс цен вычисляется по формуле:
Индекс цен — процентное изменение цены товара (или группы товаров) в заданный период времени по отношению к цене товара в базовый момент времени. В качестве примера рассмотрим индекс цен на неэтилированный бензин в США в промежутке времени с 1980 по 2002 г. (рис. 24). Например:
Рис. 24. Цена галлона неэтилированного бензина и простой индекс цен в США с 1980 по 2002 г. (базовые годы — 1980 и 1995)
Итак, в 2002 г. цена неэтилированного бензина в США была на 4,8% больше, чем в 1980 г. Анализ рис. 24 показывает, что индекс цен в 1981 и 1982 гг. был больше индекса цен в 1980 г., а затем вплоть до 2000 года не превышал базового уровня. Поскольку в качестве базового периода выбран 1980 г., вероятно, имеет смысл выбрать более близкий год, например, 1995 г. Формула для пересчета индекса по отношению к новому базовому промежутку времени:
где Iновый — новый индекс цен, Iстарый — старый индекс цен, Iновая база – значение индекса цен в новом базовом году при расчете для старого базового года.
Предположим, что в качестве новой базы выбран 1995 год. Используя формулу (10), получаем новый индекс цен для 2002 года:
Итак, в 2002 г. неэтилированный бензин в США стоил на 13,9% больше, чем в 1995 г.
Невзвешенные составные индексы цен. Несмотря на то что индекс цен на любой отдельный товар представляет несомненный интерес, более важным является индекс цен на группу товаров, позволяющий оценить стоимость и уровень жизни большого количества потребителей. Невзвешенный составной индекс цен, определенный формулой (11), приписывает каждому отдельному виду товаров одинаковый вес. Составной индекс цен отражает процентное изменение цены группы товаров (часто называемой потребительской корзиной) в заданный период времени по отношению к цене этой группы товаров в базовый момент времени.
где t — период времени (0, 1, 2, …), i — номер товара (1, 2, …, n), n — количество товаров в рассматриваемой группе, 


На рис. 25 представлены средние цены на три вида фруктов за период с 1980 по 1999 гг. Для вычисления невзвешенного составного индекса цен в разные годы применяется формула (11), считая базовым 1980 год.
Итак, в 1999 г. суммарная цена фунта яблок, фунта бананов и фунта апельсинов на 59,4% превышала суммарную цену на эти фрукты в 1980 г.
Рис. 25. Цены (в долл.) на три вида фруктов и невзвешенный составной индекс цен
Невзвешенный составной индекс цен выражает изменения цен на всю группу товаров с течением времени. Несмотря на то что этот индекс легко вычислять, у него есть два явных недостатка. Во-первых, при вычислении этого индекса все виды товаров считаются одинаково важными, поэтому дорогие товары приобретают излишнее влияние на индекс. Во-вторых, не все товары потребляются одинаково интенсивно, поэтому изменения цен на мало потребляемые товары слишком сильно влияют на невзвешенный индекс.
Взвешенные составные индексы цен. Из-за недостатков невзвешенных индексов цен более предпочтительными являются взвешенные индексы цен, учитывающие различия цен и уровней потребления товаров, образующих потребительскую корзину. Существуют два типа взвешенных составных индексов цен. Индекс цен Лапейрэ, определенный формулой (12), использует уровни потребления в базовом году. Взвешенный составной индекс цен позволяет учесть уровни потребления товаров, образующих потребительскую корзину, присваивая каждому товару определенный вес.
где t — период времени (0, 1, 2, …), i — номер товара (1, 2, …, n), n — количество товаров в рассматриваемой группе, 

Вычисления индекса Лапейрэ показаны на рис. 26; в качестве базового используется 1980 год.
Рис. 26. Цены (в долл.), количество (потребление в фунтах на душу населения) трех видов фруктов и индекс Лапейрэ
Итак, индекс Лапейрэ в 1999 г. равен 154,2. Это свидетельствует от том, что в 1999 году эти три вида фруктов были на 54,2% дороже, чем в 1980 году. Обратите внимание на то, что этот индекс меньше невзвешенного индекса, равного 159,4, поскольку цены на апельсины — фрукты, потребляемые меньше остальных, — выросли больше, чем цена яблок и бананов. Иначе говоря, поскольку цены на фрукты, потребляемые наиболее интенсивно, выросли меньше, чем цены на апельсины, индекс Лапейрэ меньше невзвешенного составного индекса.
Индекс цен Пааше использует уровни потребления товара в текущем, а не базовом периоде времени. Следовательно, индекс Пааше более точно отражает полную стоимость потребления товаров в заданный момент времени. Однако этот индекс имеет два существенных недостатка. Во-первых, как правило, текущие уровни потребления трудно определить. По этой причине многие популярные индексы используют индекс Лапейрэ, а не индекс Пааше. Во-вторых, если цена некоторого конкретного товара, входящего в потребительскую корзину, резко возрастает, покупатели снижают уровень его потребления по необходимости, а не вследствие изменения вкусов. Индекс Пааше вычисляется по формуле:
где t — период времени (0, 1, 2, …), i — номер товара (1, 2, …, n), n — количество товаров в рассматриваемой группе, 

Вычисления индекса Пааше показаны на рис. 27; в качестве базового используется 1980 год.
Рис. 27. Цены (в долл.), количество (потребление в фунтах на душу населения) трех видов фруктов и индекс Пааше
Итак, индекс Пааше в 1999 г. равен 147,0. Это свидетельствует от том, что в 1999 году эти три вида фруктов были на 47,0% дороже, чем в 1980 году.
Некоторые популярные индексы цен. В бизнесе и экономике используется несколько индексов цен. Наиболее популярным является индекс потребительских цен (Consumer Index Price — CPI). Официально этот индекс называется CPI-U, чтобы подчеркнуть, что он вычисляется для городов (urban), хотя, как правило, его называют просто CPI. Этот индекс ежемесячно публикуется Бюро статистики труда (U. S. Bureau of Labor Statistics) в качестве основного инструмента для измерения стоимости жизни в США. Индекс потребительских цен является составным и взвешенным по методу Лапейрэ. При его вычислении используются цены 400 наиболее широко потребляемых продуктов, видов одежды, транспортных, медицинских и коммунальных услуг. В данный момент при вычислении этого индекса в качестве базового используется период 1982–1984 гг. (рис. 28). Важной функцией индекса CPI является его использование в качестве дефлятора. Индекс CPI используется для пересчета фактических цен в реальные путем умножения каждой цены на коэффициент 100/CPI. Расчеты показывают, что за последние 30 лет среднегодовые темпы инфляции в США составили 2,9%.
Рис. 28. Динамика Consumer Index Price; полные данные см. Excel-файл
Другим важным индексом цен, публикуемым Бюро статистики труда, является индекс цен производителей (Producer Price Index — PPI). Индекс PPI является взвешенным составным индексом, использующим метод Лапейрэ для оценки изменения цен товаров, продаваемых их производителями. Индекс PPI является лидирующим индикатором для индекса CPI. Иначе говоря, увеличение индекса PPI приводит к увеличению индекса CPI, и наоборот, уменьшение индекса PPI приводит к уменьшению индекса CPI. Финансовые индексы, такие как индекс Доу-Джонса для акций промышленных предприятий (Dow Jones Industrial Average — DJIA), S&P 500 и NASDAQ, используются для оценки изменения стоимости акций в США. Многие индексы позволяют оценить прибыльность международных фондовых рынков. К таким индексам относятся индекс Nikkei в Японии, Dax 30 в Германии и SSE Composite в Китае.
Ловушки, связанные с анализом временных рядов
Значение методологии, использующей информацию о прошлом и настоящем для того, чтобы прогнозировать будущее, более двухсот лет назад красноречиво описал государственный деятель Патрик Генри: «У меня есть лишь одна лампа, освещающая путь, — мой опыт. Только знание прошлого позволяет судить о будущем».
Анализ временных рядов основан на предположении, что факторы, влиявшие на деловую активность в прошлом и влияющие в настоящем, будут действовать и в будущем. Если это правда, анализ временных рядов представляет собой эффективное средство прогнозирования и управления. Однако критики классических методов, основанных на анализе временных рядов, утверждают, что эти методы слишком наивны и примитивны. Иначе говоря, математическая модель, учитывающая факторы, действовавшие в прошлом, не должна механически экстраполировать тренды в будущее без учета экспертных оценок, опыта деловой активности, изменения технологии, а также привычек и потребностей людей. Пытаясь исправить это положение, в последние годы специалисты по эконометрии разрабатывали сложные компьютерные модели экономической активности, учитывающие перечисленные выше факторы.
Тем не менее, методы анализа временных рядов представляют собой превосходный инструмент прогнозирования (как краткосрочного, так и долгосрочного), если они применяются правильно, в сочетании с другими методами прогнозирования, а также с учетом экспертных оценок и опыта.
Резюме. В заметке с помощью анализа временных рядов разработаны модели для прогнозирования доходов трех компаний: Wm. Wrigley Jr. Company, Cabot Corporation и Wal-Mart. Описаны компоненты временного ряда, а также несколько подходов к прогнозированию годовых временных рядов — метод скользящих средних, метод экспоненциального сглаживания, линейная, квадратичная и экспоненциальная модели, а также авторегрессионная модель. Рассмотрена регрессионная модель, содержащая фиктивные переменные, соответствующие сезонному компоненту. Показано применение метода наименьших квадратов для прогнозирования месячных и квартальных временных рядов (рис. 29).
Рис. 29. Структурная схема заметки
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 983–1074
[2] Тестовая t-статистика теряет р степеней свободы при оценке наклона и одну при оценке сдвига генеральной совокупности откликов. Еще р степеней свободы утрачиваются при сравнении значений временного ряда.
Видео:1 8 Статистические методы прогнозированияСкачать

Прогнозирование. Регрессионный анализ, его реализация и прогнозирование
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Сущность метода регрессионного анализа
Одним из методов, используемых для прогнозирования, является регрессионный анализ.
Регрессия – это статистический метод, который позволяет найти уравнение, наилучшим образом описывающее совокупность данных, заданных таблицей.
| X | X1 | X2 | … | Xi | … | Xn |
|---|---|---|---|---|---|---|
| Y | Y1 | Y2 | … | Yi | … | Yn |
На графике данные отображаются точками. Регрессия позволяет подобрать к этим точкам кривую у=f(x), которая вычисляется по методу наименьших квадратов и даёт максимальное приближение к табличным данным.
По полученному уравнению можно вычислить (сделать прогноз) значение функции у для любого значения х , как внутри интервала изменения х из таблицы(интерполяция), так и вне его (экстраполяция).
Линейная регрессия
Линейная регрессия дает возможность наилучшим образом провести прямую линию через точки одномерного массива данных (рис.13.1 а). Уравнение с одной независимой переменной, описывающее прямую линию, имеет вид:
где:x – независимая переменная;
y – зависимая переменная;
m – характеристика наклона прямой;
b – точка пересечения прямой с осью у.
Например, имея данные о реализации товаров за год с помощью линейной регрессии можно получить коэффициенты прямой (1) и, предполагая дальнейший линейный рост, получить прогноз реализации на следующий год.
Нелинейная регрессия
Нелинейная регрессия позволяет подбирать к табличным данным нелинейное уравнение (рис. 13.1 рис. 13.1, б.) – параболу, гиперболу и др. Excel реализует нелинейность в виде экспоненты, т.е. подбирает кривую вида:
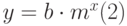
которая позволяет наилучшим образом провести экспоненциальную кривую по точкам данных, которые изменяются нелинейно.
Так, например, данные о росте населения почти всегда лучше описываются не прямой линией, а экспоненциальной кривой. При этом нужно помнить, что достоверное прогнозирование возможно только на участках подъёма или спуска кривой (при отрицательных значениях х), т.к. сама кривая (2) изменяется монотонно, без точек перегиба. Например, делать экспоненциальный прогноз для функции, изменяющейся синусоидально, можно только на участках подъёма или спуска функции, для чего её разбивают на соответствующие интервалы.
Множественная регрессия
Множественная регрессия представляет собой анализ более одного набора данных аргумента х и даёт более реалистичные результаты.
Множественный регрессионный анализ также может быть как линейным, так и экспоненциальным. Уравнение регрессии (1) и (2) примут соответственно вид (3) и (4):
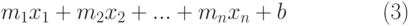 | ( 3) |
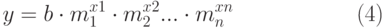 | ( 4) |
С помощью множественной регрессии, например, можно оценить стоимость дома в некотором районе, основываясь на данных его площади, размерах участка земли, этажности, вида из окон и т.д.
Использование функций регрессии
В Excel имеется 5 функций для линейной регрессии: ЛИНЕЙН(…)(LINEST), ТЕНДЕНЦИЯ(…), ПРЕДСКАЗ(…), НАКЛОН(…), СТОШУХ(…)) и 2 функции для экспоненциальной регрессии – ЛГРФПРИБЛ(…) и РОСТ(…).
Рассмотрим некоторые из них.
Функция ЛИНЕЙН((LINEST) вычисляет коэффициент m и постоянную b для уравнения прямой (1). Синтаксис функции:
Известные_значения_у и известные_значения_х – это множество значений у и необязательное множество значений х (их вводить необязательно), которые уже известны для соотношения (1).
Константа – это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
Статистика – это логическое значение, которое указывает требуется ли вывести дополнительную статистику по регрессии.
Если статистика имеет значение ЛОЖЬ (или 0), то функция ЛИНЕЙН возвращает только значения коэффициентов m и b , в противном случае выводится дополнительная регрессионная статистика в виде табл. 13.1 таблица 13.1:
| mn | mn-1 | … | m2 | m1 | b |
|---|---|---|---|---|---|
| sen | sen-1 | … | se2 | se1 | seb |
| r 2 | sey | … | #Н/Д | #Н/Д | #Н/Д |
| F | df | … | #Н/Д | #Н/Д | #Н/Д |
| ssreg | ssresid | … | #Н/Д | #Н/Д | #Н/Д |
где: se1 , se2,…,sen – стандартные значения ошибок для коэффициентов m1 , m2,…, mn ;
seb – стандартное значение ошибки для постоянной b (seb равно #Н/Д, т.е. «нет допустимого значения», если конст. имеет значение ЛОЖЬ);
r 2 – коэффициент детерминированности. Сравниваются фактические значения у и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями у. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений у;
sey – стандартная ошибка для оценки у (предельное отклонение для у);
F – F-cтатистика, или F-наблюдаемое значение. Она используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет;
df – степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надёжности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН;
ssreg – регрессионная сумма квадратов;
ssresid – остаточная сумма квадратов;
#Н/Д – ошибка, означающая «нет доступного значения».
Любую прямую можно задать её наклоном m и у-пересечением:
Наклон ( m ). Для того, чтобы определить наклон прямой, обычно обозначаемый через m , нужно взять 2 точки прямой (х1,у1) и (х2,у2); тогда наклон равен m=(y2-y1)/(x2-x1 ).
у-пересечение ( b ) прямой, обычно обозначаемое через b , является значение у для точки, в которой прямая пересекает ось у.
Уравнение прямой имеет вид: у=mx+b. Если известны значения m и b , то можно вычислить любую точку на прямой, подставляя значения у или х в уравнение. Можно также использовать функцию ТЕНДЕНЦИЯ ( TREND ) (см. ниже).
Если для функции у имеется только одна независимая переменная х, можно получить наклон и у-пересечение непосредственно, используя следующие формулы:
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точными являются модель, используемая функцией ЛИНЕЙН, и значения, получаемые из уравнения прямой.
В случае экспоненциальной регрессии аналогом функции (5) является функция ЛГРФПРИБЛ(LOGEST):
которая отличается лишь тем, что вычисляет коэффициенты m и b для экспоненциальной кривой (2).
Функция ТЕНДЕНЦИЯ(TREND) имеет вид:
возвращает числовые значения, лежащие на прямой линии, наилучшим образом аппроксимирующие известные табличные данные.
Новые_значения_х – это те, для которых необходимо вычислить соответствующие значения у.
Если параметр новые_значения_х пропущен, то считается, что он совпадает с известными х. Назначение остальных параметров функции ТЕНДЕНЦИЯ совпадает с описанными выше.
В случае экспоненциальной регрессии аналогом функции (7) является функция РОСТ(GROWTH):
возвращает стандартную погрешность регрессии – меру погрешности предсказываемого значения у для заданного значения х.
Правила ввода функций
Формулы(5)-(8) являются табличными, т.е. они заменяют собой несколько обычных формул и возвращают не один результат, а массив результатов. Поэтому необходимо соблюдать следующие правила:
- Перед вводом одной из формул (5)-(8) выведите блок ячеек, точно совпадающей по размеру с величиной возвращаемого формулой массива результатов. Например, при использовании функции ЛИНЕЙН с выводом статистики нужно выделить массив ячеек, равный табл. 13.1, если параметр статистики равен ЛОЖЬ, достаточно выделить одну строку табл. 13.1.
- Наберите функцию в строке формул. При этом слова на русском языке можно набирать строчными буквами, т.к. они являются ключевыми и при вводе Exсel автоматически переведет их в заглавные. Имена ячеек автоматически вводятся латинским шрифтом. Вместо слова ИСТИНА можно вводить числа от 1 до 9 (не 0), а вместо слова ЛОЖЬ – число 0. Если в результате, выполнения функции выводится одно число, можно вводить формулы не вручную, а использовать аппарат Мастера функций.
- Одновременно нажмите клавиши Shift+Ctrl+Enter . Результаты вычислений заполнят выделенные ячейки.
Линия тренда
Excel позволяет наглядно отображать тенденцию данных с помощью линии тренда, которая представляет собой интерполяционную кривую, описывающую отложенные на диаграмме данные.
Для того, чтобы дополнить диаграмму исходных данных линией тренда, необходимо выполнить следующие действия:
- выделить на диаграмме ряд данных, для которого требуется построить линию тренда;
- щелкнуть правой кнопкой мыши и выбрать команду Добавить линию тренда;
- в открывшемся окне задать метод интерполяции (линейный, полиномиальный, логарифмический и т. д.), а также через команду Параметры – другие параметры (например, вывод уравнения кривой тренда, коэффициента детерминированности r 2 , направление и количество периодов для экстраполяции (прогноза) и др.);
- нажать кнопку Закрыть.
Чтобы отобразить на графике (гистограмме и др.) новые, прогнозируемые в результате регрессионного анализа данные, нужно:
- определить их с помощью функции ТЕНДЕНЦИЯ, РОСТ или другим способом,
- выделить на диаграмме нужную кривую, щелкнув по ней правой кнопкой мыши,
- в появившемся окне выбрать команду Выбрать данные…, в появившемся окне выбрать диапазон ячеек с новыми данными вручную или протащив по ним курсор при нажатой левой клавише мыши, нажать ОК.
На диаграмме появится продолжение кривой, построенной по новым данным.
Простая линейная регрессия
Пример 1. Функция ТЕНДЕНЦИЯ(TREND)
а) Предположим, что фирма может приобрести земельный участок в июле. Фирма собирает информацию о ценах за последние 12 месяцев, начиная с марта, на типичный земельный участок. Название первого столбца «Месяц» с данными о номерах месяцев записано в ячейке А1, а второго столбца «Цена» – в ячейке В1. Номера месяцев с 1 по 12 (известные значения х) записаны в ячейки А2…А13. Известные значения у содержат множество известных значений (133 890 руб., 135 000 руб., 135 790 руб., 137 300 руб., 138 130 руб., 139 100 руб., 139 900 руб., 141 120 руб., 141 890 руб., 143 230 руб., 144 000 руб., 145 290 руб.), которые находятся в ячейках В2;В13 соответственно (данные условия). Новые значения х, т.е. числа 13, 14,15,16,17 введём в ячейки А14…А18. Для того чтобы определить ожидаемые значения цен на март, апрель, май, июнь, июль, выделим любой интервал ячеек, например, B14:B18 (по одной ячейке для каждого месяца) и в строке формул введем функцию:
После нажатия клавиш Ctrl+ Shift+Enter данная функция будет выделена как формула вертикального массива, а в ячейках B14:B18 появится результат: .
Таким образом, в июле фирма может ожидать цену около 150 244 руб.
б) Тот же результат будет получен, если вводить в формулу не все массивы переменных х и у, а использовать часть массивов, которые предусматриваются автоматически по умолчанию. Тогда формула (10) примет вид:
В формуле (11) используется массив по умолчанию (1:2:3:4:5:6:7:8:9:10:11:12) для аргумента «известные_значения_х», соответствующий 12 месяцам, для которых имеются данные по продажам. Он должен был бы быть помещен в формуле (11) между двумя знаками ;;. Массив (13:14:15:16:17) соответствует следующим 5 месяцам, для которых и получен массив результатов (146172:147190:148208:149226:150244).
Элементы массивов разделяет знак «:», который указывает на то, что они расположены по столбцам.
в) Аргумент «новые значения х» можно задать другим массивом ячеек, например, В14:В18, в которые предварительно записаны те же номера месяцев 13,14,15,16,17. Тогда вводимая в строку формул функция примет вид =ТЕНДЕНЦИЯ(В2:В13;;В14:В18).
Пример 2. Функция ЛИНЕЙН
а) Дана таблица изменения температуры в течение шести часов, введённая в ячейки D2 :E7 (табл. 13.2 таблица 13.2).
Требуется определить температуру во время восьмого часа.
| … | D | E |
|---|---|---|
| 1 | х-№часа | у-t о , град. |
| 2 | 1 | 2 |
| 3 | 2 | 3 |
| 4 | 3 | 4 |
| 5 | 4 | 7 |
| 6 | 5 | 12 |
| 7 | 6 | 18 |
Выделим ячейки D8:E12 для вывода результата, введем в строку ввода формулу =ЛИНЕЙН(Е2:Е7;D2:D7;1;1), нажмем клавиши Сtrl+Shift+Enter, в выделенных ячейках появится результат:
| 3,142857 | -3,3333333 |
| 0,540848 | 2,106302 |
| 0,894088 | 2,2625312 |
| 33,76744 | 4 |
| 172,8571 | 20,47619 |
Таким образом, коэффициент m=3,143 со стандартной ошибкой 0,541, а свободный член b=-3,333 со стандартной ошибкой 2,106, т.е. функция, описывающая данные табл. 13.2 таблица 13.2, имеет вид
Стандартные ошибки показывают максимально возможное отклонение параметра от рассчитанной величины. Для у оно составляет 2,263, т.е. реальное значение у может лежать в пределах 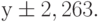
Точность приближения к табличным данным (коэффициент детерминированности r 2 ) составляет 0,894 или 89,4%, что является высоким показателем. При х=8 получим: у=3,143*8-3,333=21,81 град.
б) Тот же результат можно получить, использовав функцию =ТЕНДЕНЦИЯ(Е2:Е7;;G2:G5) для, например, следующих четырёх часов, предварительно введя в ячейки G2 :G5 числа с 7 до 10. Выделив ячейки Н2:Н5, введя в строку формул эту функцию и нажав Сtrl+Shift+Enter, получим в выделенных ячейках массив , т.е. для восьмого часа значение 
в) Функция ПРЕДСКАЗ ( FORECAST ) – позволяет предсказать значение у для нового значения х по известным значениям х и у, используя линейное приближение зависимости у=f(x).
Для данных примера 2 ввод формулы =ПРЕДСКАЗ(8;Е2:Е7;D2:D7) выводит в заранее выделенной ячейке результат 21,809. Новое значение х может быть задано не числом, а ячейкой, в которую записано это число.
Отличие функции ПРЕДСКАЗ от функции ТЕНДЕНЦИЯ заключается в том, что ПРЕДСКАЗ прогнозирует значения функции линейного приближения только для одного нового значения х.
Экспоненциальная регрессия
Пример 3
а) Функция ЛГРФПРИБЛ.
Рассмотрим условие примера 2.
Поскольку функция в табл. 13.2 таблица 13.2 носит явно нелинейный характер, целесообразно искать ее приближение в виде не прямой линии, как в примере 2, а в виде нелинейной кривой. Из всех видов нелинейности (гипербола, парабола, и др.) Excel реализует только экспоненциальное приближение вида у=b*mx c помощью функции ЛГРФПРИБЛ, которая рассчитывает для этого уравнения значения b и m .
Выделим для результата блок ячеек F8:G12 , введём в строку формул Функцию =ЛГРФПРИБЛ(Е2:Е7;D2:D7;1;1), нажмем клавиши Сtrl+Shift+Enter, в выделенных ячейках появится результат:
| 1,56628015 | 1,196513 |
| 0,02038299 | 0,07938 |
| 0,99181334 | 0,085268 |
| 484,599687 | 4 |
| 3,52335921 | 0,029083 |
Таким образом, коэффициент m=1,566, а b=1,197, т.е. уравнение приближающей кривой имеет вид:
со стандартными ошибками для m, b , и у равными 0,02, 0,079 и 0,085 соответственно. Коэффициент детерминированности r 2 =0,992, т.е. полученное уравнение даёт совпадение с табличными данными с вероятностью 99,2%.
Поскольку интерполяция табл. 13.2 таблица 13.2 экспоненциальной кривой даёт более точное приближение (99,2%) и с меньшими стандартными ошибками для m, b и у, в качестве приближающего уравнения принимаем уравнение (13).
При х=8 получим у=1,197*34,363=41,131 град.
б) Функция РОСТ вычисляет прогнозируемое по экспоненциальному приближению значение у для новых значений х, имеет формат:
Выделим блок ячеек F14: F17 , введём формулу =РОСТ(Е2:Е7;D2:D7;G2:G5;ИСТИНА), в выделенных ячейках появится массив чисел , т.е. при х=8 значение функции у=43,34 град. Это значение немного отличается от вычисленного в п. а), поскольку функция РОСТ использует для расчетов линию экспонециального тренда.
Примечание. При выборе экспоненциальной приближающей кривой следует учитывать, что интерполировать ею можно только участки, где функция монотонно возрастает или убывает (при отрицательном аргументе х), т.е. функцию, имеющую точки перегиба (например, параболу, синусоиду, кривую рис. 2 – т. А и др.) следует разбить на участки монотонного изменения от одной точки перегиба до другой и каждый участок интерполировать отдельно. Для рисунка 2 функцию нужно разбить на 2 участка – от начала до т. А и от т. А до конца кривой.
Множественная линейная регрессия
Пример 4
Предположим, что коммерческий агент рассматривает возможность закупки небольших зданий под офисы в традиционном деловом районе. Агент может использовать множественный регрессионный анализ для оценки цены здания под офис на основе следующих переменных:
у – оценочная цена здания под офис;
х1 – общая площадь в квадратных метрах;
х2 – количество офисов;
х3 – количество входов;
х4 – время эксплуатации здания в годах.
Агент наугад выбирает 11 зданий из имеющихся 1500 и получает следующие данные:
| А | В | С | D | Е | |
|---|---|---|---|---|---|
| 1 | х1— площадь, м2 | х2 – офисы | х3 – входы | х4 – срок, лет | у – цена, у.е. |
| 2 | 2310 | 2 | 2 | 20 | 42000 |
| 3 | 2333 | 2 | 2 | 12 | 144000 |
| 4 | 2356 | 3 | 1,5 | 33 | 151000 |
| 5 | 2379 | 3 | 2 | 43 | 151000 |
| 6 | 2402 | 2 | 3 | 53 | 139000 |
| 7 | 2425 | 4 | 3 | 23 | 169000 |
| 8 | 2448 | 2 | 1,5 | 99 | 126000 |
| 9 | 2471 | 2 | 2 | 34 | 142000 |
| 10 | 2494 | 3 | 3 | 23 | 163000 |
| 11 | 2517 | 4 | 4 | 55 | 169000 |
| 12 | 2540 | 2 | 3 | 22 | 149000 |
«Пол-входа» означает вход только для доставки корреспонденции.
В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (х1,х2,х3,х4) и зависимой переменной (у), т.е. ценой зданий под офис в данном районе.
- выделим блок ячеек А14:Е18 (в соответствии с табл. 13.1 таблица 13.1),
- введём формулу =ЛИНЕЙН(Е2:Е12;А2:D12;ИСТИНА;ИСТИНА), —
- нажмём клавиши Ctrl+Shift+Enter ,
- в выделенных ячейках появится результат:
| А | В | С | D | E | |
|---|---|---|---|---|---|
| 14 | -234,237 | 2553,210 | 12529,7682 | 27,6413 | 52317,83 |
| 15 | 13,2680 | 530,6691 | 400,066838 | 5,42937 | 12237,36 |
| 16 | 0,99674 | 970,5784 | #Н/Д | #Н/Д | #Н/Д |
| 17 | 459,753 | 6 | #Н/Д | #Н/Д | #Н/Д |
| 18 | 1732393319 | 5652135 | #Н/Д | #Н/Д | #Н/Д |
Уравнение множественной регрессии 
Теперь агент может определить оценочную стоимость здания под офис в том же районе, которое имеет площадь 2500 м 2 , три офиса, два входа, зданию 25 лет, используя следующее уравнение:
Это значение может быть вычислено с помощью функции ТЕНДЕНЦИЯ:
При интерполяции с помощью функции
для получения уравнения множественной экспоненциальной регрессии выводится результат:
| 0,99835752 | 1,0173792 | 1,0830186 | 1,0001704 | 81510,335 |
| 0,00014837 | 0,0065041 | 0,0048724 | 6,033Е-05 | 0,1365601 |
| 0,99158875 | 0,0105158 | #Н/Д | #Н/Д | #Н/Д |
| 176,832548 | 6 | #Н/Д | #Н/Д | #Н/Д |
| 0,07821851 | 0,0006635 | #Н/Д | #Н/Д | #Н/Д |
| #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
Коэффициент детерминированности здесь составляет 0,992 (99,2%), т.е. меньше, чем при линейной интерполяции, поэтому в качестве основного следует оставить уравнение множественной регрессии (14).
Таким образом, функции ЛИНЕЙН, ЛГРФПРИБЛ, НАКЛОН определяют коэффициенты, свободные члены и статистические параметры для уравнений одномерной и множественной регрессии, а функции ТЕНДЕНЦИЯ, ПРЕДСКАЗ, РОСТ позволяют получить прогноз новых значений без составления уравнения регрессии по значениям тренда.
ЗАДАНИЕ
Вариант задания к данной лабораторной работе включает две задачи. Для каждой из них необходимо составить и определить:
- Таблицу исходных данных, а также значений, полученных методами линейной и экспоненциальной регрессии.
- Коэффициенты в уравнениях прямой и экспоненциальной кривой (функции ЛИНЕЙН и ЛГРФПРИБЛ), напишите уравнения прямой и экспоненциальной кривой для простой и множественной регрессии.
- Погрешности (ошибки) прямой и экспоненциальной кривой, вычислений для коэффициентов и функций, коэффициенты детерминированности. Оценить, какой тип регрессии наилучшим образом подходит для вашего варианта задания.
- Прогноз изменения данных, выполненный с использованием линейной и экспоненциальной регрессии (функции ТЕНДЕНЦИЯ, ПРЕДСКАЗ, РОСТ).
- Построить гистограмму (или график) исходных данных для задачи 1 (одномерная регрессия), отобразить на ней линию тренда, а также соответствующее ей уравнение и коэффициент детерминированности.
Варианты заданий (номер варианта соответствует номеру компьютера).
- На рынке наблюдается стойкое снижение цен на компьютеры. Сделать прогноз, на сколько необходимо будет снизить цену на компьютеры в следующем месяце в вашей фирме, чтобы как минимум сравнять её с ценой на аналогичные компьютеры в конкурирующей фирме, если известна динамика изменения цен на них в конкурирующей фирме за последние 12 месяцев.
Для выполнения задания нужно ввести ряд из 12 ячеек с ценами конкурирующей фирмы, сделать прогноз цены на следующий месяц и др. (см. Задание).
- Известна структура расходов фирмы на рекламу в газетах, на радио, в журналах, на телевидении, на наружную рекламу (в процентах от общей суммы), а также оборот фирмы в каждом за последние 6 месяцев. Какой оборот можно ожидать в следующем месяце, если предполагается следующая структура расходов на рекламу: газеты-40%, журналы-40%, радио-5%, телевидение-14%, наружная реклама-1%.
Для выполнения задания нужно составить таблицу со столбцами вида:
| Месяц | х1-газеты,% | х2-журн.,% | х3-рад.,% | х4-телев.,% | х5-нар. рекл.,% | Оборот, $ |
|---|---|---|---|---|---|---|
| 1 | 37 | 34 | 12 | 10 | 5 | 410000 |
| 2 | 38 | 37 | 10 | 11 | 6 | 411500 |
| 3 | 39 | 38 | 9 | 13 | 7 | 413700 |
| 4 | 40 | 39 | 8 | 15 | 8 | 417050 |
| 5 | 41 | 40 | 7 | 16 | 9 | 420000 |
| 6 | 42 | 42 | 5 | 17 | 10 | 425000 |
и сделать множественный регрессионный прогноз (см. Задание).
- Имеются данные об объеме продаж в расчете на душу населения по хлебу и молоку и данные по годовым доходам на душу за 10 лет. По каждому товару построить модели регрессии для объемов продаж и функции размера доходов. Сделать прогноз о продажах и доходах на следующий год.
Для выполнения задания нужно составить таблицу вида:
| Годы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| х1-хлеб, кг | 23,5 | 26,7 | 27,9 | 30,1 | 31,5 | 35,7 | 38,3 | 40,1 | 41,5 | 42,8 | |
| х2-молоко, л | 20,45 | 22 | 23,8 | 25,9 | 27,4 | 29 | 33,5 | 36,8 | 38,1 | 39,5 | |
| У-доход, р. | 6600 | 7200 | 8400 | 10500 | 12750 | 14730 | 16240 | 17000 | 18050 | 18250 |
и получить два уравнения – у=f(x1) и у=f(x2), сделать прогноз на следующий год для рядов х1, х2, у и др. (см. Задание).
- Руководство фирмы провело оценку качеств пяти рекламных агентов по следующим признакам: х1 – эрудиция, х2 – знание предметной области. Полученные средние оценки, нормированные от 0 до 1, были сопоставлены с оценками эффективности деятельности агентов (% успешных сделок от количества возможных). Определить эффективность для агента с усреднёнными качествами. Сравнить её со средней эффективностью упомянутых 5 агентов.
Исходные данные нужно ввести в таблицу вида:
| А | В | С | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | х1-эрудиция | х2-энергичность | х3-люди | х4-внешность | х5-знания | Эффективность | |
| 2 | Агент 1 | 0,8 | 0,2 | 0,4 | 0,6 | 1,0 | 76% |
| 3 | Агент 2 | 0,74 | 0,3 | 0,39 | 0,58 | 0,95 | 78% |
| 4 | Агент 3 | 0,67 | 0,41 | 0,35 | 0,5 | 0,83 | 79% |
| 5 | Агент 6 | 0,59 | 0,59 | 0,33 | 0,47 | 0,8 | 80% |
| 6 | Агент 5 | 0,5 | 0,7 | 0,3 | 0,4 | 0,74 | 81% |
| 7 | Средняя эффективность пяти агентов | ||||||
| 8 | Средний агент | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | |
Массив ячеек В2-F6 заполняется произвольными числами от 0 до 1, столбец G2 -G6 – процентами удачных сделок по принципу «Чем выше уровень качеств агента, тем выше эффективность его работы», в ячейке G7 должна быть формула для вычисления среднего значения ячеек G2:G6 , в ячейке G8 нужно вычислить значение эффективности для среднего агента по формуле, полученной в результате множественного регрессионного анализа работы пяти агентов. Остальные пункты – см. Задание.
- Автосалон имеет данные о количестве проданных автомобилей «Мерседес» и «БМВ» за последние 4 квартала. Учитывая тенденцию изменения объёма продаж, определить, каких автомобилей нужно закупить больше («Мерседес» или «БМВ») в следующем квартале?
Для выполнения задания нужно составить и заполнить таблицу вида:
| Х | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Мерседес ( Y1 ) | 10 | 12 | 15 | 18 | |
| БМВ ( Y2 ) | 9 | 10 | 14 | 17 |
сделать прогноз продаж на новый квартал и выполнить другие пункты задания.
- Известны следующие данные о 5 недавно проданных подержанных автомобилях: у – стоимость продажи, х1 – стоимость аналогичного нового автомобиля, х2 – год выпуска, х3 – пробег, х4 – количество капитальных ремонтов, х5 – экспертные заключения о состоянии кузова и техническом состоянии автомобилей (по 10-бальной шкале). Определить, сколько может стоить автомобиль с соответствующими характеристиками: 340 000, 1998г., 140000км., 1, 6 (см. пример 4).
- Определить минимально необходимый тираж журнала и возможный доход от размещения в нём рекламы в следующем месяце, если известны данные об объёмах продаж этого журнала и доходах от размещения рекламы за последние 12 месяцев (считать, что расценки на рекламу не менялись).
Для выполнения задания нужно составить таблицу вида:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тираж,тыс. | 100 | 120 | 121,7 | 124,2 | 128 | 130,1 | 133,45 | 136 | 141 | 142,1 | 143,8 | 145 |
| Доход,тыс. руб. | 128 | 135 | 138 | 142 | 147 | 154 | 159 | 161 | 163 | 168 | 170,5 | 172 |
и заполнить ячейки за 12 месяцев условными данными. По этим данным нужно сделать линейный и экспоненциальный прогноз и др. (см. Задание).
- В целях привлечения покупателей и увеличения оборота фирма проводит стратегию ежемесячного снижения цен на свой товар. На основании данных о динамике изменения цен, объемов продаж в данной фирме и ещё в 3 конкурирующих фирмах за последние 12 месяцев сделать прогноз о том, возрастает ли объём продаж у данной фирмы при очередном снижении цен в следующем месяце, если предположить, что цены и объёмы у конкурентов в следующем месяце будут средние за рассматриваемый период.
Для выполнения задания нужно составить таблицу вида:
| Мес. | Фирма | Конкурент 1 | Конкурент 2 | Конкурент 3 | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | У-объём | х1-цена | х2-объём | х3-цена | х4-объём | х5-цена | х6-объём | х7-цена |
| 2 | 10000 | 1875 | 12000 | 1720 | 12500 | 1740 | 11970 | 1700 |
| 3 | 11000 | 1850 | 12340 | 1705 | 12620 | 1735 | 12100 | 1690 |
| 4 | 11570 | 1810 | 12750 | 1675 | 12740 | 1710 | 12350 | 1645 |
| 5 | 11850 | 1750 | 12910 | 1630 | 12960 | 1695 | 12500 | 1615 |
| 6 | 12100 | 1685 | 13100 | 1615 | 13000 | 1674 | 12630 | 1580 |
| 7 | 12340 | 1630 | 13570 | 1600 | 13210 | 1625 | 12920 | 1545 |
| 8 | 12750 | 1615 | 13820 | 1575 | 13320 | 1610 | 13150 | 1520 |
| 9 | 12910 | 1600 | 13980 | 1515 | 13460 | 1560 | 13300 | 1500 |
| 10 | 13100 | 1575 | 14000 | 1500 | 13600 | 1525 | 13610 | 1490 |
| 11 | 13230 | 1530 | 14070 | 1495 | 13780 | 1500 | 13850 | 1485 |
| 12 | 13470 | 1510 | 14120 | 1488 | 13900 | 1460 | 14000 | 1475 |
| 13 | ||||||||
- На основании данных о курсе американского доллара и немецкой марки в первом полугодии сделать прогноз о соотношении данных валют на второе полугодие. Во что будет выгоднее вкладывать деньги в конце года?
Для выполнения задания нужно составить таблицу вида:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Доллар | 24,5 | 24,9 | 25,7 | 26,9 | 28,0 | 28,8 | 29,3 | 29,7 | 30,5 | 30,9 | 31,8 | |
| Марка | 72,1 | 76,3 | 79,6 | 85,3 | 89,7 | 90,9 | 93,2 | 96,4 | 100,2 | 101,6 | 104,9 |
и сделать линейный прогноз на следующие 6 месяцев и др. (см. Задание).
- Известны данные за последние 6 месяцев о том, сколько раз выходила реклама фирмы, занимающейся недвижимостью, на телевидении – х1, радио – х2, в газетах и журналах – х3, а также количество звонков –у1 и количество совершённых сделок – у2. Какое соотношение количества совершённых сделок к количеству звонков у (в %) можно ожидать в следующем месяце, если известно, сколько раз выйдет реклама в каждом из перечисленных средств массовой информации.
Для выполнения задания нужно составить и заполнить таблицу вида:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | месяц | х1 | х2 | х3 | y=у2/у1*100% |
| 2 | 1 | 15 | 10 | 24 | 78% |
| 3 | 2 | 16 | 11 | 23 | 80% |
| 4 | 3 | 18 | 12 | 22 | 81% |
| 5 | 4 | 19 | 12 | 22 | 84% |
| 6 | 5 | 21 | 13 | 21 | 85% |
| 7 | 6 | 22 | 14 | 20 | 89% |
| 8 | 7 |
и выполнить применительно к таблице пункты Задания.
- Для некоторого региона известен среднегодовой доход населения, а также данные о структуре расходов (тыс. руб. в год) за последние 5 лет по следующим статьям: питание – х1, жильё – х2, одежда – х3, здоровье – х4, транспорт – х5, отдых – х6, образование – х7. На основании известных данных провести анализ потребительского кредита (или накопления) в следующем 6 году.
Для выполнения задания нужно составить и заполнить таблицу вида
| Годы | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Расход 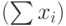 | Доход | Кредит(Y) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 2 | 1,3 | 1 | 0,3 | 5 | 4 | 18,6 | 21,4 | 3,1 |
| 2 | 5,2 | 2,2 | 1,2 | 1,2 | 0,4 | 4,8 | 4,5 | 19,5 | 22 | 2,5 |
| 3 | 5,5 | 2,5 | 1,1 | 1,4 | 0,6 | 4,6 | 4,9 | 20,6 | 23,4 | 2,8 |
| 4 | 5,8 | 2,7 | 0,9 | 1,6 | 1 | 4,2 | 5,6 | 21,8 | 25,8 | 4 |
| 5 | 7 | 3 | 0,8 | 2 | 1,2 | 4 | 6,5 | 24,7 | 26,2 | 1,5 |
| 6 | 7,5 | 3,3 | 0,7 | 2,2 | 1,5 | 3,8 | 7 | 26,5 | 27,5 |
В ячейках столбца 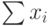
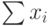
- Для 10 однокомнатных квартир, расположенных в одном районе, известны следующие данные: общая площадь – х1, жилая площадь – х2, площадь кухни – х3, наличие балкона – х4, телефона – х5, этаж – х6, а также стоимость – y . Определить, сколько может стоить однокомнатная квартира в этом районе без балкона, без телефона, расположенная на 1-ом этаже, общей площадью 28 м 2 , жилой – 16 м 2 , с кухней 6 м 2 .
| Квартиры | X1 | X2 | X3 | X4 | X5 | Стоимость ( y ) |
|---|---|---|---|---|---|---|
| 1 | 41 | 33 | 7 | 1 | 2 | 42000 |
| 2 | 40 | 30 | 7,7 | 2 | 3 | 40000 |
| 3 | 45 | 37 | 8 | 0 | 5 | 47000 |
| 4 | 46,3 | 34 | 9 | 1 | 6 | 49500 |
| 5 | 50 | 36 | 9 | 1 | 4 | 51000 |
| 6 | 53 | 40 | 9,5 | 1 | 7 | 55000 |
| 7 | 56 | 41 | 10 | 0 | 9 | 62000 |
| 8 | 60 | 47 | 12 | 2 | 10 | 62300 |
| 9 | 65 | 49 | 14 | 2 | 12 | 69000 |
| 10 | 70 | 58 | 14,5 | 2 | 14 | 72000 |
| 11 | 28 | 16 | 6 | 0 | 1 |
- Определить возможный прирост населения (кол-во человек на 1000 населения) в 2011 году, если известны данные о кол-ве родившихся и умерших на 1000 населения в 1997-2006 годах.
| Годы | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2011 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Родились | 100 | 110 | 130 | 155 | 170 | 174 | 180 | 185 | 190 | 200 | |
| Умерли | 108 | 115 | 135 | 160 | 178 | 180 | 186 | 190 | 197 | 205 |
- После некоторого спада наметился рост объёмов продаж матричных принтеров. Используя данные об объёмах продаж, ценах на матричные, струйные и лазерные принтеры, а также на их расходные материалы за последние 6 месяцев, определить возможный спрос на матричные принтеры в следующем месяце.
Проанализируйте, связано ли увеличение спроса на матричные принтеры с уменьшением спроса на струйные и лазерные.
| Матричные принтеры | Струйные принтеры | Лазерные принтеры | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Спрос у1 | Цена х1 | Рас.мат. z1 | Спрос у2 | Цена х2 | Рас.мат. z/2 | Спрос у3 | Цена х3 | Рас.мат. z3 | |
| 1 | 56 | 4172 | 174 | 26 | 2384 | 558 | 13 | 12517 | 1558 |
| 2 | 58 | 4250 | 179 | 24 | 2398 | 570 | 11 | 12984 | 1612 |
| 3 | 60 | 4289 | 182 | 23 | 2401 | 598 | 9 | 13259 | 1789 |
| 4 | 65 | 4297 | 194 | 20 | 2456 | 649 | 8 | 13687 | 1865 |
| 5 | 69 | 4305 | 205 | 19 | 2512 | 722 | 7 | 14013 | 1998 |
| 6 | 75 | 4318 | 213 | 18 | 2543 | 768 | 6 | 14587 | 2200 |
| 7 | 4456 | 220 | 17 | 2601 | 779 | 5 | 14789 | 2245 | |
Необходимо сделать прогноз на седьмой месяц по уравнению у1=f(x1,z1), получить уравнение y=(у2,x2, z2, у3, x3, z2 ) и проанализировать его. Если слагаемые у2 и у3 входят в регрессионное уравнение со знаком «-«, то уменьшение спросов у2 и у3 ведёт к увеличению спроса у1.
- Построить прогноз развития спроса населения на телевизоры, если известна динамика продаж телевизоров (тыс. шт.) и динамика численности населения (тыс. чел.) за 10 лет. По данным таблицы сделать прогноз по обоим рядам на следующий год. Выполнить другие пункты задания.
| Годы | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Динамика населения (тыс. чел) | 21,5 | 26,1 | 31,5 | 34,9 | 45,1 | 50,8 | 56 | 59,4 | 63,9 | 67,1 | |
| Динамика продаж (тыс. шт.) | 2,5 | 2,9 | 3,4 | 3,9 | 4,1 | 4,8 | 5 | 5,6 | 5,9 | 6,2 |
- Размещая рекламу в 4-х изданиях, фирма собрала сведения о поступивших на нее откликов – у и сопоставила их с данными об изданиях: х1 – стоимость издания, х2 – стоимость одного блока рекламы, х3 – тираж, х4 – объём аудитории, х5 – периодичность, х6 – наличие телепрограммы. Какое количество откликов можно ожидать на рекламу в издании со следующими характеристиками: 15000 руб., 10$, 1000 экз., 25000 чел., 4 раза в месяц, без телепрограммы.
Пользуясь данными таблицы
| Издания | х1 | х2 | х3 | х4 | х5 | х6 | Отклики, у |
|---|---|---|---|---|---|---|---|
| 1 | 10000 | 13 | 700 | 15000 | 4 | 1 | 108 |
| 2 | 12500 | 12 | 850 | 22000 | 8 | 1 | 115 |
| 3 | 15890 | 11,8 | 960 | 28000 | 10 | 0 | 120 |
| 4 | 17850 | 11 | 1200 | 32000 | 26 | 1 | 128 |
| 5 | 15000 | 10 | 1000 | 25000 | 4 | 0 |
необходимо сделать прогноз при заданных характеристиках.
- Размещая свою рекламу в 2-х печатных изданиях одновременно, фирма собрала сведения о количестве поступивших звонков и количестве заключенных сделок по объявлениям в каждом из указанных изданий за последние 12 месяцев. Определить, в каком из изданий и насколько эффективность размещения рекламы в следующем месяце будет больше?
| Месяцы | Издание 1 | Издание 2 | ||
|---|---|---|---|---|
| Звонки | Сделки | Звонки | Сделки | |
| 1 | 98 | 66 | 112 | 79 |
| 2 | 105 | 72 | 143 | 85 |
| 3 | 105 | 75 | 150 | 90 |
| 4 | 110 | 80 | 130 | 100 |
| 5 | 125 | 90 | 120 | 75 |
| 6 | 140 | 100 | 115 | 80 |
| 7 | 136 | 95 | 128 | 82 |
| 8 | 137 | 87 | 132 | 78 |
| 9 | 145 | 102 | 138 | 88 |
| 10 | 123 | 75 | 143 | 92 |
| 11 | 130 | 79 | 150 | 97 |
| 12 | 139 | 88 | 155 | 97 |
| 13 | ||||
Эффективность определяется как сделки/звонки. Сделать линейный и экспоненциальный прогнозы по обоим изданиям.
- Пусть комплект мягкой мебели (диван + 2 кресла) характеризуется стоимостью комплектующих: х1— деревянные подлокотники, х2 – велюровое покрытие, х3 – кресло-кровать, х4 – угловой диван, х5 – раскладывающийся диван, х6 – место для хранения белья. По данным о стоимости 5 комплектов сделать вывод о возможной стоимости комплекта с обычным раскладывающимся диваном, с местом для белья, без деревянных подлокотников и велюрового покрытия, с креслом кроватью.
Пользуясь данными таблицы
| Признаки | х1 | х2 | х3 | х4 | х5 | х6 | У -стоимость |
|---|---|---|---|---|---|---|---|
| Комплект 1 | 250 | 540 | 2500 | 4300 | 6400 | 800 | 13850 руб. |
| Комплект 2 | 320 | 650 | 3000 | 4800 | 7000 | 980 | 15770 руб. |
| Комплект 3 | 400 | 730 | 3900 | 6000 | 8500 | 1100 | 16730 руб. |
| Комплект 4 | 452 | 1300 | 4300 | 7500 | 9200 | 2050 | 24350 руб. |
| Комплект 5 | 550 | 1750 | 6400 | 12450 | 16700 | 4300 | 42150 руб. |
| Комплект 6 | 670 | 800 | 2750 | 6700 | 8800 | 1000 |
сделать прогноз и выполнить другие пункты задания.
- Для 2-х радиостанций известны данные об изменении объёма аудитории и динамике роста цен за 1 минуту эфирного времени за последние 12 месяцев. Определить, для какой радиостанции стоимость одного контакта со слушателем будет меньше?
| Месяц | Радиостанция 1 | Радиостанция 2 | ||
|---|---|---|---|---|
| Аудитория | Цена 1 мин. | Аудитория | Цена 1 мин. | |
| 1 | 250000 | 8000 | 300000 | 7560 |
| 2 | 540000 | 6500 | 450000 | 6340 |
| 3 | 580000 | 6460 | 490000 | 6250 |
| 4 | 650000 | 6300 | 550000 | 6000 |
| 5 | 730000 | 6060 | 610000 | 5730 |
| 6 | 750000 | 6000 | 690000 | 5300 |
| 7 | 800000 | 5400 | 750000 | 5100 |
| 8 | 840000 | 5320 | 780000 | 5000 |
| 9 | 890000 | 5130 | 870000 | 4700 |
| 10 | 950000 | 5000 | 900000 | 4650 |
| 11 | 1000000 | 4800 | 940000 | 4600 |
| 12 | 1108000 | 4700 | 1025000 | 4540 |
| 13 | ||||
| Контакт | ||||
В строке «Контакт» в ячейках С8 и D8 должны быть записаны формулы = С7/В7 и =Е7/D7 соответственно, вычисляющие стоимость 1 мин. Эфира для одного слушателя в прогнозируемом месяце. Прогноз нужно выполнить для линейного и экспоненциального приближений и выбрать более достоверный, а также сделать другие пункты Задания.
- На основании данных ежемесячных исследований известна динамика рейтинга банка (в условных единицах) за последние 6 месяцев в следующих сферах:
- менеджмент и технология – х1;
- менеджеры и персонал – х2;
- культура банковского обслуживания – х3;
- имидж банка на рынке финансовых услуг – х4;
- реклама банка – х5.
Определить возможное изменение количества вкладчиков данного банка в следующем месяце, если известны значения сфер рейтинга и количество вкладчиков в каждом из рассматриваемых 6 месяцев.
🔥 Видео
Машинное обучение. Прогнозирование временных рядов. К.В. Воронцов, Школа анализа данных, Яндекс.Скачать

Временные ряды. Аддитивная и мультипликативная моделиСкачать

Занятие 20. Временные рядыСкачать

Простой метод долгосрочного прогнозирования многомерных временных рядовСкачать

Быстрое прогнозирование в Microsoft ExcelСкачать
Лекция 10 Прогнозирование временных рядовСкачать

14-11 Временные ряды в pythonСкачать

Лекция 9. Прогнозирование на основе регрессионной моделиСкачать

16. "Анализ и прогнозирование временных рядов", Иван ЮрченковСкачать

05 Стандартные метрики точности прогнозирования временных рядовСкачать

Прогнозирование в Excel с помощью линий трендаСкачать

6 ключевых методов предсказания временных рядов в одном коде: MA, LR, K_near , ARIMA, Prophet, LSTMСкачать

Регрессия в ExcelСкачать

«Временные ряды: почему прогнозирование — это сложно». Александр Кондофуров, AltexSoftСкачать

Множественная регрессияСкачать

Нейронные сети для предсказание временных рядов (Задача регрессии)Скачать

Кластеризация временных рядов: зачем, кому и как | Вебинар Станислава Гафарова | karpov.coursesСкачать











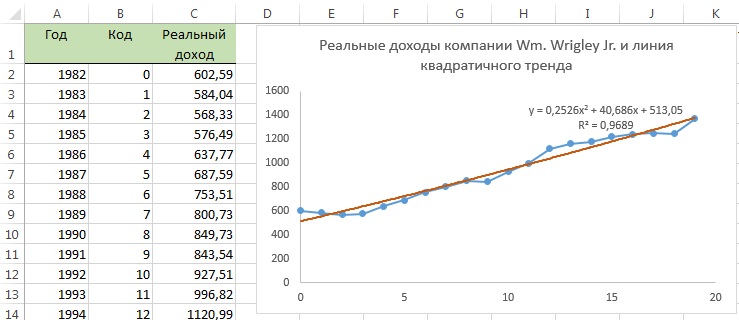










 = 18 416,376, сдвиг зависимой переменной Y, является значением некорректированного тренда квартальных доходов в первом квартале 1994 года, т.е. в первом временном периоде.
= 18 416,376, сдвиг зависимой переменной Y, является значением некорректированного тренда квартальных доходов в первом квартале 1994 года, т.е. в первом временном периоде. — 1) х 100% = 3,66% оценивает темп роста квартальных доходов.
— 1) х 100% = 3,66% оценивает темп роста квартальных доходов. = 0,807 представляет собой сезонный множитель для первого квартала по отношению к четвертому кварталу. Это число означает, что доходы, полученные в первом квартале, на 19,3% меньше, чем доходы, полученные в четвертом квартале.
= 0,807 представляет собой сезонный множитель для первого квартала по отношению к четвертому кварталу. Это число означает, что доходы, полученные в первом квартале, на 19,3% меньше, чем доходы, полученные в четвертом квартале. = 0,869 представляет собой сезонный множитель для второго квартала по отношению к четвертому. Это число означает, что доходы, полученные во втором квартале, на 13,1% меньше, чем доходы, полученные в четвертом квартале.
= 0,869 представляет собой сезонный множитель для второго квартала по отношению к четвертому. Это число означает, что доходы, полученные во втором квартале, на 13,1% меньше, чем доходы, полученные в четвертом квартале. = 0,848 представляет собой сезонный множитель для третьего квартала по отношению к четвертому. Это число означает, что доходы, полученные в третьем квартале, на 15,2% меньше, чем доходы, полученные в четвертом квартале.
= 0,848 представляет собой сезонный множитель для третьего квартала по отношению к четвертому. Это число означает, что доходы, полученные в третьем квартале, на 15,2% меньше, чем доходы, полученные в четвертом квартале.