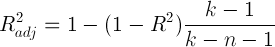Стандартная ошибка оценки по уравнению регрессии (5 видео)

Стандартная ошибка оценки по уравнению регрессии

Стандартная ошибка оценки, также известная как стандартная ошибка уравнения регрессии, определяется следующим образом (см. (6.23)) [c.280]

Стандартная ошибка уравнения регрессии, Эта статистика SEE представляет собой стандартное отклонение фактических значений теоретических значений У. [c.650]

Что такое стандартная ошибка уравнения регрессии ).Какие допущения лежат в основе парной регрессии 10. Что такое множественная регрессия [c.679]

Следующий этап корреляционного анализа — расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный показатель, потом второй, третий и т.д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, /»»-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей. Чем выше величина коэффициентов множественной корреляции, детерминации и критерия Фишера и чем ниже величина стандартной ошибки, тем точнее уравнение связи описывает зависимости, сложившиеся между исследуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то надо их отбросить, т.е. остановиться на том уравнении, где эти показатели наиболее оптимальны. [c.149]

Прогнозное значение ур определяется путем подстановки в уравнение регрессии ух =а + Ьх соответствующего (прогнозного) значения хр. Вычисляется средняя стандартная ошибка прогноза [c.9]

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка ть и та. [c.53]

В прогнозных расчетах по уравнению регрессии определяется предсказываемое (ур) значение как точечный прогноз ух при хр =хь т. е. путем подстановки в уравнение регрессии 5 = а + b х соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ух, т. е. Шух, и соответственно интервальной оценкой прогнозного значения (у ) [c.57]

Чтобы понять, как строится формула для определения величин стандартной ошибки ух, обратимся к уравнению линейной регрессии ух = а + b х. Подставим в это уравнение выражение параметра а [c.57]

При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора. [c.61]

В скобках указаны стандартные ошибки параметров уравнения регрессии. [c.327]

В скобках указаны стандартные ошибки параметров уравнения регрессии. Определим по этому уравнению расчетные значения >>, ,, а затем параметры уравнения регрессии (7.44). Получим следующие результаты [c.328]

На каждом шаге рассматриваются уравнение регрессии, коэффициенты корреляции и детерминации, F-критерий, стандартная ошибка оценки и другие оценочные показатели. После каждого шага перечисленные оценочные показатели сравниваются с [c.39]

Проблемы с методологией регрессии. Методология регрессии — это традиционный способ уплотнения больших массивов данных и их сведения в одно уравнение, отражающее связь между мультипликаторами РЕ и финансовыми фундаментальными переменными. Но данный подход имеет свои ограничения. Во-первых, независимые переменные коррелируют друг с другом . Например, как видно из таблицы 18,2, обобщающей корреляцию между коэффициентами бета, ростом и коэффициентами выплат для всех американских фирм, быстрорастущие фирмы обычно имеют большой риск и низкие коэффициенты выплат. Обратите внимание на отрицательную корреляцию между коэффициентами выплат и ростом, а также на положительную корреляцию между коэффициентами бета и ростом. Эта мультиколлинеарность делает мультипликаторы регрессии ненадежными (увеличивает стандартную ошибку) и, возможно, объясняет ошибочные знаки при коэффициентах и крупные изменения этих мультипликаторов в разные периоды. Во-вторых, регрессия основывается на линейной связи между мультипликаторами РЕ и фундаментальными переменными, и данное свойство, по всей вероятности, неадекватно. Анализ остаточных явлений, связанных с корреляцией, может привести к трансформациям независимых переменных (их квадратов или натуральных логарифмов), которые в большей степени подходят для объяснения мультипликаторов РЕ. В-третьих, базовая связь между мультипликаторами РЕ и финансовыми переменными сама по себе не является стабильной. Если же эта связь смещается из года в год, то прогнозы, полученные из регрессионного уравнения, могут оказаться ненадежными для более длительных периодов времени. По всем этим причинам, несмотря на полезность регрессионного анализа, его следует рассматривать только как еще один инструмент поиска подлинного значения ценности. [c.649]

На рисунке 16.6 явно просматривается четкая линейная зависимость объема частного потребления от величины располагаемого дохода. Уравнение парной линейной регрессии, оцененное по этим данным, имеет вид С= -217,6 + 1,007 Yf Стандартные ошибки для свободного члена и коэффициента парной регрессии равны, соответственно, 28,4 и 0,012, а -статистики — -7,7 и 81 9. Обе они по модулю существенно превышают 3, следовательно, их статистическая значимость весьма высока. Впрочем, несмотря на то, что здесь удалось оценить статистически значимую линейную функцию потребления, в ней нарушены сразу две предпосылки Кейнса — уровень автономного потребления С0 оказался отрицательным, а предель- [c.304]

Стандартные ошибки свободного члена и коэффициента регрессии равны, соответственно, 84,7 и 0,46 их /-статистики — (-21,4 и 36,8). По абсолютной величине /-статистики намного превышают 3, и это свидетельствует о высокой надежности оцененных коэффициентов. Коэффициент детерминации /Р уравнения равен 0,96, то есть объяснено 96% дисперсии объема потребления. И в то же время уже по рисунку видно, что оцененная рефессия не очень хоро- [c.320]

Эта стандартная ошибка S у, равная 0,65, указывает отклонение фактических данных от прогнозируемых на основании использования воздействующих факторов j i и Х2 (влияние среди покупателей бабушек с внучками и высокопрофессионального вклада Шарика). В то же время мы располагаем обычным стандартным отклонением Sn, равным 1,06 (см. табл.8), которое было рассчитано для одной переменной, а именно сами текущие значения уги величина среднего арифметического у, которое равно 6,01. Легко видеть, что S у tTa6n. В противном случае доверять полученной оценке параметра нет оснований. [c.139]

Для определения профиля посетителей магазинов местного торгового центра, не имеющих определенной цели (browsers), маркетологи использовали три набора независимых переменных демографические, покупательское поведение психологические. Зависимая переменная представляет собой индекс посещения магазина без определенной цели, индекс (browsing index). Методом ступенчатой включающей все три набора переменных, выявлено, что демографические факторы — наиболее сильные предикторы, определяющие поведение покупателей, не преследующих конкретных целей. Окончательное уравнение регрессии, 20 из 36 возможных переменных, включало все демографические переменные. В следующей таблице приведены коэффициенты регрессии, стандартные ошибки коэффициентов, а также их уровни значимости. [c.668]

Содержание

Смотреть страницы где упоминается термин Стандартная ошибка уравнения регрессии
Лекции по дисциплине «Эконометрика» (заочное отделение) (стр. 2 )
Оценка результатов линейной регрессии
Введение
Модель линейной регрессии
Функция summary.lm() и оценка получившихся результатов
Заключение
💡 Видео

Смотреть страницы где упоминается термин Стандартная ошибка уравнения регрессии

Маркетинговые исследования Издание 3 (2002) — [ c.650 ]

Видео:Эконометрика. Линейная парная регрессияСкачать

Лекции по дисциплине «Эконометрика» (заочное отделение) (стр. 2 )

Стандартная ошибка оценки по уравнению регрессии

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4

Параметр формально является значением Y при X = 0. Он может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре . Если > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация по фактору X выше вариации для результата Y. Также считают, что включает в себя неучтенные в модели факторы.

По итогам 2008 года были собраны данные по прибыли и оборачиваемости оборотных средств 500 торговых предприятий г. Челябинска. Результаты наблюдения сведены в таблицу.

Годовая прибыль предприятия, млн. руб.

Годовая оборачиваемость оборотных средств, раз

Требуется построить зависимость прибыли предприятий от оборачиваемости оборотных средств и оценить качество полученного уравнения.

Пусть y – прибыль предприятия, x – оборачиваемость оборотных средств.

На основе исходных данных были рассчитаны следующие показатели:

Уровень доверия возьмем q=0,95 или 95%.

1. Стандартные ошибки оценок , . намного больше =0,39, следовательно, низкая точность коэффициента . очень мала по сравнению с , следовательно, высокая точность коэффициента .

2. Интервальные оценки коэффициентов уравнения регрессии.

n – 2 = 500 – 2 = 498;

α: → → очень низкая точность коэффициента;

β: → → высокая точность коэффициента.

3. Значимость коэффициентов регрессии.

= >1,96 → коэффициент значим;

= >1,96 → коэффициент значим.

4. Стандартная ошибка регрессии. Se=0,91, по сравнению со средним значением =34,5 ошибка невысокая, точность уравнения хорошая.

5. Коэффициент детерминации. R2 = rxy2=0,782=0,6084 не очень близко к 1, качество подгонки среднее.

6. Средняя ошибка аппроксимации. A=11%, качество подгонки уравнения среднее.

Экономическая интерпретация: при увеличении оборачиваемости оборотных средств предприятия на 1 раз в год средняя годовая прибыль увеличится на 5,86 млн. руб.

Тема 6. Нелинейная парная регрессия

Часто на практике между зависимой и независимыми переменными существует нелинейная форма взаимосвязи. В этом случае существует два выхода:

1) подобрать к анализируемым переменным преобразование, которое бы позволило представить существующую зависимость в виде линейной функции;

2) применить нелинейный метод наименьших квадратов.

Основные нелинейные регрессионные модели и приведение их к линейной форме

1. Экспоненциальное уравнение .

Если прологарифмировать левую и правую части данного уравнения, то получится

Это уравнение является линейным, но вместо y в левой части стоит ln y.

В данном случае параметр β1 имеет следующий экономический смысл: при увеличении переменной x на единицу переменная y в среднем увеличится примерно на 100·β% (более точно: y увеличится в раз).

2. Логарифмическое уравнение .

Переход к линейному уравнению осуществляется заменой переменной x на X=lnx..

Параметр β1 имеет следующий экономический смысл: для увеличения y на единицу необходимо увеличить переменную x в раз, т. е. примерно на .

3. Гиперболическое уравнение .

В этом случае необходимо сделать замену переменных x на . Для гиперболической зависимости нет простой интерпретации коэффициента регрессии β1.

4. Степенное уравнение .

Прологарифмировав левую и правую части данного уравнения, получим

Заменив соответствующие ряды их логарифмами, получится линейная регрессия.

Экономический смысл параметра β1: если значение переменной x увеличить на 1%, то y увеличится на β1%.

5. Показательное уравнение (β1>0, β1≠1).

Прологарифмировав левую и правую части уравнения, получим

Проведя замены Y=ln y и B1=ln β1, получится линейная регрессия.

Экономический смысл параметра β1: при увеличении переменной x на единицу переменная y в среднем увеличится в β1 раз.

Тема 7. Множественная линейная регрессия: определение и оценка параметров

1. Понятие множественной линейной регрессии

Модель множественной линейной регрессии является обобщением парной линейной регрессии и представляет собой следующее выражение:

, t=1. n,

где yt – значение зависимой переменной для наблюдения t,

xit – значение i-й независимой переменной для наблюдения t,

εt – значение случайной ошибки для наблюдения t,

n – число наблюдений,

m – число независимых переменных x.

2. Матричная форма записи множественной линейной регрессии

Уравнение множественной линейной регрессии можно записать в матричной форме:

где , , , .

3. Основные предположения

2. для всех наблюдений;

3. = const для всех наблюдений;

4. ;

В случае выполнения вышеперечисленных гипотез модель называется нормальной линейной регрессионной.

4. Метод наименьших квадратов

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК): .

Чтобы найти минимум этой функции необходимо вычислить производные по каждому из параметров и приравнять их к нулю, в результате получается система уравнений, решение которой в матричном виде следующее:

→ .

5. Теорема Гаусса-Маркова

Если выполнены предположения 1-5 из пункта 3, то оценки , полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе линейных несмещенных оценок, то есть являются несмещенными, состоятельными и эффективными.

Тема 8. Множественная линейная регрессия: оценка качества

1. Общая схема проверки качества парной регрессии

Адекватность модели – остатки должны удовлетворять условиям теоремы Гаусса-Маркова.

Основные показатели качества коэффициентов регрессии:

1. Стандартные ошибки оценок (анализ точности определения оценок).

2. Интервальные оценки коэффициентов уравнения регрессии (построение доверительных интервалов).

3. Значимость коэффициентов регрессии (проверка гипотез относительно коэффициентов регрессии).

Основные показатели качества уравнения регрессии в целом:

1. Стандартная ошибка регрессии Se (анализ точности уравнения регрессии).

2. Значимость уравнения регрессии в целом (проверка гипотезы относительно всех коэффициентов регрессии).

3. Коэффициент детерминации R2 (проверка качества подгонки уравнения к исходным данным).

4. Скорректированный коэффициент детерминации R2adj (проверка качества подгонки уравнения к исходным данным).

5. Средняя ошибка аппроксимации (проверка качества подгонки уравнения к эмпирическим данным).

2. Стандартные ошибки оценок

Стандартные ошибки коэффициентов регрессии – это средние квадратические отклонения коэффициентов регрессии от их истинных значений.

где

— диагональные элементы матрицы ,

Стандартная ошибка является оценкой среднего квадратического отклонения коэффициента регрессии от его истинного значения. Чем меньше стандартная ошибка тем точнее оценка.

3. Интервальные оценки коэффициентов множественной линейной регрессии

Доверительные интервалы для коэффициентов регрессии определяются следующим образом:

1. Выбирается уровень доверия q (0,9; 0,95 или 0,99).

2. Рассчитывается уровень значимости g = 1 – q.

3. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

4. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.

5. Рассчитывается доверительный интервал для параметра :

Доверительный интервал показывает, что истинное значение параметра с вероятностью q находится в данных пределах.

Чем меньше доверительный интервал относительно коэффициента, тем точнее полученная оценка.

4. Значимость коэффициентов регрессии

Процедура оценки значимости коэффициентов осуществляется аналогичной парной регрессии следующим образом:

1. Рассчитывается значение t-статистики для коэффициента регрессии по формуле .

2. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).

3. Рассчитывается уровень значимости g = 1 – q.

4. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

5. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.

6. Если , то коэффициент является значимым на уровне значимости g. В противном случае коэффициент не значим (на данном уровне g).

t-тесты обеспечивают проверку значимости предельного вклада каждой переменной при допущении, что все остальные переменные уже включены в модель.

5. Стандартная ошибка регрессии

Стандартная ошибка регрессии Se показывает, насколько в среднем фактические значения зависимой переменной y отличаются от ее расчетных значений

Используется как основная величина для измерения качества модели (чем она меньше, тем лучше).

Значения Se в однотипных моделях с разным числом наблюдений и (или) переменных сравнимы.

6. Оценка значимости уравнения регрессии в целом

Уравнение значимо, если есть достаточно высокая вероятность того, что существует хотя бы один коэффициент, отличный от нуля.

Имеются альтернативные гипотезы:

Если принимается гипотеза H0, то уравнение статистически незначимо. В противном случае говорят, что уравнение статистически значимо.

Значимость уравнения регрессии в целом осуществляется с помощью F-статистики.

Оценка значимости уравнения регрессии в целом основана на тождестве дисперсионного анализа:

TSS – общая сумма квадратов отклонений

ESS – объясненная сумма квадратов отклонений

RSS – необъясненная сумма квадратов отклонений

F-статистика представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы)

n – число выборочных наблюдений, m – число независимых переменных.

При отсутствии линейной зависимости между зависимой и независимой переменными F-статистика имеет F-распределение Фишера-Снедекора со степенями свободы k1 = m, k2 = n – m –1.

Процедура оценки значимости уравнения осуществляется следующим образом:

7. Рассчитывается значение F-статистики по формуле .

8. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).

9. Рассчитывается уровень значимости g = 1 – q.

10. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

11. Определяется критическое значение F-статистики (Fкр) по таблицам распределения Фишера на основе g и n – m – 1.

12. Если , то уравнение является значимым на уровне значимости g. В противном случае уравнение не значимо (на данном уровне g).

В парной регрессии F-статистика равна квадрату t-статистики: , а значимость коэффициента регрессии и значимость уравнения в целом эквивалентны.

Качество оценки уравнения можно проверить путем расчета коэффициента детерминации R2, который показывает степень соответствия найденного уравнения экспериментальным данным.

Коэффициент R2 показывает долю дисперсии переменной y, объясненную регрессией, в общей дисперсии y.

Коэффициент детерминации лежит в пределах 0 £ R2 £ 1.

Чем ближе R2 к 1, тем выше качество подгонки уравнения к статистическим данным.

Чем ближе R2 к 0, тем ниже качество подгонки уравнения к статистическим данным.

Коэффициенты R2 в разных моделях с разным числом наблюдений и переменных несравнимы.

8. Скорректированный коэффициент детерминации R2adj

Низкое значение R2 не свидетельствует о плохом качестве модели, и может объясняться наличием существенных факторов, не включенных в модель

R2 всегда увеличивается с включением новой переменной. Поэтому его необходимо корректировать, и рассчитывают скорректированный коэффициент детерминации

Если R2adj выходит за пределы интервала [0;1], то его использовать нельзя.

Если при добавлении новой переменной в модель увеличивается не только R2, но и R2adj, то можно считать, что вклад этой переменной в повышение качества модели существенен.

9. Средняя ошибка аппроксимации

Средняя ошибка аппроксимации (средняя абсолютная процентная ошибка) – показывает в процентах среднее отклонение расчетных значений зависимой переменной от фактических значений yi

Если A ≤ 10%, то качество подгонки уравнения считается хорошим. Чем меньше значение A, тем лучше.

10. Использование показателей качества коэффициентов и уравнения регрессии для интерпретации и корректировки модели

В случае незначимости уравнения, необходимо устранить ошибки модели. Наиболее распространенными являются следующие ошибки:

— неправильно выбран вид функции регрессии;

— в модель включены незначимые регрессоры;

— в модели отсутствуют значимые регрессоры.

После устранения ошибок требуется заново оценить параметры уравнения и его качество, продолжая этот процесс до тех пор, пока качество уравнения не станет удовлетворительным. Если после поделанных процедур, мы не достигли требуемого уровня значимости, то необходимо устранять другие ошибки (спецификации, классификации, наблюдения и т. д., см. тему 3, п. 6).

11. Интерпретация множественной линейной регрессии

Коэффициент регрессии при переменной xi показывает, на сколько увеличится среднее значение зависимой переменной y при увеличении xi на 1, при условии постоянства других переменных.

В апреле 2006 года были собраны данные по стоимости 200 двухкомнатных квартир в Металлургическом районе г. Челябинска, их жилой площади, площади кухни и расстоянии до центра города (пл. Революции). Результаты наблюдения сведены в таблицу.

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Оценка результатов линейной регрессии

Введение

Модель линейной регрессии

Итак, пусть есть несколько независимых случайных величин X1, X2, . Xn (предикторов) и зависящая от них величина Y (предполагается, что все необходимые преобразования предикторов уже сделаны). Более того, мы предполагаем, что зависимость линейная, а ошибки рапределены нормально, то есть

где I — единичная квадратная матрица размера n x n.

Итак, у нас есть данные, состоящие из k наблюдений величин Y и Xi и мы хотим оценить коэффициенты. Стандартным методом для нахождения оценок коэффициентов является метод наименьших квадратов. И аналитическое решение, которое можно получить, применив этот метод, выглядит так: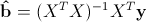

где b с крышкой — оценка вектора коэффициентов, y — вектор значений зависимой величины, а X — матрица размера k x n+1 (n — количество предикторов, k — количество наблюдений), у которой первый столбец состоит из единиц, второй — значения первого предиктора, третий — второго и так далее, а строки соответствуют имеющимся наблюдениям.

Функция summary.lm() и оценка получившихся результатов

Теперь рассмотрим пример построения модели линейной регрессии в языке R:

Таблица gala содержит некоторые данные о 30 Галапагосских островах. Мы будем рассматривать модель, где Species — количество разных видов растений на острове линейно зависит от нескольких других переменных.

Рассмотрим вывод функции summary.lm().
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков: минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, например тестом Шапиро-Уилка.
Далее — самое интересное — информация о коэффициентах. Здесь потребуется немного теории.
Сначала выпишем следующий результат:

при этом сигма в квадрате с крышкой является несмещенной оценкой для реальной сигмы в квадрате. Здесь b — реальный вектор коэффициентов, а эпсилон с крышкой — вектор остатков, если в качестве коэффициентов взять оценки, полученные методом наименьших квадратов. То есть при предположении, что ошибки распределены нормально, вектор коэффициентов тоже будет распределен нормально вокруг реального значения, а его дисперсию можно несмещенно оценить. Это значит, что можно проверять гипотезу на равенство коэффициентов нулю, а следовательно проверять значимость предикторов, то есть действительно ли величина Xi сильно влияет на качество построенной модели.
Для проверки этой гипотезы нам понадобится следующая статистика, имеющая распределение Стьюдента в том случае, если реальное значение коэффициента bi равно 0: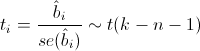

где
— стандартная ошибка оценки коэффициента, а t(k-n-1) — распределение Стьюдента с k-n-1 степенями свободы.

Теперь все готово для продолжения разбора вывода функции summary.lm().
Итак, далее идут оценки коэффициентов, полученные методом наименьших квадратов, их стандартные ошибки, значения t-статистики и p-значения для нее. Обычно p-значение сравнивается с каким-нибудь достаточно малым заранее выбранным порогом, например 0.05 или 0.01. И если значение p-статистики оказывается меньше порога, то гипотеза отвергается, если же больше, ничего конкретного, к сожалению, сказать нельзя. Напомню, что в данном случае, так как распределение Стьюдента симметричное относительно 0, то p-значение будет равно 1-F(|t|)+F(-|t|), где F — функция распределения Стьюдента с k-n-1 степенями свободы. Также, R любезно обозначает звездочками значимые коэффициенты, для которых p-значение достаточно мало. То есть, те коэффициенты, которые с очень малой вероятностью равны 0. В строке Signif. codes как раз содержится расшифровка звездочек: если их три, то p-значение от 0 до 0.001, если две, то оно от 0.001 до 0.01 и так далее. Если никаких значков нет, то р-значение больше 0.1.

В нашем примере можно с большой уверенностью сказать, что предикторы Elevation и Adjacent действительно с большой вероятностью влияют на величину Species, а вот про остальные предикторы ничего определенного сказать нельзя. Обычно, в таких случаях предикторы убирают по одному и смотрят, насколько изменяются другие показатели модели, например BIC или Adjusted R-squared, который будет разобран далее.

Значение Residual standart error соответствует просто оценке сигмы с крышкой, а степени свободы вычисляются как k-n-1.

А теперь самая важные статистики, на которые в первую очередь стоит смотреть: R-squared и Adjusted R-squared:

где Yi — реальные значения Y в каждом наблюдении, Yi с крышкой — значения, предсказанные моделью, Y с чертой — среднее по всем реальным значениям Yi.

Начнем со статистики R-квадрат или, как ее иногда называют, коэффициента детерминации. Она показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Если этот коэффициент близок к 1, то условная дисперсия модели достаточно мала и весьма вероятно, что модель неплохо описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей.

Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат. Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.

Для примера рассмотрим ту же модель, что и раньше, но теперь вместо пяти предикторов оставим два:

Как можно увидеть, значение статистики R-квадрат снизилось, однако значение скорректированного R-квадрат даже немного возросло.

Теперь проверим гипотезу о равенстве нулю всех коэффициентов при предикторах. То есть, гипотезу о том, зависит ли вообще величина Y от величин Xi линейно. Для этого можно использовать следующую статистику, которая, если гипотеза о равенстве нулю всех коэффициентов верна, имеет распределение Фишера c n и k-n-1 степенями свободы:

Значение F-статистики и p-значение для нее находятся в последней строке вывода функции summary.lm().

Заключение

В этой статье были описаны стандартные методы оценки значимости коэффициентов и некоторые критерии оценки качества построенной линейной модели. К сожалению, я не касался вопроса рассмотрения распределения остатков и проверки его на нормальность, поскольку это увеличило бы статью еще вдвое, хотя это и достаточно важный элемент проверки адекватности модели.
Очень надеюсь что мне удалось немного расширить стандартное представление о линейной регрессии, как об алгоритме который просто оценивает некоторый вид зависимости, и показать, как можно оценить его результаты.