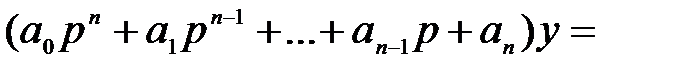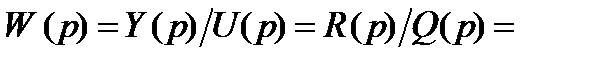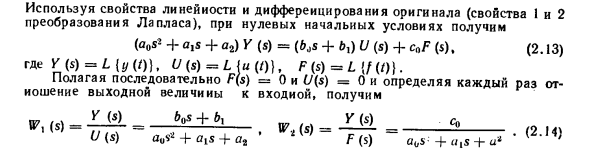

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Формы записи линейных дифференциальных уравнений. Передаточные функции
- Форма для написания линейных дифференциальных уравнений. Передаточная функция При описании автоматических систем управления магией широко используются символические формы, описывающие линейные дифференциальные уравнения. Рассмотрим пример из уравнения (2.5). Чтобы уменьшить нотацию, опустите символ A и перепишите его, оставив только левый член, содержащий выходную переменную и ее производную. «OY + a Y + ayU = b0 и 4-bx4-c0f. (2.6) Вводит обозначение p для дифференциальных операций. didt = pt df / dtl = pl Используя это, уравнение (2.6) можно записать в виде: a Q (p) (* oP2 4-flip + Людмила Фирмаль
Если ссылка (система) имеет несколько входов, оставшаяся входная величина принимается равной нулю при определении передаточной функции для одной входной величины. Найти передаточную функцию в виде изображения Лапласа ссылки, описанной в примере 2.3 (2.6). Преобразуйте обе части этого уравнения в изображение Лапласа. L (a0 V + окси-b ° * /) = L (b0 и -f-bxu -f cj I. Используя исходную линейность и производные характеристики (характеристики 1 и 2 преобразования Лапласа), при начальном условии нуля получаем: (A0s * + a, s + a2) Y (s) = (b, s + b>) U (s) + cnF ($), (2.13) Где K (s) = M Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Сходство между формой изображения Лапласа и передаточной функцией операторной формы чисто внешнее и имеет место только с фиксированными связями (системами). Уравнение (2.14) ложно, если связь нестационарная, т.е. множитель (2.6) зависит от времени. Передаточная функция (2.14) может быть использована для описания уравнения изображения Лапласа (2.13). Y (s) = Wt (s) U (s) + Wt (s) F (s). (2.15) Это уравнение, как и уравнение (2.13), подходит для исходного дифференциального уравнения (2.6) только тогда, когда начальное состояние равно нулю. Если начальное условие не равно нулю, уравнения (2.13) и (2.15) не могут использоваться в качестве математического описания начальной ссылки.
Как правило, линейные дифференциальные уравнения с постоянными коэффициентами, меньшими или равными второму порядку, записываются в стандартном виде. Кроме того, термины, которые включают в себя вывод и е Напишите производную в левой части уравнения и все остальные члены в правой части. Коэффициент выходного значения равен 1. Если справа есть производная, любая отдельная входная величина и термин, содержащий производную, объединяются в группу, а соответствующие входные количественные коэффициенты берутся из скобок.
Стандартный формат для описания линейных дифференциальных уравнений. Людмила Фирмаль
Стандартная формула формулы (2.6) принимает следующую форму: + Tree + y = kx (7> + u) + kj, (2.16) Здесь k = c0 / a. В уравнении (2.16) постоянные T0, G и T2 имеют временную размерность, они называются постоянными времени, а коэффициент и кг — коэффициенты передачи. Если исходное уравнение (2.6) не содержит y (a.g = 0), в стандартной форме производная y должна иметь коэффициент, равный 1. Обе части уравнения делятся на коэффициент а. В символической форме уравнение (2.16) принимает вид: (Подсказка * + 7> = + + kj.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Формы записи линеаризованных уравнений
В теории управления принято записывать дифференциальные уравнения в двух стандартных формах.
В общем виде линеаризованное дифференциальное уравнение, описывающее элемент, можно записать следующим образом

где y(t), x(t), f(t) — выходная и входная величины элемента и внешнее воздействие;
n — порядок уравнения, причем ( n³m,k ); это условие физической реализуемости элемента, показывающее, что сигнал на выходе реального элемента не может возникнуть раньше подачи воздействия на его вход, т.е.
Коэффициенты уравнения имеют размерности:
ai [c n — i ]; bi 

В общем случае в соответствии с (2.8) уравнение элемента можно представить в форме
D(p) y(t) = N(p) x(t) + M(p) f(t) . (2.9)



полиномы степени n, m, k от символа дифференцирования p.
Первая стандартная форма записи. Дифференциальное уравнение записывают так, чтобы выходная величина и ее производные находились в левой части уравнения, а входные величины и все остальные члены — в правой. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести уравнение (2.8) к такому виду, разделим левую и правую его части на an и получим
При записи уравнения в первой стандартной форме (2.10) получившиеся коэффициенты:
Тn , Тn-1 ,…, Т1 называются постоянными времени, они имеют размерность времени [с] и характеризуют инерционные свойства элемента; а
k1 


называются коэффициентами передачи. Они представляют собой весовые коэффициенты, показывающие какой вклад в формирование выходной величины элемента вносит каждое слагаемое правой части уравнения.
Вторая стандартная форма записи.Для решения дифференциальных уравнений широкое распространение получил операторный метод, при использовании которого задача нахождения решения дифференциального уравнения сводится к алгебраическим действиям. Чтобы перейти от исходного дифференциального уравнения элемента при нулевых начальных условиях к операторному, необходимо в дифференциальном уравнении вместо реальных функций времени записать их изображения по Лапласу, а в полиномах символ дифференцирования p заменить на оператор Лапласа s.
Применив к дифференциальному уравнению (2.9) преобразование Лапласа, получим
D(s)Y(s) = N(s) X(s) + M(s) F(s) , (2.11)
где s – оператор Лапласа;
Y(s), X(s), F(s) — изображения по Лапласу выходной и входной величин элемента и внешнего воздействия;
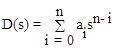

полиномы степени n, m, k от оператора Лапласа s.
Оператор Лапласа s представляет собой комплексную величину, причем s=c+jw, где:
c=Re s — абсцисса абсолютной сходимости;
w=Im s –угловая частота, имеющая размерность [рад/с];
Для перехода от реальных функций времени — оригиналов к их изображениям по Лапласу и наоборот введены прямое и обратное интегральные преобразования вида:


На практике для этих целей используют специальные таблицы [1,7].
Уравнения (2.9) и (2.11) формально совпадают между собой. Однако уравнение (2.9) является дифференциальным, куда входят реальные функции времени, а уравнение (2.11) — алгебраическим относительно изображений функций времени по Лапласу.
После ввода следующих обозначений:

уравнение (2.11) примет вид, являющийся второй стандартной формой записи
Выражения Wx(s) и Wf(s) в теории управления называются передаточными функциями.
Если f(t) = 0, то F(s) = 0 и тогда 
Eсли x(t)=0, то X(s)=0 и тогда 
Передаточная функцияэлемента по заданному входу есть отношение изображений по Лапласу его выходной и входной величин при нулевых начальных условиях и равных нулю воздействиях на остальных входах элемента.
Передаточная функция имеет важное основополагающее значение в классической теории управления. Она устанавливает связь в динамическом режиме между выходной и входной величинами элемента и полностью характеризует его динамические свойства.
Понятие передаточной функции весьма удобно при анализе так называемых структурных схем. Так, например, элемент, изображенный на рис. 2.2, после линеаризации можно представить в виде структурной схемы, показанной на рис. 2.3.
Рис. 2.3. Структурная схема элемента
Передаточные функции элементов или отдельных участков схемы позволяют легко получить общее уравнение всей системы, а в случае необходимости перейти к дифференциальному уравнению.
Замечание: в литературе часто оператор Лапласа обозначается буквой p.
Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия, которые наиболее полно отражают особенности реальных возмущений. Во — первых, это позволяет сравнивать отдельные элементы между собой с точки зрения их динамических свойств. Во — вторых, зная реакцию системы на типовые воздействия, можно судить о том, как она будет вести себя при сложных изменениях входной величины.
Наиболее распространенными типовыми воздействиями являются: ступенчатое, импульсное и гармоническое воздействия. Любой сигнал u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий ui(t) и исследовать реакцию системы на каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить результирующее изменение выходной величины y(t) суммируя полученные таким образом составляющие выходного сигнала yi(t).
Особенно важное значение в ТАУ придают ступенчатому воздействию 1(t) = 

Зависимость изменения выходной величины системы от времени при подаче на ее вход единичного ступенчатого воздействия при нулевых начальных условиях называется переходной характеристикой и обозначается h(t).
Не менее важное значение в ТАУ уделяется импульсной переходной характеристике, которая описывает реакцию системы на единичное импульсное воздействие при нулевых начальных условиях, обозначают 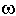
Переходная и импульсная переходная характеристики называются временными характеристиками. Каждая из них является исчерпывающей характеристиками системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно определить выходную величину при произвольном входном воздействии.
Зная передаточную функцию W(p) = K(p)/D(p), выражение для переходной функции можно найти из формулы Хевисайда: 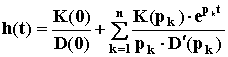
Видео:Дифференциальные уравнения. 11 класс.Скачать

Формы записи дифференциальных уравнений
Стационарные линейные непрерывные САУ наиболее часто описываются линейными дифференциальными уравнениями с постоянными коэффициентами:

В этом уравнении 




Применяется также операторная форма записи уравнения (2.9):

В этом уравнении через « 

Заметим, что по сложившейся традиции символ « 

За многолетнюю историю развития ТАУ сложились традиции формальной записи линейных дифференциальных уравнений, описывающих стационарные САУ. В учебной литературе по ТАУ они рассматриваются как стандартные формы записи дифференциальных уравнений. Рассмотрим эти формы записи на примере линейной системы второго порядка:


или в операторной форме

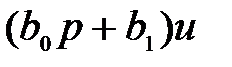
Первая стандартная символическая форма записи уравнения (2.11) имеет следующий вид:

где 



Форма (2.13) представляет собой операторно-структурное описание системы, т.е. в виде операторов звеньев, составляющих структурную схему системы (далее эти понятия разъясняются), и связей между ними. В этой форме 

Из изложенного выше следует, что уравнение (2.9) в этой форме перепишется в следующем виде:

где 


Во второй стандартной форме записи дифференциального уравнения используется передаточная функция системы, которая для рассматриваемого примера (2.11) имеет вид
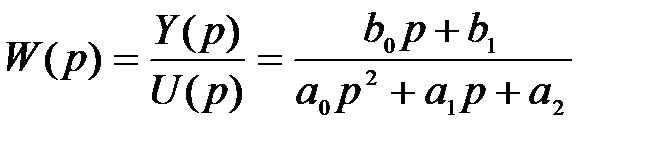
Передаточная функция САУ, поведение которой во времени описывается уравнением (2.9), имеет следующий вид :
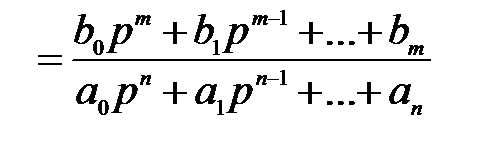
В формуле (2.15) через 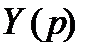




Вторая стандартная форма записи дифференциального уравнения имеет следующий вид:

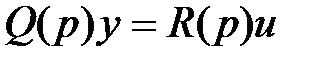
В (2.16) 


Из сравнения первой и второй стандартных форм записи дифференциальных уравнений следует, что с математической точки зрения различие между этими формами весьма несущественно и состоит лишь в различном представлении коэффициентов уравнений. В ТАУ принято называть уравнения вида (2.9) — (2.14), (2.16) уравнениями типа «вход-выход».
Третья стандартная форма записи дифференциального уравнения принципиально отличается от форм записи, описанных выше. В этой форме записи используются переменные состояния. Отметим, что понятие «состояние» является базовым в современной ТАУ (СТАУ). Переменные состояния — это промежуточные переменные системы (рис.2.2), число которых равно ее порядку 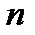
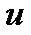



Рис.2.2 — Состояние системы | Переменные состояния называют также координатами состояния, так как их совокупность задает вектор состояния  . . |
Множество возможных положений этого вектора образует векторное пространство 
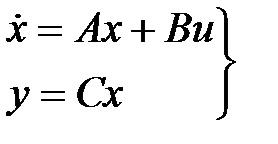
где 





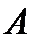
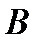

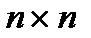


Процессы в САУ в свободном движении (без внешних воздействий) согласно уравнению (2.17) описываются векторно-матричным уравнением 


с характеристическим уравнением

Эти уравнения при определенных начальных условиях дают возможность изучить процессы в системе путем их решения численными методами с использованием ЭВМ.
Разработаны различные способы перехода от уравнений типа «вход-выход» к уравнениям состояния вида (2.17) и наоборот. Один из наиболее распространенных способов состоит в следующем. Пусть САУ описывается уравнением (2.9). Введем обозначения




С помощью этих обозначений преобразуем уравнение (3.1) к следующему виду:
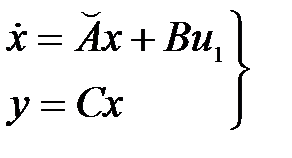
где 



В нашем примере 



Система уравнений (2.19) представляет собой описание линейной непрерывной системы в пространстве состояний 

Если 


Форма уравнений (2.19) с подобными матрицами 

Задание 1
1.1. По дифференциальному уравнению системы:
Для каждого типового звена 1 – 12 (таблицы 2.1) в соответствии с его параметрами вывести дифференциальное уравнение, операторное уравнение, и выражение передаточной функции.
1.2Математическое описание типового звена системы автоматического регулирования записать в трех формах записи дифференциальных уравнений.
Первая стандартная символическая форма операторно-структурное описание системы, т.е. в виде операторов звеньев.
Во второй стандартной форме записи дифференциального уравнения используется передаточная функция системы.
Третья стандартная форма записи дифференциального уравнения — переменные состояния.
Таблица 2.1 – Исходные коэффициенты
| № п.п. | Наименование звена | а 0 | а 1 | а 2 | b0 | b1 | Примечания |
| Безынерционное (пропорциональное) | к | ||||||
| Инерционное 1-го порядка (апериодическое) | Т | k | |||||
| Инерционное 2-го по- рядка (апериодическое) | Т2 2 | Т1 | k | Т1³2Т2 | |||
| Инерционное 2-го по- рядка (колебательное) | Т2 2 | Т1 | k | Т1 T |
Задание 2
2.1Для каждого звена (таблицы 2.2) по его передаточной функции записать дифференциальное уравнение.
2.2 Математическое описание типового звена системы автоматического регулирования записать в трех формах записи дифференциальных уравнений.
| Вар | Передаточная функция | Значения параметров передаточной функции |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; а4=0,5;в0=1;в1=3; в2=0,8;в3=0,3 | |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; в0=1;в1=3; в2=0,8 | |
 | а0=1; а1=5; а2 =1,2; в0=1; в1=3; | |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; а4=0,5; в0=10 | |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; в0=10 | |
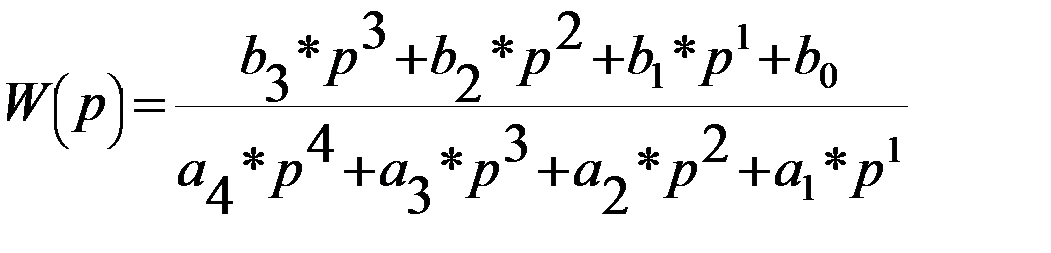 | а0=1; а1=5; а2 =1,2; а3=0,9;а4=0,5;в0=1;в1=3; в2=0,8;в3=0,3 | |
 | Т0=2; Т1=4; Т2=1,1;Т3=0,9 | |
 | Т0=2; Т1=4; Т2=1,1;Т3=1,1;Т4=,9 | |
 | К= 10;Т1=4; Т2=1,1;Т3=0,9 | |
 | К= 10; Т2=1,1;Т3=0,9 Т4=0,9 | |
 | Т0=0,7; Т1=3;Т2=1,2;Т3=0,9;Т4=0,8;Т5=0,5 | |
 | К=10 Т0=0,7; Т1=3;Т2=1,2;Т3=0,9;Т4=0,8;Т5=0,5; |
Задание №3
3.1 Для заданной схемы необходимо составить операторное уравнение для каждого элемента схемы САУ.
3.2. Определить входные и выходные величины каждого элемента, и определить передаточные функции отдельных элементов функциональной схемы.
Формы записи дифференциальных уравнений.
3.3Сформировать математическое описание систем автоматического регулирования в виде структурной схемы в буквенном и числовом обозначениях.
3.4 Сформировать математическое описание систем автоматического регулирования в виде третьей стандартной формы записи дифференциального уравнения — В переменных состояния САУ описываемых векторно-матричным уравнением.
Схема, показанная на рисунке 2.2, представляет собой САР температуры в помещении. Объектом регулирования (ОР) в данной системе является помещение, для которого регулируемая величина — температура внутри помещения Ө, регулирующее (управляющее) воздействие — температура воздуха ӨК, поступающего из калорифера, возмущающее воздействие — изменения внешних факторов f(в общем случае изменение температуры атмосферного воздуха, его влажности, скорости ветра). При исследовании системы в качестве основного возмущения следует рассматривать изменение температуры окружающего воздуха.
Воспринимающим органом — ВО (датчиком, чувствительным элементом) в данной САР является терморезистор RД, включенный в мостовую схему, обеспечивающую с помощью резистора RОзадание необходимого значения температуры в помещении и выполняющую также функции сравнивающего органа — СО (элемента сравнения). Усиление сигнала разбалансаΔU(сигнала рассогласования) измерительной мостовой схемы обеспечивается посредством усилителя. Усиленный сигнал Uобеспечивает вращение двухфазного исполнительного двигателя, который изменяет перемещение клапана (заслонки) на трубопроводе подачи парав калорифер, чем достигается изменение температуры воздуха на входе калорифера — регулирующего воздействия на объектерегулирования.
 |
1 — помещение; 2 — теплообменник (калорифер), 3 — измерительная мостовая схема; 4 — двухфазный исполнительный двигатель, 5 — дифференциальный магнитный усилитель; 6 — клапан (заслонка)
Рис. 2.2. Схема САР температуры
Динамические свойства объекта регулирования и элементов системы описываются следующими уравнениями:
где То, Т2, Т3, Т4 — постоянные времени, с; Ө — значение температуры воздуха в помещении, °С, Ө к — значение температуры воздуха на выходе калорифера, °С; к, к1, к2, к3, к4— коэффициенты передачи; f— возмущающее воздействие на объекте регулирования; Uд —падение напряжения на термодатчике, В; ΔU— напряжение на выходе мостовой схемы (сигнал рассогласования), В; μ. — линейное перемещение клапана, см; U0 — задающий сигнал, В.
Значения параметров элементов САР по вариантам даны в таблице 2.3.
Заданное значение температуры в помещении Ө = 20 °С.
Значения параметров элементов САР
| Вариант | Т0, с | Т2, с | к | к1, В/ 0 С | к4 | к2, см/(В*с) | f,. 0 С | К3, °С/см |
| 0,06 | 0,2 | 0,2 | 0,002 | -11 | ||||
| 0,07 | 0,25 | 0,3 | 0,001 | |||||
| 0,08 | 0,3 | 0,25 | 0,0018 | -8 | ||||
| 0,09 | 0,35 | 0,2 | 0,002 | |||||
| 0,10 | 0,4 | 0,2 | 0,002 | -5 | ||||
| 0,50 | 0,18 | 0,25 | 0,003 | |||||
| 0,055 | 0,19 | 0,4 | 0,0035 | |||||
| 0,06 | 0,17 | 0,4 | 0,0025 | -15 | ||||
| 0,06 | 0,25 | 0,2 | 0,0016 | |||||
| 0,08 | 0,4 | 0,15 | 0,0014 | -18 |
Примечание. Для всех вариантов постоянные времени Т3 = 20 с, Т4=0,5 с.
Схема САР, приведенная на рисунке 2.3, обеспечивает стабилизацию угловой скорости электродвигателя постоянного тока который совместно с рабочим механизмом является объектом регулирования. Регулируемая величина объекта — угловая скорость двигателя ω, регулирующее воздействие — напряжение Uг,подаваемое от генератора на якорь двигателя. Возмущающее воздействие на объекте регулирования — момент сопротивления Мс, создаваемый рабочим механизмом. Угловая скорость двигателя ωконтролируется тахогенератором, сигнал которого Uтг, пропорциональный скорости, сравнивается с задающим сигналом U3. Сигнал рассогласования ΔU = U3— UTг усиливается магнитным усилителем и воздействует на обмотку возбуждения генератора, выполняющего функции исполнительного органа (элемента).
Динамические свойства объекта регулирования и элементов САР описываются следующими уравнениями:
гдеТд, Ту, Tv — постоянные времени, с; Кд, Км, Ктг, Ку, Кг — коэффициенты передачи соответствующих элементов систем
1 — задающий потенциометр; 2 — магнитный усилитель; 3 — генератор; 4 — двигатель; 5 — тахогенератор; 6 — рабочий механизм
Рис. 2.3. Схема САР угловой скорости электродвигателя
Значения параметров элементов САР
| Вариант | Ту, с | Ку | Кг | Тг, с | Кд, рад/ с*В | Тд, с | Км рад/ с*Н* м | Мс, Н*м | Кгг, В*с/ рад |
| 0,020 | 4,0 | 2,0 | 0,10 | 1,0 | 0,5 | 0,02 | 1,0 | ||
| 0,015 | 5,0 | 1,8 | 0,12 | 0,95 | 0,60 | 0,03 | 0,9 | ||
| 0,018 | 4,5 | 1,7 | 0,15 | 0,85 | 0,70 | 0,04 | |||
| 0,022 | 6,0 | 1,5 | 0,20 | 0,8 | 0,80 | 0,05 | 0,7 | ||
| 0,020 | 5,8 | 1,6 | 0,16 | 1,5 | 0,65 | 0,06 | 0,6 | ||
| 0,025 | 4,2 | 2,0 | 0,25 | 1,4 | 0,75 | 0,07 | 0,5 | ||
| 0,020 | 3,5 | 2,7 | 0,22 | 1,3 | 0,80 | 0,08 | 0,4 | ||
| 0,028 | 6,2 | 2,1 | 0,30 | 1,2 | 0,75 | 0,02 | 0,5 | ||
| 0,018 | 6,5 | 2,3 | 0,16 | 1,0 | 0,50 | 0,013 | 0,6 | ||
| 0,014 | 7,0 | 2,5 | 0,20 | 1,25 | 0,80 | 0,015 | 0,7 |
Значения параметров объекта регулирования и элементов системы для различных вариантов указаны в таблице 2.4. Заданное значение угловой скорости ω = 40 рад/с.
На рисунке 2.4 изображена схема САР давления Р в ресивере (воздухосборнике) 1, который является в данной системе объектом регулирования. Давление в ресивере регулируется посредством изменения количества воздуха Q, зависящего от положения заслонки 2, т.е. от ее линейного перемещения Х3, которое можно рассматривать как регулирующее воздействие на входе объекта регулирования. Внешним возмущением, вызывающим отклонение регулируемой величины — давления Р, является изменение расхода сжатого воздуха Qc.
Рис 2.4 Схема САР давления Р в ресивере
Давление в данной системе контролируется с помощью сильфонного датчика 3, выходная величина которого — перемещение Хс сильфона 5 однозначно зависит от разности сил ΔF= F0— Fp, где Fp— сила, создаваемая давлением Р, F0— сила натяжения пружины 6, которое можно изменять винтом 7.
Перемещение сильфона Хсс помощью потенциометрического преобразователя 4 преобразуется в электрический сигнал — напряжение U, которое усиливается электронным усилителем 8. Выходной сигнал усилителя Uyуправляет электромагнитным приводом 9, связанным с заслонкой 2,
В данной САР сильфонный датчик выполняет функции воспринимающего, задающего и сравнивающего органов. Как воспринимающий орган он контролирует давление Р, преобразуя его в силу Fp. Задание требуемого давления в ресивере обеспечивается посредством силы F0. Как сравнивающий орган сильфон обеспечивает сравнение величин F0 и Fp, в результате чего, как отмечалось ранее, получается ΔF= F0 — Fp — сигнал рассогласования.
Динамические свойства объекта регулирования и элементов САР описываются следующей системой уравнений:
| заслонкой |
Физическая сущность переменных, входящих в уравнения, отражена выше в описании схемы САР. Параметры T0, T1, T2, T3 и К0, Кq, Кв, Кc, Кп, Ку, К3 — соответственно постоянные времени и коэффициенты передачи. Их размерности и значения по вариантам даны в таблице 2.5. Требуемое значение давления Р = 500 кПа.
Значения параметров элементов САР
| Вариант | Т0,с | Ко КПа/мм | Т1,с | Т2,с | Кс мм/Н | Кв Н/кПа | КQ, Кпа*с/м 3 | ΔQC, м3/с | Кп В/мм | Ку | Т3 | К3 Мм/В |
| 1,3 | 0,2 | 0,045 | 2,5 | 0,5 | 0,1 | 0,2 | 0,01 | |||||
| 0, 25 | 0 ,04 | 2,5 | 0,5 | -0, 2 | 0,2 | 0,01 | ||||||
| 0,6 | 3,5 | 0,34 | 0,022 | 2,5 | 0,5 | 0,3 | 0,2 | 0,01 | ||||
| 4,8 | 0,25 | 0,035 | 2,5 | 0,5 | -0,15 | 0,2 | 0,01 | |||||
| 0,7 | 4,5 | 0,3 | 0,04 | 2,5 | 0,5 | 0,12 | 0, 9 | 0,01 | ||||
| 0,8 | 3,5 | 0,18 | 0, 025 | 2 ,5 | 0,5 | -0,2 | 0 ,2 | 0,01 | ||||
| 0,4 | 4,4 | 0,25 | 0,03 | 2,5 | 0,5 | 0,11 | 0,2 | 0,01 | ||||
| 0,65 | 5,5 | 0,2 | 0,02 | 2,5 | 0,5 | -0,12 | 0,2 | 0,01 | ||||
| 0, 7 | 0, 4 | 0 ,025 | 2,5 | 0,5 | 0,14 | 0,2 | 0,01 | |||||
| 0,55 | 0,25 | 0,035 | 2,5 | 0,5 | -0,14 | 0,2 | 0,01 |
На электрических станциях при производстве электроэнергии предъявляют определенные требования к стабильности частоты f генерируемой ЭДС. Частота f однозначно определяется угловой скоростью ω рабочего колеса гидротурбины. В связи с этим гидротурбины на электростанциях оснащают САР угловой скорости. На рисунке 2.5 показана схема одного из вариантов такой САР.
В данной системе объектом регулирования является гидротурбина 1, регулируемой величиной — угловая скорость ω .Она при постоянном расходе воды изменяется в зависимости от нагрузки на валу турбины, т. е. от мощности Р, которая потребляется от генератора 2 (с увеличением мощности угловая скорость снижается, с уменьшением — возрастает). Таким образом, мощность Р является внешним возмущающим воздействием на объекте регулирования. Для регулирования угловой скорости предусмотрена заслонка 3, с помощью которой изменяется расход воды через турбину. Он однозначно зависит от вертикального перемещения X заслонки. Следовательно, перемещение заслонки X можно рассматривать как регулирующее воздействие объекта регулирования. Угловая скорость ω контролируется посредством тахогенератора 4, ЭДС Е которого сравнивается с задающим напряжением U0. Сигнал рассогласования Δ U через усилитель 5 управляет посредством электродвигателя 6 и редуктора 7 заслонкой 3.
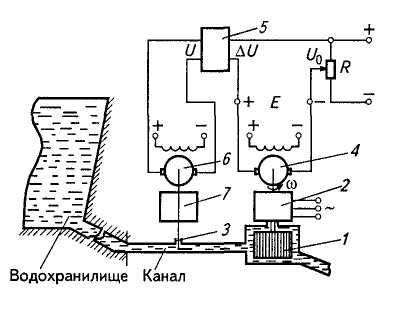 |
Рис. 2.5 Схема САР угловой скорости рабочего колеса гидротурбины
Динамические свойства элементов САР описываются следующей системой уравнений:
💥 Видео
Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

1. Что такое дифференциальное уравнение?Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Шапошников С. В. - Математический анализ. Часть 4 - Дифференциальные 1 и 2-формыСкачать

Матричная форма записи системы линейных уравненийСкачать

Лекция. Передаточная функция, стандартная форма записиСкачать

Задача Коши для дифференциальных уравненийСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

ДОЭФ 2015. Лекция 0 (Дифференциальные уравнения)Скачать