Помимо классического метода наименьших квадратов для определения неизвестных параметров линейной модели множественной регрессии β0…βm используется метод оценки данных параметров через β-коэффициенты (коэффициенты модели регрессии в стандартных масштабах).
Построение модели множественной регрессии в стандартизированном или нормированном масштабе означает, что все переменные, включенные в модель регрессии, стандартизируются с помощью специальных формул.
Посредством процесса стандартизации точкой отсчёта для каждой нормированной переменной устанавливается её среднее значение по выборочной совокупности. При этом в качестве единицы измерения стандартизированной переменной принимается её среднеквадратическое отклонение σ.
Факторная переменная х переводится в стандартизированный масштаб по формуле:
где xij – значение переменной xjв i-том наблюдении;
G(xj) – среднеквадратическое отклонение факторной переменной xi;
Результативная переменная у переводится в стандартизированный масштаб по формуле:
где G(y) – среднеквадратическое отклонение результативной переменной у.
Если между исследуемыми переменными в исходном масштабе является линейной, то процесс стандартизации не нарушает этой связи, поэтому стандартизированные переменные будут связаны между собой линейно:
Неизвестные коэффициенты данной функции можно определить с помощью классического метода наименьших квадратов для линейной модели множественной регрессии. В этом случае минимизируется функционал F вида:
В результате минимизации данного функционала получим систему нормальных уравнений, переменными в которой будут являться парные коэффициенты корреляции между факторными и результативной переменной. Такой подход основывается на следующем равенстве:
Система нормальных уравнений для стандартизированной модели множественной регрессии имеет вид:
В связи с тем, что полученная система нормальных уравнений является квадратной (количество уравнений равняется количеству неизвестных переменных), то оценки коэффициентов
можно рассчитать с помощью метода Крамера, метода Гаусса или метода обратных матриц.
Рассчитанные из системы нормальных уравнений β-коэффициенты в стандартизированном масштабе необходимо перевести в масштаб исходных данных по формулам:
Рассмотрим метод Гаусса решения квадратных систем линейных уравнений. Суть данного метода заключается в том, что исходная квадратная система из n линейных уравнений с n неизвестными переменными преобразовывают к треугольному виду. Для этого в одном и уавнений системы оставляют все неизвестные переменные. В другом уравнении сокращают одну из неизвестных переменных для того, чтобы число неизвестных стало (n-1). В следующем уравнении сокращают две неизвестных переменных, чтобы число переменных стало (n-2). В результате данных преобразований исходная система уравнений примет треугольный вид, первое уравнение которой содержит все неизвестные, а последнее – только одну. В последнем уравнении системы остаётся (n-(n-1)) неизвестных переменных, т. е. одна неизвестная переменная, которая называется базисной. Дальнейшее решение сводится к выражению свободных (n-1) неизвестных переменных через базисную переменную и получению общего решения квадратной системы линейных уравнений.
Видео:Множественная регрессияСкачать

Построение уравнения регрессии в стандартизованном масштабе
4.2 Построение уравнения регрессии в стандартизованном масштабе
Параметры множественной регрессии можно определить другим способом, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:
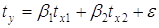
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида:
где rух1, rух2 – парные коэффициенты корреляции.
Парные коэффициенты корреляции найдем по формулам:
Система уравнений имеет вид:
Решив систему методом определителей, получили формулы:
Уравнение в стандартизированном масштабе имеет вид:
Таким образом, с ростом уровня бедности на 1 сигму при неизменном среднедушевом доходе населения, общий коэффициент рождаемости уменьшится на 0,075 сигмы; а с увеличением среднедушевого дохода населения на 1 сигму при неизменном уровне бедности, общий коэффициент рождаемости возрастет на 0,465 сигмы.
Во множественной регрессии коэффициенты «чистой» регрессии bi связаны со стандартизованными коэффициентами регрессии βi следующим образом:
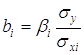
5. Частные уравнения регрессии
5.1 Построение частных уравнений регрессии
Частные уравнения регрессии связывают результативный признак с соответствующими факторами х при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения имеют вид:
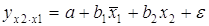
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, т.к. другие факторы закреплены на неизменном уровне.
В данной задаче частные уравнения имеют вид:
5.2 Определение частных коэффициентов эластичности
На основе частных уравнений регрессии можно определить частные коэффициенты эластичности для каждого региона по формуле:
Рассчитаем частные коэффициенты эластичности для Калининградской и Ленинградской областей.
Для Калининградской области х1=11,4, х2=12,4, тогда:
Для Ленинградской области х1 =10,6, х2=12,6:
Таким образом, в Калининградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,07%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,148%. В Ленинградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,065%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,15%.
5.3 Определение средних коэффициентов эластичности
Средние по совокупности показатели эластичности находим по формуле:
Для данной задачи они окажутся равными:
Таким образом, с ростом уровня бедности на 1%, общий коэффициент рождаемости в среднем по совокупности сократится на 0,054% при неизменном среднедушевом доходе. При увеличении среднедушевого дохода на 1%, общий коэффициент рождаемости в среднем по изучаемой совокупности возрастет на 0,209% при неизменном уровне бедности.
6. Множественная корреляция
6.1 Коэффициент множественной корреляции
Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, т.е. оценивает тесноту связи совместного влияния факторов на результат.
Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции. При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:
Ryx1x2 =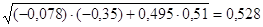
Таким образом, связь общего коэффициента рождаемости с уровнем бедности и среднедушевым доходом слабая.
Видео:Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

уравнение множественной регрессии в натуральном и стандартизированном виде
Оценка параметров уравнения регресии в стандартизованном масштабе
Параметры уравнения множественной регрессии в задачах по эконометрике оценивают аналогично парной регрессии, методом наименьших квадратов (МНК). При применении этого метода строится система нормальных уравнений, решение которой и позволяет получать оценки параметров регрессии.
При определении параметров уравнения множественной регрессии на основе матрицы парных коэффициентов корреляции строим уравнение регрессии в стандартизованном масштабе:
в уравнении стандартизированные переменные
Применяя метод МНК к моделям множественной регрессии в стандартизованном масштабе, после опрделенных преобразований получим систему нормальных уравнений вида
Решая системы методом определителей, находим параметры — стандартизованные коэффициенты регрессии (бета — коэффициенты). Сравнивая коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом заключается основное достоинство стандартизованных коэффициентов в отличие от обычных коэффициентов регрессии, которые несравнимы между собой.
В парной зависимости стандартизованный коэффициент регрессии связан с соответствующим коэфициентом уравнения зависимостью
Это позволяет от уравнения в стандартизованном масштабе переходить к регрессионному уравнению в натуральном масштабе переменных:
Параметр а определяется из следующего уравнения
Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор xj изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все перемеyные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии сравнимы между собой.
Рассмотренный смысл стандартизованных коэффициентов позволяет использовать их при отсеве факторов, исключая из модели факторы с наименьшим значением.
Компьютерные программы построения уравнения множественной регрессии позволяют получать либо только уравнение регрессии для исходных данных и уравнение регрессии в стандартизованном масштабе.
19. Характеристика эластичности по модели множественной регрессии. СТР 132-136
20. Взаимосвязь стандартизированных коэффициентов регрессии и коэффициентов эластичности. СТР 120-124
21. Показатели множественной и частной корреляции. Их роль при построении эконометрических моделей
Корреляция—это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой Корреляции двух случайных величин служит коэффициент Корреляции. Понятие корреляции появилось в середине XIX века в работах английских статистиков Ф. Гальтона и К. Пирсона.
Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей:
где σ 2 — общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов;
σост 2 — остаточная дисперсия в ряду у, отражающая влияния всех факторов, кроме х;
у — среднее значение результативного показателя, вычисленное по исходным наблюдениям;
s — среднее значение результативного показателя, вычисленное по уравнению регрессии.
Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем зависимость меньше. При значении R 0,6 говорят о наличии существенной связи.
Квадрат коэффициента множественной корреляции называется коэффициентом детерминации (D): D = R 2 . Коэффициент детерминации показывает, какая доля вариации результативного показателя связана с вариацией факторных показателей. В основе расчета коэффициента детерминации и коэффициента множественной корреляции лежит правило сложения дисперсий, согласно которому общая дисперсия (σ 2 ) равна сумме межгрупповой дисперсии (δ 2 ) и средней из групповых дисперсий σi 2 ):
Межгрупповая дисперсия характеризует колеблемость результативного показателя за счет изучаемого фактора, а средняя из групповых дисперсий отражает колеблемость результативного показателя за счет всех прочих факторов, кроме изучаемого.
Показатели частной корреляции. Основаны на соотношении сокращения остаточной вариации за счет дополнительно включенного в модель фактора к остаточной вариации до включения в модель соответствующего фактора
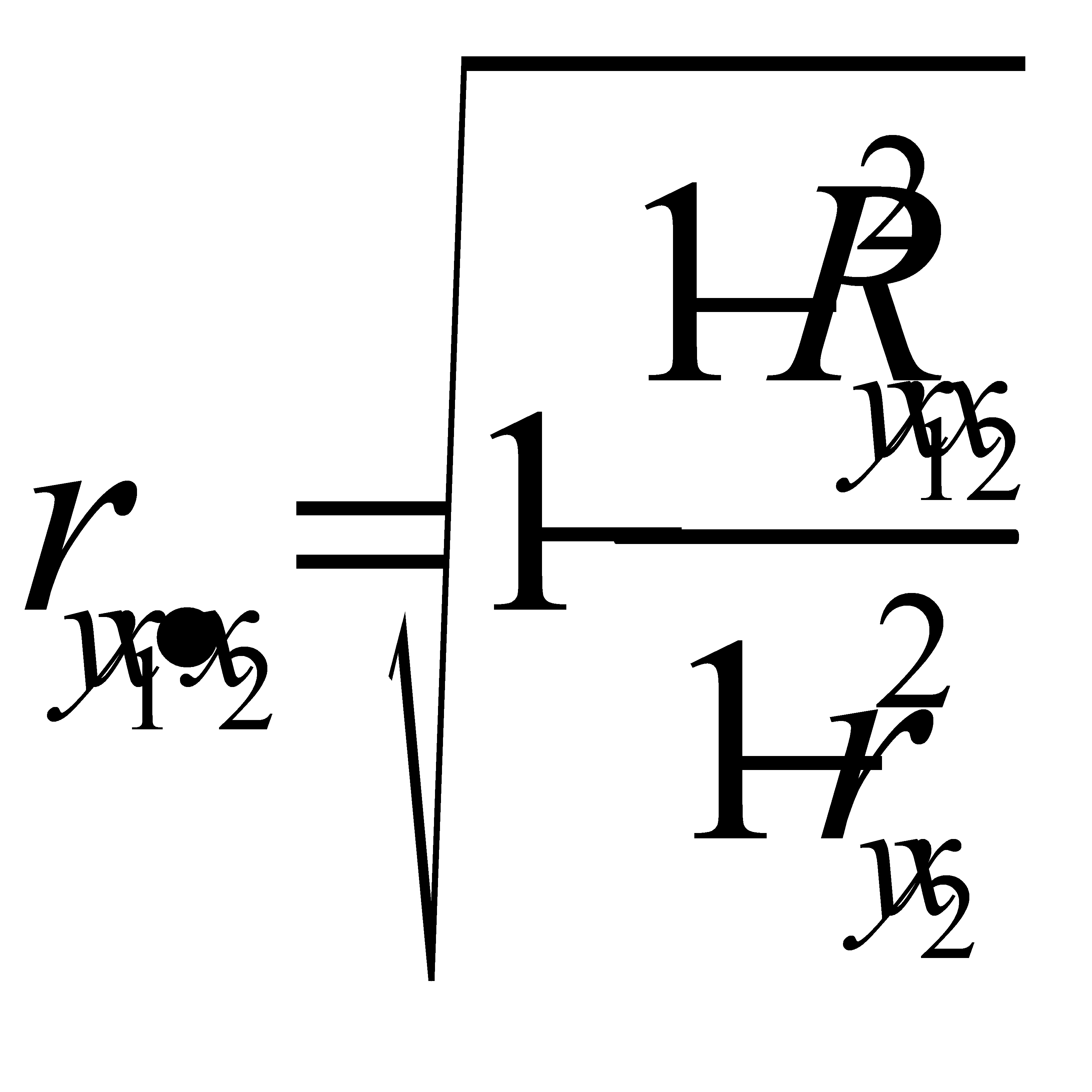
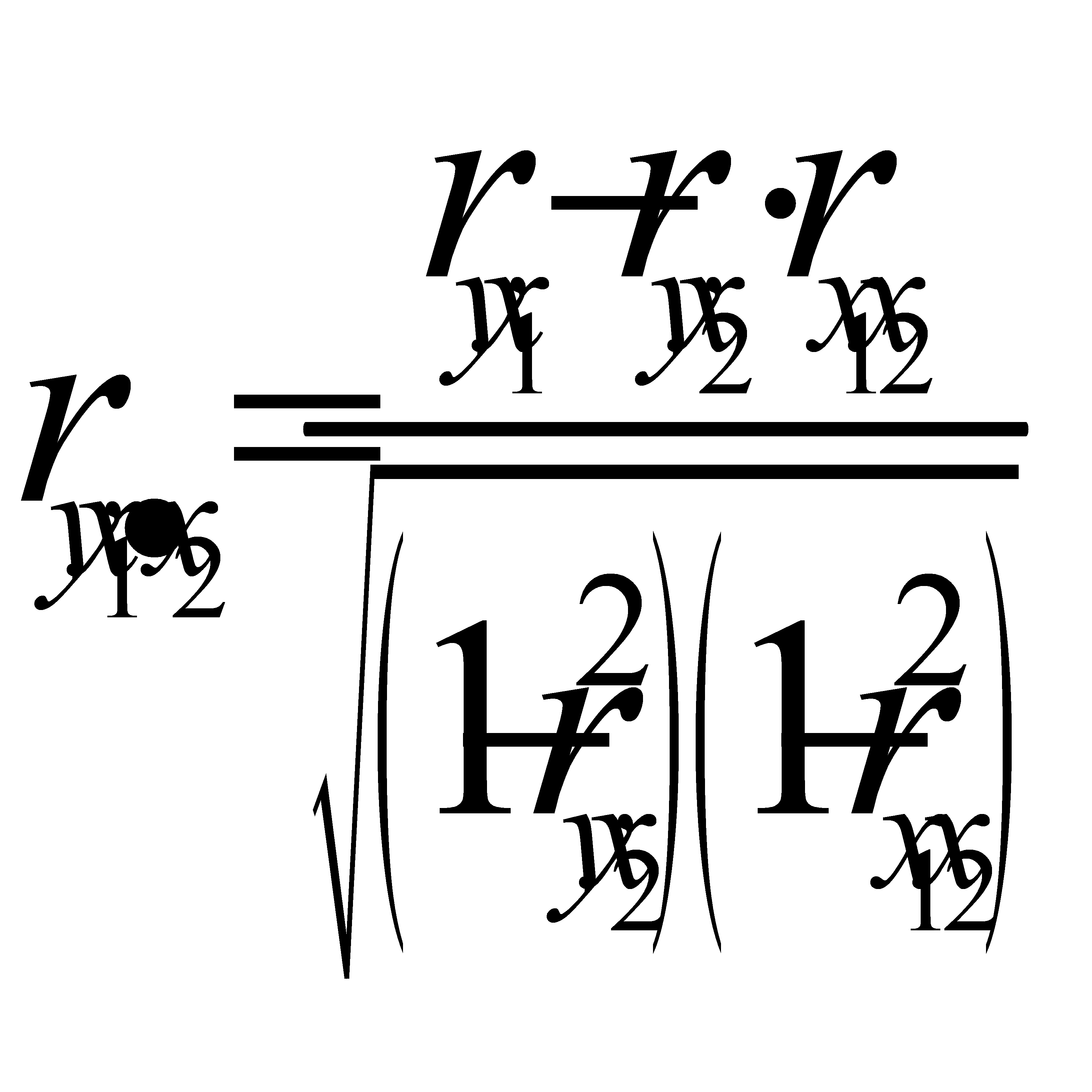

Рассмотренные показатели можно также использовать для сравнения факторов, т.е. Можно ранжировать факторы(т.е.2ой фактор более тесно связан).
Частные коэффициенты могут быть использованы в процедуре отсева факторов при построении модели.
Рассмотренные выше показатели являются коэф-ми корреляции первого порядка,т.е.они характризуют связь между двумя факторами при закреплении одного фактора (yx1.x2). Однако можно построить коэф-ты 2го и более порядка (yx1.x2x3, yx1.x2x3x4).
22. Оценка надежности результатов множественной регрессии.
Коэфициенты структурной модели могут быть оценены разными способами в зависимости от вида одновренных уравнений.
Методы оценивания коэф-тов структурной модели:
1) Косвенный МНК(КМНК)
4)МНП с полной информацией
5)МНП при огранич. информации
КМНК применяется в случаеточнойидентификацииструктурноймодели.
Процедуры примения КМНК:
1. Структурн. модель преобраз. в привед. форму модели.
2. Для каждого уравнения привед.форма модели обычным МНК оцениваются привед. коэф
3. Коэфициенты приведенной формы модели трансформируются в параметры структурной модели.
Еслиси стема сверхидентифицируема, то КМНК не исп, так как не дает однозначных оценок для параметров структурной модели. В этом случае могут исп. разные методы оценивания, среди которых наиболее распространен ДМНК.
Основная идея ДМНК на основе приведенной модели получить для сверхидентиф. уравнения теор. значения эндогенных переменных, содерж. в правой части ур-ния. Далее подставив в найденные значения вместо факт.значений применяется обычный МНК и структурн. форма сверхидент. ур-ния.
1 шаг: при опред.привед. формы модели и нахождении на ее основе оценок теор. значений эндогенной переменой
2 шаг: Применительно к структурному сверхидентифицируемому уравнению при определении структурных коэфициентов модели по данным теоритических значений эндогенных переменных.
23. Дисперсионный анализ результатов множественной регрессии.

| таблица дисперсионного анализа | ||||
| Вару | df | СКО,S | Дисп на одну df,S 2 | Fфакт |
 общ общ | n-1 | dy 2 * n | — | — |
| факт | m | dy 2 * n*R 2 yx1x2 | 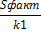 |  |
| Ост | n-m-1 | dy 2 * n*(1-R 2 yx1x2) =Sобщ-Sфакт | 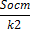 | — |
Также можно построить таблицу частного дисперсионного анализа, и найти частный F крит который оценивает целесообразность включения фактора в модель после включения др переменной
| Вариация у | df | S | S^2 |
| общая | df=n-1 | d 2 у*n | — |
| факторная | k1=m | d 2 у*n*R 2 | Sфакт/k1 |
| в том числе: | |||
| за счет x2 | d 2 у*n*r 2 yx2 | Sфактx2/1 | |
| за счет доп включ. х1 | Sфакт-Sфактх2 | Sфактx1/1 | |
| Остаточная | k2=n-m | Sобщ-Sфакт |
24. Частный F-критерий Фишера, t- критерий Стьюдента. Их роль в построении регрессионных моделей.
Для оценки статистич целесообразности добавления нов факторов в регрессион модель исп-ся частн критерий Фишера, т.к на рез-ты регрессион анализа влияет не только состав факторов, но и последовательность включения фактора в модель. Это обьясняется наличием связи между факторами.
Fxj =( (R 2 по yx1x2. xm – R 2 по yx1x2…xj-1,хj+1…xm)/(1- R 2 по yx1x2. xm) )*( (n-m-1)/1)
Fтабл (альфа,1, n-m-1) Fxj больше Fтабл – фактор xj целесообразно лючать в модель после др.факторов.
Если рассматривается уравнение y=a+b1x1+b2+b3x3+e, то определяются последовательно F-критерий для уравнения с одним фактором х1, далее F- критерий для дополнительного включения в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3, т.е. дается оценка значимости фактора х3 после включения в модель факторов x1 их2. В этом случае F-критерий для дополнительного включения фактора х2 после х1 является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х3, который является частным F- критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. С t-критерием Стьюдента связан именно частный F- критерий. Последовательный F-критерий может интересовать исследователя настадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценка значимости коэффициентов регрессии Ь1,Ь2,,b3 предполагает расчет трех межфакторных коэффициентов детерминации.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдентаи доверительные интервалыкаждого из показателей.




Если t табл. tфакт. то гипотеза H0 не отклоняется и признается случайная природа формирования a, b или rху.
25. Оценка качества регрессионных моделей. Стандартная ошибка линии регрессии.
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения 



Если это так, то большая часть вариации 
Долю общей дисперсии 
Разность 
Нет формального теста для оценки 
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования 

Мы предсказываем среднюю величину 
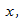

Итак, если 



Повторение этой процедуры для различных величин 
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования 

Мы предсказываем среднюю величину 
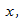

Итак, если 



Повторение этой процедуры для различных величин 
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
26. Взаимосвязь частного F-критерия, t- критерия Стьюдента и частного коэффициента корреляции.
Ввиду корреляции м/у факторами значимость одного и того же фактора м/б различной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частый F-критерий, т.е. Fxi. В общем виде для фактора xi частый F-критерий определяется как :
Если рассматривается уравнение y=a+b1x1+b2+b3x3+e, то определяются последовательно F-критерий для уравнения с одним фактором х1, далее F-критерий для дополнительного включения в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3, т. е. дается оценка значимости фактора х3 после включения в модель факторов x1 их2. В этом случае F-критерий для дополнительного включения фактора х2 после х1является последовательнымв отличие от F-критерия для дополнительного включения в модель фактора х3, который является частнымF-критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя на стадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценка значимости коэффициентов регрессии Ь1,Ь2,,b3 предполагает расчет трех межфакторных коэффициентов детерминации, а именно: 



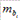
27. Варианты построения регрессионной модели. Их краткая характеристика.
28. Интерпретация параметров линейной и нелинейной регрессии.
| b | a | ||||||||||||||||||||||
| парная | линейная | Коэффициент регрессии b показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе – обратная | не интерпретируется, только знак >0 – рез-т изменяется медленнее фактора, * предполагают наличие положительной или отрицательной автокорреляции в остатках. Затем по спец. таблицам определяютсякритические значения критерия Дарбина — Уотсона dL и du для заданного числа наблюдений n, числа независимых переменных модели k при уровня значимости ɑ (обычно 0,95). По этим значениям промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1-ɑ) представлено на след: рисунке:
Если фактич. значение критерия Дарбина — Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и гипотезу Н0 отклоняют. 34. Выбор наилучшего варианта модели регрессии. 35. Нелинейные модели множественной регрессии, их общая характеристика. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы Различают два класса нелинейных регрессий: • регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; • регрессии, нелинейные по оцениваемым параметрам.
К нелинейным регрессиям по оцениваемым параметрам относятся функции: 36. Модели гиперболического типа. Кривые Энгеля, кривая Филипса, и другие примеры использования моделей данного типа. Кривые Энгеля (Engel curve) иллюстрируют зависимость между объемом потребления благ (C) и доходом потребителя (I) при неизменных ценах и предпочтениях. Названа в честь немецкого статистика Эрнста Энгеля, занимавшегося анализом влияния изменения дохода на структуру потребительских расходов.
На оси абсцисс откладывается уровень дохода потребителя, а на оси ординат — расходы на потребление данного блага. На графике показан примерный вид кривых Энгеля:
Кривая филипса отражает взаимосвязь между темпами инфляции ибезработицы. Кейнсианская модель экономики показывает, что в экономике может возникнуть либо безработица (вызванная спадом производства, следовательно уменьшением спроса на рабочую силу), либо инфляция (если экономика функционирует в состоянии полной занятости). Одновременно высокая инфляция и высокая безработица существовать не могут. Кривая Филипса была построена А.У. Филлипсом на основе данных заработной платы и безработицы в Великобритании за 1861-1957 годы. Следуя кривой Филлипса государство может выстроить свою экономическую политику. Государство с помощью стимулирования совокупного спроса может увеличить инфляцию и снизить безработицу и наоборот. Кривая Филипса была полностью верна до середины 70х годов. В этот период случилась стагнация (одновременный рост инфляции и безработицы), которую кривая филипса не смогла объяснить. 📸 ВидеоМножественная регрессия в ExcelСкачать  Статистическая функция ЛИНЕЙН. Множественная регрессия EXCEL.Скачать  Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать  Эконометрика. Множественная регрессия и корреляция.Скачать  Множественная регрессия в Excel и мультиколлинеарностьСкачать  09 02 Основы множественной регрессииСкачать  Уравнение множественной регрессии в ExcelСкачать  Множественная регрессия в программе Statistica (Multiple regression)Скачать  Построение модели множественной регрессии в программе GretlСкачать  Множественная степенная регрессияСкачать  Уравнение множественной регрессии в Excel (устар.)Скачать  Множественная Линейная Регрессия || Машинное ОбучениеСкачать  Эконометрика. Линейная парная регрессияСкачать  Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать  Множественная регрессия в программе SPSS (Multiple regression)Скачать  EViews. Урок 1. Построение модели множественной регрессии.Скачать  Эконометрика. Построение модели множественной регрессии в Excel.Скачать  Эконометрика 08 Множественная регрессияСкачать  |
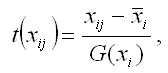
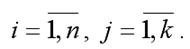
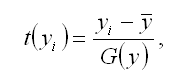
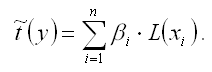
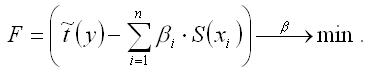
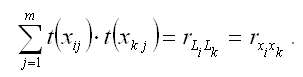
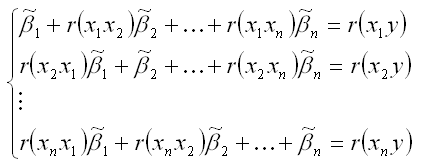
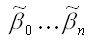
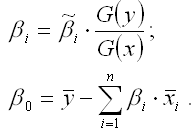

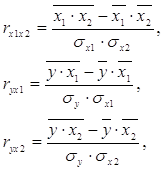


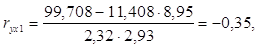
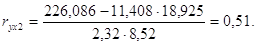
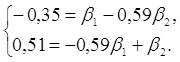
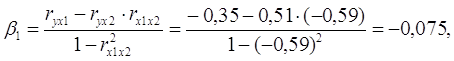
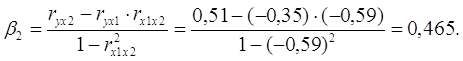
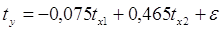
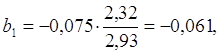
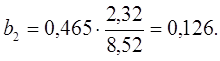
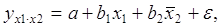
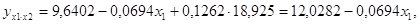
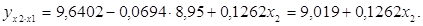
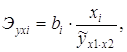
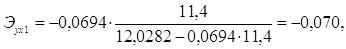
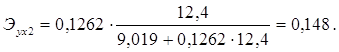
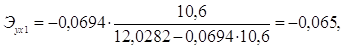
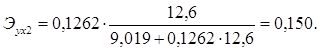
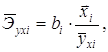
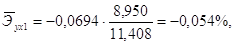
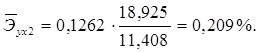
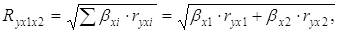










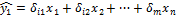









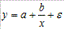 , параболы второй степени
, параболы второй степени 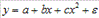 и д.р.
и д.р.
