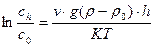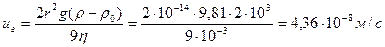Количественной характеристикой броуновского движения принято считать средний сдвиг Dх частицы за время t, т. е. наблюдаемую проекцию отрезка прямой, соединяющей начальную точку движения (при t = 0), с положением частицы в момент t, на горизонтальную плоскость (рис. 7.1).
 |
Рис. 7.1. Средний сдвиг частицы при броуновском движении
Поскольку перемещение каждой частицы случайно, среднее арифметическое смещение всех частиц при достаточно большом их числе оказывается равным нулю (в отсутствие направленного потока жидкости или градиента концентрации дисперсной фазы). Однако частицы движутся, и каждая из них уходит от исходного положения. Поэтому при изучении диффузии производится усреднение таким образом, чтобы смещения в различных направлениях не вычитались, а складывались. А именно, усредняются квадраты проекций смещения. При этом получается предложенная А. Эйнштейном величина, называемая средним квадратичным сдвигом Dх 2 . В отличие от реального пути частицы, изменяющего направление до »10 20 раз в секунду, усреднённая величина Dх 2 может быть точно вычислена на основании законов статистики. Для сферической частицы с радиусом r она прямо пропорциональна абсолютной температуре Т и времени наблюдения t и обратно пропорциональна коэффициенту Стоксагидродинамического (вязкого) сопротивления среды B = 6phr:
,
где К – коэффициент пропорциональности, в соответствии с теорией Эйнштейна равный
(k – константа Больцмана). Отсюда получаем уравнение Эйнштейна – Смолуховскогодля величины среднего квадратичного сдвига
или для среднего сдвига
.
где D — коэффициент диффузии частиц данного вещества в данной среде.
94. Осмотическое давление коллоидных растворов.Осмотический метод определения размеров коллоидных частиц.
Т. Грэму при исследовании коллоидных растворов не удалось обнаружить у них осмотического давления. Этот факт он положил в основу деления растворов на коллоидные и истинные. Однако более поздние исследования показали, что и в коллоидных системах можно наблюдать измеримое, хотя и очень малое по величине осмотическое давление.
Для истинных растворов в соответствии с законом Вант-Гоффа осмотическое давление p может быть рассчитано по уравнению
,
где C — молярная концентрация растворённого вещества.
В дисперсных системах концентрацию дисперсной фазы принято выражать числом частиц (мицелл), содержащихся в единице объёма. Эта величина называется численной или частичной концентрацией и обозначается n. Выведем соотношение между молярной концентрацией вещества в растворе и числом частиц, из которых оно состоит. Молярная концентрация представляет собой отношение количества вещества в молях к объёму раствора:
.
Выражая количество молей через число молекул, содержащихся в нём, получим
,
а так как x/V = n (n — объёмная концентрация молекул), то
.
Если же под С подразумевается молярная концентрация коллоидных частиц, тогда n — объёмная концентрация этих частиц, или, иначе, частичная концентрация золя.
Поэтому уравнение для осмотического давления коллоидных растворов будет выглядеть так:
или 
,
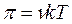
где k – константа Больцмана.
Из этого уравнения следует, что осмотическое давление увеличивается с ростом числа частиц в единице объёма даже при постоянной массе дисперсной фазы (с ростом дисперсности, например, при пептизации). Так как при одинаковой массовой концентрации n зависит от объёма частиц, то можно сказать, что осмотическое давление дисперсных (коллоидных) систем обратно пропорционально кубу радиуса их частиц.
Таким образом, закон Вант-Гоффа справедлив и для лиозолей. Однако простой расчёт показывает, что при одинаковой массовой концентрации частичные концентрации золей и тем более грубодисперсных систем обычно очень малы по сравнению с концентрацией молекул в истинных растворах. Поэтому в соответствии с выведенным уравнением и осмотическое давление в них должно быть намного меньше, а именно, во столько раз, во сколько раз частица дисперсной фазы больше, чем отдельная молекула или ион. Так, осмотическое давление коллоидных растворов в сотни и тысячи раз меньше, чем у истинных растворов. Столь малые значения очень трудно измерить с необходимой точностью, а в грубодисперсных суспензиях, пастах и эмульсиях осмотическое давление практически отсутствует.
Следует, однако, помнить, что речь идёт только об осмотическом давлении, обусловленном частицами дисперсной фазы. Надо учитывать, что в коллоидных растворах и в других дисперсных системах обычно присутствуют растворённые низкомолекулярные вещества – или в виде примесей, или в качестве стабилизаторов. Они тоже вносят свой вклад в общее осмотическое давление, поэтому его реальное значение несколько выше, чем рассчитанное исходя только из концентрации частиц дисперсной фазы.
Ещё одной особенностью осмотического давления золей является его непостоянство. Из-за идущих в той или иной степени процессов скрытой коагуляции частичная концентрация всё время уменьшается, что и вызывает снижение p во времени.
Низкое осмотическое давление является одной из причин лечебного, в частности, обеззараживающего или вяжущего действия коллоидных лекарственных средств – колларгола, протаргола и т. п. При соприкосновении их с клетками, в том числе с микробными, начинается интенсивный осмотический приток воды внутрь клеток, что приводит к гибели микробов вследствие лизиса.
Последнее изменение этой страницы: 2017-03-17; Просмотров: 2710; Нарушение авторского права страницы
Видео:10. Разложение квадратного многочлена на множителиСкачать
7 Молекулярно-кинетические свойства дисперсных систем
7 Молекулярно-кинетические свойства дисперсных систем
7.1 Примеры решения задач
Пример 1. Концентрация золя серебра равна 0,5% по массе, плотность чистого серебра 10,5г/см3, а плотность золя можно принять равной единице. Считая, что коллоидные частички золя имеют форму правильных кубиков с длиной ребра 1∙10-6 см, вычислить массу их одного моля и молярную концентрацию золя. Вычислить также осмотическое давление золя при 25°С.
Объем каждой частички серебра
Vч = l3 = (1∙10-6)3 = 1∙10-18 см3,
а ее масса mч = rчVч = 10,5∙1∙10-18 = 1,05-17г.
Масса одного моля частиц золя M = mч∙Na = 1,05∙10-17∙6,02×1023×= 6,321∙106 г/моль.
Поскольку в 1л золя массой 1000г содержится серебра 0,5∙10-2∙1000 = 5г, молярная концентрация золя CМ = 
моль/л =
Осмотическое давление золя p = СМRT = 7,91∙10-4∙8,314∙298 = 1,96Па.
Пример 2. Вычислить коэффициент диффузии сферических коллоид-ных частиц, диаметр которых равен 2∙10-6см, если температура равна 20°С, а вязкость золя не отличается от вязкости воды, равной 1∙10-3 Па∙с.
В соответствии с уравнением Эйнштейна 
коэффициент диффузии для сферических коллоидных частиц
=2,1510-4см2/с.
Пример 3. Среднеквадратичное смещение 
частицы яичного альбумина за 30 с равно 6∙10-3 см. Вычислить коэффициент диффузии при 20°С.
Из уравнения 
= 2D∙t
коэффициент диффузии D =
/2t = (6∙10-3)2/(2∙30) = 36∙10-6/600 = 6∙10-8 см2/с = 6 10-12 м2/с.
Пример 4. Вычислить скорость оседания в гравитационном поле эмульсии ртути в воде, если диаметр капель ртути равен 10-4 см, плотность ртути 13,6 г/см3, вязкость эмульсии принять равной вязкости воды 1∙10-3 Па∙с.
По уравнению uсед = 
.
см/с.
7.2 Задачи для самостоятельного решения
1. Вычислите средний квадратичный сдвиг коллоидных частиц радиусом r при броуновском движении за время τ при вязкости среды η и температуре Т. Данные для расчета приведены в таблице.
Радиус частиц, м
2. Вычислите средний квадратичный сдвиг частиц гидрозоля гидроксида железа (III) за 10с, если радиус частиц равен 50 мкм, вязкость воды 10−3 Па∙с, температура 20°С.
3. При 273К средний сдвиг частиц дыма хлорида аммония в воздухе за 5с равен 10,8∙10-4 см. Вязкость воздуха 17∙10-6 Па∙с. Определите размер частиц.
4. Средний сдвиг коллоидных частиц гидроксида железа (III) в воде при 20 С за 4с равен 13,1∙10-4 см. Вязкость воды 0,001Па∙с. Определите размер частиц.
5. При 15°С средний сдвиг частиц эмульсии соснового масла в воде за 1 с равен 0,26∙10-4 см. Вязкость воды 0,0012 Па∙с. Определите размер частиц.
6. При 25°С средний сдвиг частиц пыли в воздухе металлургического завода за 5 с равен 5,2∙10-4 см. Вязкость воздуха 17∙10-6 Па∙с. Определите размер частиц.
7. При 25°С средний сдвиг частиц слива сгустителя за 10 с равен 4,8∙10-4 см. Вязкость раствора 8,9∙10-4 Па∙с. Определите крупность слива.
8. Для частиц гуммигута радиусом 1∙10-6 см средний сдвиг в воде за 4с при температуре 25°С равен 13,1∙10-4 см. Вязкость воды 0,001 Па∙с. Вычислите число Авогадро.
9. Для частиц золя золота радиусом 2,9∙10-6 см за 3 с при температуре 20°С средний сдвиг в воде составил 6,6∙10-6 см. Вязкость воды равна 0,001 Па∙с. Вычислите число Авогадро.
10. За 16 с средний сдвиг частиц гидроксида железа (III) радиусом 1×10-6 см в воде (вязкость 0,001Па∙с) при 293 К составил 26,2∙10-4 см. Вычислите число Авогадро.
11. Средний сдвиг частиц дисперсной фазы в воздухе примерно в 8 раз больше, чем в воде. Вычислите вязкость воздуха, принимая вязкость воды равной 0,001Па∙с.
12. Во сколько раз различаются значения среднего сдвига для частиц с радиусами r1 = 2∙10-6 м и r2 =2∙10-8м?
13. Во сколько раз различаются значения коэффициента диффузии для частиц с радиусами r1 = 2∙10 -6 м и r2 =2∙10-8м?
14. При температуре 25°С за 60с средний×сдвиг частиц золя золота в воде составил 10,6∙10-4 см. Вязкость среды 0,001 Пас. Вычислите диаметр частиц.
15. Среднее смещение коллоидных частиц платины в ацетоне при температуре 17°С за 16 с составило 6,2·10−6 м. Вязкость ацетона при заданной температуре η = 3,2·10−4 Па·с. Вычислите радиус частиц золя платины и их коэффициент диффузии.
16. Рассчитайте коэффициент диффузии коллоидных частиц радиуса r при вязкости среды η и температуре Т. Данные для расчета приведены в таблице.
Мицеллы мыла в воде
Суспензия глины в воде
17. Коэффициент диффузии коллоидных частиц золота в воде при 298К равен 2,7∙10−6 м2/сут. Определите дисперсность частиц гидрозоля золота. Вязкость воды при 298К равна 0,894∙10−3 Па∙с.
18. Определите частичную концентрацию гидрозоля Al2O3, если его массовая концентрация 0,3г/л, коэффициент диффузии сферических частиц золя равен 2∙10−6м2/сут. при 293 К, плотность Al2O3 равна 4г/см3, вязкость дисперсионной среды 1∙10−3 Па∙с.
19. При 20°С и концентрации дисперсной фазы золя золота в воде 2 г/л диаметр сферических дисперсных частиц равен 60∙10-8 см, а плотность золота 19,3 г/см3. Вычислите осмотическое давление золя.
20. Вычислите осмотическое давление гидрозоля золота концентрации 2кг/м3 с диаметром частиц 6∙10−9 м и полностью 19,3∙103 кг/м3 при температуре 293К.
21. Вычислите осмотическое давление золя золота при 20°С, если массовая концентрация частиц золя равна 0,5 кг/м3, диаметр частиц равен 2·10−9 м, плотность золота равна 19,6·103 кг/м3.
22. Чему равно осмотическое давление коллоидного раствора меди при 19°С, если массовая концентрация частиц золя меди равна 0,084 кг/м3, длина ребра кубической частицы равна 1,35·10−9 м, плотность меди составляет 8,93·103 кг/м3.
23. Концентрация водного раствора миоглобина равна 10 г/л при температуре 37°С. Молекулярная масса миоглобина равна 17200 а. е.м. Вычислите осмотическое давление водного раствора миоглобина.
24. Вычислите осмотическое давление 30%-ного гидрозоля диоксида кремния при 293К, если удельная поверхность частиц золя равна 2,7∙105 м2/кг. Плотность частиц равна 2260кг/м3, плотность воды − 1000кг/м3.
25. При концентрации дисперсной фазы 5 г/л и температуре 20°С осмотическое давление золя As2S3 составляет 0,025 мм рт. ст. Плотность As2S3 равна 2,8 г/см3. Вычислите средний радиус частиц золя.
26. При 25°С и концентрации частиц золота в воде 0,5г/л осмотическое давление золя составляет 0,2 мм рт. ст. Плотность золота 19,3 г/см3. Каков средний диаметр золя частиц золота в золе?
27. Осмотическое давление золя золота в воде при среднем диаметре частиц 3∙10-7см и при 20°С равно 0,11 мм рт. ст. Плотность золота 19,3г/см3. Вычислите концентрацию дисперсной фазы золя в граммах на литр.
28. Водный раствор белка концентрацией 10 г/л при температуре 298К имеет осмотическое давление 18,57 мм рт. ст. Вычислите молекулярную массу белка.
29. Осмотическое давление раствора каучука в бензоле равно 405,3 Н/м2 при 27°С. Концентрация раствора равна 1 кг/м3. Вычислите молярную массу каучука.
30. Протаргол содержит 0,08% коллоидного серебра. Осмотическое давление этого коллоидного раствора равно 0,08 Па при температуре 37оС. Рассчитайте средний диаметр сферических коллоидных частиц золя. Плотность серебра 10,5∙103 кг/м3.
31. Осмотическое давление коллоидного раствора 0,1014 кг золота, диспергированного в 1м3 при 25°С, равно 98,06 Н/м2. Определите радиус частиц золя золота, предполагая, что форма частиц сферическая. Плотность золота составляет 19,6·103 кг/м3.
32. Осмотическое давление коллоидного раствора, содержащего 2,8 кг диспергированной ртути в 1м3, при 18°С равно 3,45 Па. Определите размер частиц золя ртути: а) форма частиц сферическая – радиус частиц; б) форма частиц – кубическая – длину ребра частицы. Плотность ртути равна 13,55·103 кг/м3.
33. Гидрозоль сульфида мышьяка содержит 7,2 кг As2S3 в 1 м3 золя. Средний диаметр частиц составляет 2·10−8 м. Вычислите: а) частичную концентрацию гидрозоля и его осмотическое давление при 273 К, если плотность твердого сульфида мышьяка равна 2,8·103 кг/м3; б) частичную концентрацию гидрозоля и его осмотическое давление, предполагая, что сульфид мышьяка образует истинный раствор такой же массовой концентрации. Во сколько раз осмотическое давление гидрозоля меньше осмотического давления предполагаемого истинного раствора?
34. Вычислите скорость оседания эмульсии ртути в воде. Плотность ртути 13,6·103 кг/м3; плотность воды 1·103 кг/м3; вязкость воды 1·10−3 Па·с; диаметр капель ртути равен 1·10−6 м.
35. С какой скоростью осаждаются частицы аэрозоля хлорида аммония плотностью 1500 кг/м3, имеющие радиус 4,5∙10−7 м? Вязкость воздуха можно принять равной 1,76∙10−5 Пас, а плотностью воздуха можно пренебречь.
36. Радиусы капель водяного тумана равны: 1) r1 = 0,01 см, 2) r2 =1∙10-4 см. Вязкость воздуха×примите равной 18∙10-6Па∙с. Вычислите, с какой скоростью будут оседать капли тумана.
37. Вычислите скорость оседания золя платины в воде. Плотность платины 21,4·103 кг/м3, плотность воды 1·103 кг/м3, вязкость воды составляет 1·10−3 Па·с, радиус частиц платины равен 3·10−7 м. Во сколько раз увеличится скорость оседания частиц золя платины при увеличении радиуса частиц в 10 раз?
38. Определите скорость оседания частиц суспензии каолина в воде с радиусом частиц 2·10−6 м при 15°С, если вязкость воды при этой температуре равна 1,14·10−3 Па·с. Плотность каолина составляет 2,2·103 кг/м3, плотность воды равна 1·103 кг/м3.
39. Время оседания частиц в воде на 1см равно 16 час при 298К. Частицы имеют сферическую форму, а плотность их вещества равна 10 г/см3, плотность воды − 1,0 г/см3. Вычислите радиус частиц, если вязкость воды при 298К равна 0,894∙10−3 Па∙с.
40. Определите удельную поверхность порошка сульфата бария (м2/кг), если его частицы оседают в водной среде с высоты 0,226 м за 1350 с. Предположите, что частицы имеют сферическую форму. Плотность сульфата бария 4,5·103 кг/м3, плотность воды 1·103 кг/м3, вязкость воды 1·10−3 Па·с.
41. Рассчитайте размер частиц диоксида кремния, если известно, что время их оседания на расстояние 1см составляет: а) 30с; б) 60 мин; в) 100ч. Плотность дисперсной фазы и дисперсионной среды составляет 2700 и 1100 кг/м3 соответственно, вязкость среды 1∙10−3 Па∙с.
42. Пробирка высотой 0,1м заполнена высокодисперсной суспензией кварца (плотность 2700 кг/м3) в воде (плотность 1000кг/м3). Время полного оседания частиц равно 2ч. Каков минимальный размер частиц, если они имеют сферическую форму?
43. Определите, за какое время осядет частица бентонита, находящаяся у поверхности жидкости, если высота столба жидкости равна 0,1 м, вязкость среды − 2∙10−3 Па∙с, плотность частицы 2100 кг/м3, плотность дисперсионной среды 1000кг/м3.
44. Сферические частицы радиусом 1∙10-3, 1∙10-5, 1∙10-7 см оседают в воде на 1см под действием гравитации. Вязкость воды h = 1∙10-3 Па∙с; плотность воды равна 1∙103 кг/м3; плотность вещества частиц×r×= 10∙103 кг/м3. Вычислите теоретическое время оседания частиц.
45. Сферические частицы радиусом 1∙10-3, 1∙10-5, 1∙10-7 см оседают в воде на 1см под действием гравитации. Вязкость воды h = 1∙10-3 Па∙с; плотность воды равна 1∙103 кг/м3; плотность вещества частиц×r×= 2,7∙10 3 кг/м3. Вычислите теоретическое время оседания частиц.
46. Вычислите скорости оседания частиц радиусом 10 мкм, образующихся после помола зерен кофе в воде (h = 1×10-3 Па∙с) и в воздухе (h = 18∙10-6 Па∙с); плотность кофе равна 1,1∙103 кг/м3, воды и воздуха 1∙103 кг/м3 и 1,205 кг/м3 при 293К соответственно.
47. Характеристикой устойчивости дисперсных систем против действия силы тяжести является гипсометрическая высота, равная расстоянию между двумя горизонтальными слоями, на которой концентрация частиц золя уменьшается в 2 раза. Вычислите гипсометрическую высоту золя золота (плотность золота равна 19300 кг/м3; радиус частиц равен 4∙10−9 м) при 25°С.
48. Гидрозоль золота состоит из частиц диаметром 2·10−9 м. На какой высоте при 27°С число частиц в золе уменьшится в два раза? Плотность золота 19,6·103 кг/м3, плотность воды 1·103 кг/м3.
49. Радиус сферических частиц r×= 1∙10-8м; плотность частиц r = 1,2∙103 кг/м3; плотностью воздуха можно пренебречь, Т = 293К. Используя гипсометрическое уравнение седиментационно-диффузионного равновесия, вычислите высоту над поверхностью Земли, на которой число частиц аэрозоля угольного дыма будет уменьшаться в 2 раза.
50. Средний радиус частиц дыма r = 1∙10-8 м, плотность частиц r = 1,2∙103 кг/м3, Т = 290К, плотностью воздуха можно пренебречь. Вычислите концентрацию частиц дыма на высоте 1 м, если на исходном уровне их концентрация была 1,5∙10-3кг/м3.
51. Золь диоксида кремния воде содержит частицы, радиус которых равен 2∙10−8 м. Определите, на какой высоте концентрация частиц уменьшается в 2 раза. Плотности диоксида кремния и дисперсионной среды равны 2700 кг/м3 и 1000 кг/м3 соответственно; температура равна 298К.
52. На какой высоте от дна сосуда при 17°С концентрация гидрозоля сульфида мышьяка уменьшится втрое, если средний диаметр частиц 1·10−8 м? Плотность сульфида мышьяка 1,9·103 кг/м3, плотность воды 0,999·103 кг/м3.
53. Определите радиус частиц гидрозоля золота, если после установления диффузионно-седиментационного равновесия при 293К на высоте 8,56 см, концентрация частиц уменьшается в е раз. Плотность золота равна 19,3 г/см3, плотность воды − 1,0г/см3.
54. Число сферических частиц гидрозоля золота, находящегося в равновесии в поле силы тяжести, равно 386. Чему равно число частиц в слое, лежащем на 1·10−4 м выше, если средний диаметр частиц равен 6,6·10−8 м? Температура 19°С; плотность золота равна 19,6·103 кг/м3; плотность воды составляет 0,998·103 кг/м3.
55. При подсчете числа частиц гидрозоля селена на двух уровнях, находящихся друг от друга на расстоянии 1·10−4 м, на нижнем уровне оказалось 733 частицы, на верхнем 444 частицы. Температура 19°С; плотность селена равна 4,27·103 кг/м3, плотность воды равна 0,998·103 кг/м3. Вычислите средний радиус частиц селена, приняв их форму сферической.
Видео:ЕГЭ по математике // Задание 5, 7 // Иррациональное уравнениеСкачать
III. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ И СТРУКТУРНО-МЕХАНИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ
Пример 1
Определите коэффициент диффузии D и среднеквадратичный сдвиг 
частицы гидрозоля за время τ = 10 с, если радиус частицы r = 50 нм, температура Т=293,2 К, вязкость среды η = 10 -3 Па*с.
Решение. Коэффициент диффузии рассчитывается по уравнению Эйнштейна:
Коэффициент диффузии и средний сдвиг частицы связаны уравнением Эйнштейна-Смолуховского: 
, тогда среднеквадратичный сдвиг частицы составит: 
Пример 2
Определите радиус гидрозоля золота, если после установления диффузионно- седиментационного равновесия при 293 К на высоте h = 8,5 см концентрация частиц изменяется в е раз. Плотность золота ρ = 19,3 г/см 3 , плотность воды ρ = 1,0 г/см 3 .
Решение. При установлении диффузионно-седиментационного равновесия распределение частиц по высоте рассчитывается по уравнению гипсометрического закона:
сh, с0 — концентрация гидрозоля на высоте и начальная, соответственно.
— объем частицы, для сферических частиц равен 
Согласно условию задачи сh = c/е, тогда 
. С учетом этого выражение для радиуса частиц принимает вид:
Пример 3
Рассчитайте осмотическое давление 30%-ного гидрозоля SiO2 при температуре 293,2 К, если удельная поверхность частиц Sуд=2,7*10 5 м 2 /кг. Плотность частиц гидрозоля SiO2 ρ=2,2 г/см 3 , плотность среды ρ=1,15 г/см 3 .
Решение. Для дисперсных систем осмотическое давление π рассчитывается по уравнению Вант-Гоффа следующего вида:
с- массовая концентрация частиц;
m- масса одной частицы.
Находим массовую концентрацию частицы дисперсной фазы:
Массу сферической частицы определяем по формуле 
, диаметр частицы 
. Тогда 
кг.
Рассчитываем осмотическое давление:
Пример 4
Какое центробежное ускорение должна иметь центрифуга, чтобы вызвать оседание частиц радиусом r равным 5 . 10 -8 м и плотностью ρ=3. 10 3 кг/м 3 в среде с плотностью ρ0=1 . 10 3 кг/м 3 и вязкостью η=1 . 10 -3 Па . с при температуре 300 К.
Решение. Для того, чтобы происходило оседание частиц, необходимо преобладание скорости оседания над скоростью теплового движения примерно на порядок. Для оценки скорости теплового движения частиц рассчитывают средний сдвиг 
за 1 с, по уравнению:
Задаемся скоростью оседания Uц=3 . 10 -5 м/с. По уравнению
находим центробежное ускорение
Пример 5
Рассчитайте толщину диффузионного ионного слоя λ на поверхности частиц сульфата бария, находящихся в водном растворе хлорида натрия с концентрацией 25 мг/дм 3 . Относительная диэлектрическая проницаемость раствора при 288 К равна ε=82,2.
Решение. Толщина диффузионного ионного слоя рассчитывается по уравнению: 
, где
ε0= 8,85 . 10 -12 Ф/м электрическая постоянная,
F=96500 Кл/моль постоянная Фарадея,
ионная сила раствора (с-концентрация моль/м 3 ).
Для электролита NaCl ионная сила равна: 
.
Выразим концентрацию раствора NaCl в моль/м 3 :
Следовательно, I=0,428. Рассчитаем толщину λ:
Пример 6
Рассчитать и сравнить время оседания частиц в гравитационном и центробежном полях при следующих условиях: радиус частиц r=10 -7 м; плотность дисперсной фазы ρ=3 . 10 3 кг/м 3 ; плотность дисперсионной среды ρ0=1 . 10 3 кг/м 3 ; вязкость η=1 . 10 -3 Па . с; высота оседания H=0,1 м; центробежное ускорение ω 2 h= 200g
Решение. Время оседания 
. Скорость оседания частиц в гравитационном поле рассчитывают по уравнению:
Следовательно: 
Пример 7
Рассчитать радиус частиц золя AgCl в воде, если время оседания в центрифуге составило 10 мин при следующих условиях: исходный уровень h1=0,09 м; конечный уровень h2=0,14 м; плотность дисперсной фазы ρ=5,6 . 10 3 кг/м 3 ; плотность дисперсионной среды ρ0=1 . 10 3 кг/м 3 ; частота вращения центрифуги u=1000 об/мин; вязкость η=1 . 10 -3 Па . с.
Решение. Радиус частиц рассчитывают по уравнению:
Угловая скорость ω=2πn/60, где n— число оборотов в минуту (частота вращения). Следовательно, 
ЛИТЕРАТУРА
1. Щукин Е.Д. Коллоидная химия / Е.Д. Щукин, А.В. Перцев, Е.А. Амелина. — М.: Изд-во МГУ, 2004.
2. Зимон А.Д. Коллоидная химия: учебник для вузов / А.Д. Зимон, Н.Ф. Лещенко. — М.: АГАР, 2001.
3. Гельфман М.И. Коллоидная химия / М.И. Гельфман, О.В. Ковалевич, В.П. Юстратов. — СПб.: Лань, 2003.
4. Лабораторные работы и задачи по коллоидной химии / Под ред. Ю.Г. Фролова и А.С. Гродского — М.: Химия,1986.
💥 Видео
9 класс, 6 урок, Уравнение окружностиСкачать
Согласованные и несогласованные определенияСкачать
Лекция №14. Полярное разложение. Квадратичные формы в евклидовом пространствеСкачать
Задача 6 №27827 ЕГЭ по математике. Урок 96Скачать
#4warmup. Разбор четвертой разминкиСкачать
Задача 12 Профильный ЕГЭ. Сложные уравнения. Сироп 2.0 математикаСкачать
Сопротивление материалов. Занятие 10. Часть 1. Расчет статически неопределимой балки.Скачать
Определение формулы органических соединений. 1 часть. Практическая часть - решение задачи. 9 класс.Скачать
Cумма ряда 1/n^2. Базельская проблема: решение через разложения в ряд Фурье.Скачать
Расстановка коэффициентов методом электронного баланса | Химия TutorOnlineСкачать
Ягола А. Г. - Вариационное исчисление - Понятие функционалаСкачать
РУССКИЙ ЯЗЫК 8 класс: Согласованные и несогласованные определенияСкачать
Геометрия и группы. Алексей Савватеев. Лекция 5.1. Факторизация на примере целых чиселСкачать
Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать
Разложение нитратов за 5 минут | ХИМИЯ ЕГЭ | СОТКАСкачать
Кривая. Замкнутые и незамкнутые линии. Математика 1класс.Скачать
Фазовые кривые.Скачать
Двухфазное КЗ на векторных диаграммахСкачать
