Курсовая работа численные методы. РЕШЕНИЕ УРАВНЕНИЙ И ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
Кафедра «Автоматика и системы управления»
РЕШЕНИЕ УРАВНЕНИЙ И ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ
Пояснительная записка к курсовому проекту
по дисциплине «Численные методы»
Студентка гр. ИС 20253
Руководитель –доцент кафедры АиСУ
____________А. C. Окишев
Пояснительная записка содержит 30 страниц, 18 рисунков, 5 таблиц, 3 источника.
Численный метод, нелинейное уравнение, корень, итерация, сходимость, аппроксимация, интерполяция, многочлен Лагранжа, задача Коши, погрешность, кубический сплайн, обыкновенное дифференциальное уравнение.
Объектом исследования являются приближенные численные методы решения некоторых математических и инженерных задач, а также программное обеспечение, реализующее эти методы.
Цель работы – ознакомиться с численными методами решения нелинейных и дифференциальных уравнений и интерполяции функций, решить предложенные типовые задачи с помощью предоставленного преподавателем программного обеспечения, сформулировать выводы по полученным решениям, отметить достоинства и недостатки методов, сравнить удобство использования и эффективность работы каждой программы.
Пояснительная записка к курсовому проекту оформлена в текстовом редакторе MicrosoftOffice 2010 с установленным интерактивным редактором формул MathType 6.6. Графики нелинейных функций построены с помощью программы AdvancedGrapher. При решении обыкновенных дифференциальных уравнений использовалась среда математического моделирования Mathcad 14.
В связи с развитием новой вычислительной техники инженерная практика наших дней все чаще и чаще встречается с математическими задачами, точное решение которых получить весьма сложно или невозможно. В этих случаях обычно прибегают к тем или иным приближенным вычислениям. Вот почему приближенные и численные методы математического анализа получили за последние годы широкое развитие и приобрели исключительно важное значение.
Новые вычислительные средства вызвали переоценку известных методов решения задач с точки зрения целесообразности их реализации на ЭВМ и стимулировали создание более эффективных, что привело к появлению новой дисциплины – вычислительной математики. Предметом изучения последней являются численные методы решения задач математического анализа: изучение алгоритмов и условий сходимости итерационных методов, определение границ применимости методов, исследования оценок погрешностей методов и вычислений. Главным разделом вычислительной математики является реализация численных методов на ЭВМ, то есть составление программы для требуемого алгоритма и решения с ее помощью конкретной задачи.
Любая прикладная задача формируется исходя из определенного физического смысла некоторого процесса (распределение тепла в стержне, описание траектории движения объектов). Прикладная математическая задача может быть сформулирована, например, из описания некоторой экономической модели (задача распределения ресурсов, задача планирования производства, транспортная задача перевозки грузов, оптимальных в заданном смысле). Следовательно, для постановки любой прикладной задачи нужна математическая модель. Поэтому, можно выделить следующие этапы решения задач на ЭВМ:
1) описание математической модели задачи на основе физической или экономической модели;
2) изучение методов решения поставленной математической модели задачи и создание новых методов;
3) выбор метода решения задачи исходя из заданной точности решения и особенностей задачи;
4) составление блок-схемы программы для решения задачи на ЭВМ;
5) отладка программы и оценка полученных результатов;
6) решение задачи на ЭВМ, построение графиков, получение оценки погрешностей, обоснование результатов.
В курсовом проекте рассматриваются не прикладные, а типовые математические задачи, которые могут возникнуть при переходе от реальных систем к их математическим моделям, поэтому основное внимание уделяется последнему этапу.
1 Решение нелинейных уравнений
Нелинейными уравнениями называются уравнения вида
где – нелинейная функция, которая может относиться к трем типам:
1) нелинейная алгебраическая функция вида
2) трансцендентные функции – тригонометрические, обратные тригонометрические, логарифмические, показательные и гиперболические функции;
3) различные комбинации этих функций, например, .
Решением нелинейного уравнения является такая точка , которая при подстановке в уравнение обращает его в тождество. На практике не всегда удается подобрать такое решение. В этом случае решение уравнения находят с применением приближенных (численных) методов. Тогда решением будет являться такая точка , при подстановке которой в уравнение последнее будет выполняться с определенной степенью точности, т.е. , где e – малая величина. Нахождение таких решений и составляет основу численных методов и вычислительной математики.
Решение нелинейных уравнений разделяется на два этапа: отделение корней уравнений и уточнение корней нелинейных уравнений.
На первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то узнать, сколько их, и затем определить интервалы, в каждом из которых находится единственный корень.
Первый способ отделения корней – графический. Исходя из уравнения , можно построить график функции . Тогда точка пересечения графика с осью абсцисс является приближенным значением корня. Если f(x) имеет сложный вид, то ее можно представить в виде разности двух функций . Так как , то выполняется равенство .Если построить два графика , , то абсцисса точки их пересечения будет приближенным значением корня уравнения.
Второй способ отделения корней нелинейных уравнений – аналитический. Он основывается на следующих трех теоремах.
Теорема 1. Если функция непрерывна на отрезке и меняет на концах отрезка знак (т.е. ), то на содержится хотя бы один корень.
Теорема 2. Если функция непрерывна на отрезке , выполняется условие вида и производная сохраняет знак на , то на отрезке имеется единственный корень.
Теорема 3. Если функция является многочленом n-ой степени и на концах отрезка меняет знак, то на имеется нечетное количество корней (если производная сохраняет знак на , то корень единственный). Если на концах отрезка функция не меняет знак, то уравнение либо не имеет корней на , либо имеет четное количество корней.
При аналитическом методе исследований необходимо выявить интервалы монотонности функции . Для этого необходимо вычислить критические точки , в которых первая производная равна нулю или не существует. Тогда вся числовая ось разбивается на интервалы монотонности . На каждом из них определяется знак производной , где . Затем выделяются те интервалы монотонности, на которых функция меняет знак.
На втором этапе на каждом из этих интервалов для поиска корня используются численные итерационные методы уточнения корней, например методы половинного деления, простых итераций или Ньютона.
1.1 Метод простых итераций
Пусть известно, что нелинейное уравнение имеет на отрезке единственный вещественный корень . Требуется найти этот корень с заданной точностью. Применяя тождественные преобразования, приведем уравнение к виду
Выберем произвольно приближенное значение корня и вычислим . Найденное значение подставим в правую часть соотношения (2) и вычислим . Продолжая процесс вычислений дальше, получим числовую последовательность . Если существует предел этой последовательности, то он и является корнем уравнения . В самом деле, пусть . Тогда, переходя к пределу в равенстве
и учитывая непрерывность функции на отрезке , получим
Корень можно вычислить с заданной точностью по итерационной формуле
Достаточное условие, при котором итерационный процесс сходится, определяет следующая теорема: пусть функция определена и дифференцируема на отрезке , причем все ее значения и выполняется условие
тогда процесс итераций сходится независимо от начального значения и предельное значение является единственным корнем уравнения на .
Геометрическая интерпретация метода простых итераций заключается в следующем: если построить два графика функций и , то абсцисса точки их пересечения будет корнем . Построим итерационный процесс. Зададим .Вычислим – первое приближение и – второе приближение. В первом случае (рисунок 1, а) процесс сходящийся ( ), во втором (рисунок 1, б) – расходящийся ( ).
Рисунок 1 – Сходящийся (а) и расходящийся (б) итерационные процессы
Часто, если итерационный процесс расходится из-за невыполнения условия , нелинейное уравнение можно привести к виду, допускающему сходящиеся итерации.
Выполнения условия сходимости можно добиться путем перехода от исходного уравнения к эквивалентному виду следующим образом: сначала умножить обе части уравнения (1) на , а затем прибавить к обеим частямx, тогда . Обозначив ,получим уравнение . Константа с выбирается так, чтобы выполнялось достаточное условие сходимости итерационного процесса , т.е.
Условие равносильно двойному неравенству
Поэтому константа выбирается из соотношений:
Метод простых итераций и почти все другие итерационные методы имеют два достоинства:
1) являются универсальными и самоисправляющимися, то есть любая неточность на каком-либо шаге итераций отражается не на конечном результате, а лишь на количестве итераций. Подобные ошибки устойчивы даже по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости;
2) позволяют достигнуть любой заданной точности при любом начальном приближении .
– трудность приведения уравнения к виду .
– если начальное приближение находится далеко от корня, то число итераций при этом увеличивается, а объем вычислений возрастает.
Процесс итераций заканчивается при выполнении двух критериев:
1) Когда два последних приближения отличается между собой по модулю на заданную величинуe:
Одного критерия недостаточно, так как в случае крутизны графика, данное условие будет выполнено, но может находиться далеко от корня;
2) Когда последнее вычисленное приближение к корню удовлетворяет уравнению с заданной точностью:
Отдельно критерия бывает недостаточно, так как при пологой функции условие может быть выполнено, но может быть далеко от корня.
1.2 Метод Ньютона
Пусть уравнение имеет на интервале единственный корень, причем существует непрерывная на производная . Метод Ньютона служит для уточнения корней нелинейных уравнений в заданном интервале. Его можно рассматривать как частный случай метода простых итераций, если
Тогда итерационный процесс осуществляется по формуле:
Геометрически этот процесс представлен на рисунке 2. Он означает замену на каждой итерацииk графика кривой касательной к ней в точках с координатами .
Достаточное условие сходимости обеспечивается выбором начальной точки . Начальным приближением служит один из концов отрезка , в зависимости от того, в каком из них выполняется достаточное условие сходимости
При произвольном начальном приближении итерации сходятся, если
Метод Ньютона рекомендуется применять для нахождения простых действительных корней уравнения .
Достоинством метода является то, что он обладает скоростью сходимости, близкой к квадратичной.
– не при любом начальном приближении метод Ньютона сходится, а лишь при таком, для которого ;
– если , т.е. касательная к графику почти параллельна оси абсцисс, то и метод расходится;
– если ,т.е. касательная к графику почти параллельна оси ординат, то и продвижения к корню не будет.
Последних трудностей можно избежать, применив модификацию метода Ньютона, в которой используется только касательная в точке начального приближения. Рабочая формула при этом имеет вид:
1.3 Решение нелинейного уравнения методом простых итераций
Решите нелинейное уравнение
методом простой итерации:
- a) выполните приблизительную оценку корней предложенного уравнения с помощью системы MathCad, графической программы AdvancedGrapher или вручную;
б) преобразуйте уравнение вида f (x) = 0 к итерационному виду x = φ(x), гарантировав при этом сходимость метода простой итерации;
в) с помощью программы MeProst уточните один из корней первого уравнения вида f (x)=0 с точностью ε = 10 -3 , выбрав подходящий отрезок для построения графической иллюстрации работы метода простой итерации;
г) в пояснительной записке приведите график функции f (x) с указанием выбранных для уточнения корней, результаты уточнения корней программой MeProst, значения корней, требуемое число итераций, погрешность решения и графические иллюстрации процесса сходимости к корню.
Для приблизительной оценки корней нелинейного уравнения построим график функции с помощью программы AdvancedGrapher (рисунок 3).
Из рисунка 3 видно, что график функции пересекает ось абсцисс в одной точке, поэтому уравнение имеет один корень.
т.е. для уточнения корня будем использовать итерационную последовательность:
где – номер итерации.
С помощью программы MeProst выполним уточнение корня. В разделе меню «Ввод» задаем следующие параметры (Рисунок 4):
Рисунок 4 –Ввод параметров в программе Newton
- отрезок, на котором находится уточняемый корень ;
- необходимая точность приближения к корню ;
- начальное приближение к корню
- максимальное допустимое число итераций .
Чтобы получить наглядное представление о процессе сходимости к корню, выберем пошаговый режим расчета. В открывшемся окне (рисунок 5) видим графики функций (зеленый) и (красный). Очевидно, что корень уравнения определяется как точка пересечения этих двух графиков. Точка начального приближения показана синим цветом. Чтобы вычислить следующее приближение геометрическим способом, необходимо найти точку пересечения прямой и кривой и ординату этой точки взять в качестве . Последующие приближения определяются аналогично.
Рисунок 5 – Метод простых итераций
Как следует из рисунка 5, итерационный процесс сходится (с каждый новым шагом мы приближаемся к решению).
Корнем данного уравнения является
1.4 Решение нелинейного уравнения методом Ньютона
Решите нелинейное уравнение
- a) выполните приблизительную оценку корней уравнения с помощью системы MathCad, графической программы AdvancedGrapher или вручную;
б) с помощью программы Newton уточните один из корней первого уравнения вида f (x)=0 с точностью ε = 10 -3 , выбрав подходящий отрезок для построения графической иллюстрации работы метода Ньютона;
в) в пояснительной записке приведите график функции f(x) с указанием выбранных для уточнения корней, результаты уточнения корней программой Newton, значения корней, требуемое число итераций, погрешность решения и графические иллюстрации процесса сходимости к корню.
Для приблизительной оценки корней нелинейного уравнения построим график функции с помощью программы AdvancedGrapher (рисунок 6).
Как видно из рисунка 6, график функции пересекает ось абсцисс в двух точках, поэтому первый корень x 1 = -2, второй корень x 2 = 5,5.
С помощью программы Newton выполним уточнение выбранного корня. Для этого в разделе меню «Ввод» задаем следующие параметры (рисунок 7):
- отрезок построения касательных к графику функции ;
- необходимая точность приближения к корню ;
- начальное приближение к корню ;
- максимальное допустимое число итераций .
Рисунок 7 – Ввод параметров в программе Newton
Рисунок 8 – Четвертая итерация метода Ньютона
Как видно из рисунка 8, корень уравнения 5 найден с заданной точностью за итераций, погрешность решения составляет .
2 Интерполяция функций
Задача интерполяции функций возникает в тех случаях, когда:
функция задана в виде таблицы, и необходимо знать значения функции для промежуточных значений аргументов, расположенных в таблице между узлами , а также для аргументов, расположенных вне таблицы;
известна лишь таблица функции и требуется определить ее аналитическое выражение;
известно аналитическое выражение функции, но оно имеет очень сложный вид, вследствие чего возникает необходимость представления этой функции в более простом виде. Например, при вычислении определенных интегралов вида можно заменить подынтегральную функцию некоторой приближенной функцией в виде многочлена. Тогда
Построив интерполяционный многочлен любого вида, также можно расширить таблицу как влево, так и вправо, вычисляя построенный многочлен в точках, не принадлежащих таблице (задача экстраполяции). Кроме того, построив интерполяционный многочлен, можно уплотнить таблицу, определяя значения функции для промежуточных аргументов между узловыми точками.
2.1 Интерполяционная формула Лагранжа
Пусть задана система точек , в которых известны значения функции (см. таблицу 1).
Таблица 1 – Экспериментальные значения функции
Установим зависимость одного ряда чисел от другого и построим новую функцию, которая с определенной степенью точности будет приближена к заданной.
Рассмотрим пример построения интерполяционного многочлена Лагранжа по заданной системе точек (в общем случае для неравноотстоящих аргументов). Построим некоторый многочлен таким образом, чтобы его значения совпали со значениями функции, заданными в таблице, для тех же аргументов, то есть . Лагранж предложил строить многочлен степени nв виде:
Здесь в каждом слагаемом коэффициенту ai соответствует разность .Найдем неизвестные коэффициенты , называемые коэффициентами Лагранжа, используя условие :
Следовательно, коэффициент a0 вычисляется по следующей формуле:
Следовательно, коэффициент a1 вычисляется по формуле:
Значения остальных коэффициентов вычисляются аналогично.
С учетом найденных коэффициентов интерполяционный многочлен Лагранжа запишется в виде
Погрешность формулы определяется остаточным членом:
где x–точка наименьшего промежутка, содержащего все узлы и точкуx.
2.2 Интерполяционные формулы Ньютона
Если таблица, для которой построена формула Лагранжа, задана для равноотстоящих узлов , то формула Лагранжа упрощается.
С учетом введенных обозначений формула Лагранжа запишется в виде:
Запишем формулу Лагранжа в случае, если :
Получили формулу линейной интерполяции вида:
где – табличные разности первого порядка.
При получаем формулу квадратичной интерполяции вида:
где – табличные разности второго порядка.
Таким образом, первая интерполяционная формула Ньютона будет иметь вид:
Остаточный член формулы имеет вид:
где ,x – точка наименьшего промежутка, содержащего все узлы и точкуx.
Первая интерполяционная формула рекомендуется для интерполяции в начале таблицы.
Вторая интерполяционная формула Ньютона используется при вычислении функции для значений , близких к концу таблицы и для продолжения таблицы. Обозначим через , тогда
Тогда получим следующую формулу Ньютона:
имеет тот же смысл, что и в первой формуле Ньютона.
2.3 Интерполяция кубическими сплайнами
Кубическим сплайном называется функция , которая:
- на каждом отрезке является многочленом третьей степени;
- имеет непрерывные первую и вторую производные на всем отрезке [a, b];
- в точках xi выполняются равенства и ;
- имеет граничные условия вида .
По количеству точек, учитываемых при аппроксимации функции, кубические сплайны можно разделить на локальные и глобальные.
Локальные сплайны используют производные , вычисляемые по трем заданным точкам, ближайшим к точке x, в которой необходимо вычислить значение функции.
Глобальные сплайны используют массив вторых производных по всем узловым точкам , который рассчитывается заранее путем решения системы линейных алгебраических уравнений (СЛАУ).
Пусть имеется таблица значений , где i изменяется от 0 до n.
Получается n+1 узел, причем сетка узлов неравномерная, тогда на интервале для нахождения значения сплайна в некоторой введенной точке необходимо проверить, принадлежит ли данная точка интервалу значений исходной таблицы.
- Если принадлежит, то формула вычисления значения сплайна в точке имеет вид:
где – расстояние между соседними узлами;
– значения функции в узловых точках;
– значения вторых производных.
Вторые производные mi находятся из трехдиагональной СЛАУ:
Всего в системе n–1 уравнение и n+1 неизвестная: . Система не полностью определяет mi. Сводим ее к трехдиагональной СЛАУ заданием граничных условий. Для нормального сплайна , . Теперь в СЛАУ n–1неизвестная иона является трехдиагональной. Такая система решается методом прогонки.
- Асимптотическое поведение сплайна вне интервала описывается формулами:
- линейная экстраполяция при (влево):
- линейная экстраполяция при (вправо):
2.4 Интерполяция функций сплайнами по таблице значений
Постройте график кубического сплайна и вычислите значения неизвестной функции f(x) в промежуточных точках.
Для каждого из двух предложенных наборов экспериментальных данных (см. таблицу 2):
а) с помощью программы Splacc постройте график кубического нормального сплайна и приведите его в пояснительной записке;
б) с помощью программы Splacc вычислите значения неизвестной функции f(x) во всех предложенных промежуточных точках;
в) вычислите те же значения неизвестной функции f(x) в промежуточных точках, введя их единым массивом в программе Spladd;
г) сравните программы Splacc и Spladd, укажите достоинства и недостатки каждой из них, а также отличия в полученных числовых значениях, если таковые имеются.
Таблица 2 – Экспериментальные данные для кубической интерполяции
Графики сплайнов для первой и второй функции, построенные с помощью программы Splacc, представлены на рисунке10.
Рисунок 10 – Интерполяция сплайном для первой (а) и второй (б) функции в программе Splacc
Значения сплайна в расчетных точках приведены в таблицах 3,4. Расчеты значений сплайнов программами Splacc и Spladd дали одинаковые результаты.
Таблица 3 – Значения сплайна в расчетных точках в программе Splacc
Рисунок 11 – Значения сплайна в расчетных точках в программе Spladd для первой (А) и второй функции (Б)
3 Решение обыкновенных дифференциальных уравнений
Дифференциальные уравнения являются основным математическим инструментом моделирования и анализа разнообразных явлений и процессов в науке и технике.
Методы их решения подразделяются на два класса:
аналитические методы, в которых решение получается в виде аналитических функций;
численные (приближенные) методы, где искомые интегральные кривые получают в виде таблиц их численных значений.
Применение аналитических методов позволяет исследовать полученные решения методами математического анализа и сделать соответствующие выводы о свойствах моделируемого явления или процесса. К сожалению, с помощью таких методов можно решать достаточно ограниченный круг реальных задач. Численные методы позволяют получить с определенной точностью приближенное решение практически любой задачи.
Решить дифференциальное уравнение
численным методом означает, что для заданной последовательности аргументов и числа , не определяя аналитического вида функции , найти значения , удовлетворяющие начальным условиям:
3.1 Метод Эйлера.
Этот метод является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других численных методов.
Пусть дано обыкновенное дифференциальное уравнение (ОДУ) с начальными условиями (задача Коши):
и удовлетворяются условия существования и единственности решения.
Требуется найти решение задачи Коши на отрезке . Найдем решение в виде таблицы . Для этого разобьем отрезок наn равных частей и построим последовательность
где – шаг интегрирования.
Проинтегрируем исходное уравнение на отрезке :
Полученное соотношение можно переписать как
Если считать подынтегральную функцию постоянной на участке и равной значению в начальной точке этого интервала , то получим
Подставляя полученный результат в формулу , получим основную расчетную формулу метода Эйлера:
Вычисление значений осуществляется с использованием формулы следующим образом. По заданным начальным условиям иy0, полагая в выражении , вычисляется значение
Далее, определяя значение аргумента x по формуле , используя найденное значение y1 и полагая в формуле , вычисляем следующее приближенное значение интегральной кривой как
Поступая аналогичным образом при , определяем все остальные значенияyk, в том числе последнее значение
которое соответствует значению аргумента .
Таким образом, соединяя на координатной плоскости точки отрезками прямых в качестве приближенного представления искомой интегральной кривой , получаем ломанную линию с вершинами в точках .
Метод Эйлера может быть применен к решению систем дифференциальных уравнений.
Пусть задана система двух уравнений первого порядка:
с начальными условиями
Необходимо найти решение этой задачи Коши. Проводя аналогичные рассуждения, получаем расчетные формулы вида:
гдеh– шаг интегрирования.
При расчетах полагается, что и . В результате применения расчетной схемы получается приближенное представление интегральных кривых и в форме двух ломанных Эйлера, построенных по полученным таблицам . Точность метода Эйлера .
3.2 Решение ОДУ методом Эйлера
Решите ОДУ первого порядка (задачу Коши)
а) изучите устройство и работу шаблона МЭ в среде математического моделирования MathCAD и получите методом Эйлера таблицу значений неизвестной функции y(x);
б) аппроксимируйте полученные данные кубическим сплайном и постройте приближенный график функции y(x) в программе Splacc.
Вводим исходные данные в шаблон МЭ.mcd и по формуле определяем значение y1(листинг 1).
Листинг 1 – Первый шаг метода Эйлера
Подставляя найденное значение y1 в формулу, вычисляем следующее значение функции y2 (листинг 2).
Листинг 2 – Второй шаг метода Эйлера
Остальные значения функции вычисляются аналогично до тех пор, пока не будет достигнут правый конец отрезка интегрирования (листинг 3).
Листинг 3 – Последний шаг метода Эйлера
Полученные значения неизвестной функции представлены в таблице 4.
Таблица 4 – Значения функции
Аппроксимируем таблично заданную функцию кубическим сплайном с помощью программы Splacc. График сплайна показан на рисунке 15. Как видно из рисунка, решение ОДУ практически линейно.
Рисунок 15 – Интерполяция численного решения ОДУ кубическим сплайном
3.3 Решение ОДУ методом Эйлера-Коши
Решите ОДУ первого порядка (задачу Коши)
а) изучите устройство и работу шаблона МЭК в среде математического моделирования MathCAD и получите методом Эйлера-Коши таблицу значений неизвестной функции y(x);
б) аппроксимируйте полученные данные многочленом Лагранжа и постройте приближенный график функции y(x) в программе Lagr;
Вводим исходные данные в шаблон МЭК.mcd и определяем значение y1 (листинг 4).
Листинг 4 – Первый шаг метода Эйлера-Коши
Остальные значения функции вычисляются аналогично по шаблону МЭК до тех пор, пока не будет достигнут правый конец отрезка интегрирования (листинг 5).
Листинг 5 – Последний шаг метода Эйлера-Коши
Полученные значения неизвестной функции представлены в таблице 5.
Таблица 5 – Значения функции
Аппроксимируем таблично заданную функцию многочленом Лагранжа с помощью программы Lagr. График многочлена приведен на рисунке 18. Как следует из рисунка, в данном случае решение ОДУ имеет нелинейный характер.
Рисунок 18 – Интерполяция численного решения ОДУ многочленом Лагранжа
Недостаток аналитических методов – использование целого ряда допущений и предположений в процессе построения математических моделей и невозможность, в некоторых случаях, получить решение в явном виде из-за неразрешимости уравнений в аналитической форме, отсутствия первообразных для подынтегральных функций и т.п. В этих случаях широко применяются численные методы.
Численные методы основываются на построении конечной последовательности действий над числами. Применение численных методов сводится к замене математических операций и отношений соответствующими операциями над числами, например, к замене интегралов суммами, бесконечных сумм – конечными и т.п. Результатом применения численных методов являются таблицы и графики зависимостей, раскрывающих свойства объекта. Численные методы являются продолжением аналитических методов в тех случаях, когда результат не может быть получен в явном виде. Численные методы по сравнению с аналитическими методами позволяют решать значительно более широкий круг задач.
Предложенные преподавателем программы показали себя эффективно для решения конкретных задач, под которые они были написаны. Но их использование для решения различных инженерных задач нецелесообразно из-за крайне ограниченного функционала. Возможный выход – это самостоятельное написание программ под конкретные задачи, но это чревато большими трудозатрами. Альтернатива – использование коммерческих пакетов (например, системы математического моделирования Mathcad, Matlab, Maple и т.д.), позволяющих решать очень широкий круг задач. Использование различных скриптов к этим коммерческим пакетам также позволяет еще сильнее расширить их функционал.
Примеров инженерных задач, в которых могут потребоваться изученные численные методы, можно привести целое множество. Прежде всего это те направления, где требуется математическое моделирование различных процессов. Например, моделирование уличной дорожной сети (для оптимизации использования общественного и частного транспорта), моделирование использования различных инженерных сооружений для расчета эффективности их использования и расчета оптимальных, а также максимальных нагрузок на них, моделирование взаимодействия инженерных сооружений и окружающей среды для расчета возможных экологических последствий их использования.
- ВержбицкийВ.М. Численные методы. Линейная алгебра и нелинейные уравнения. М.: Оникс 21 век, 2005. – 636 с.
- ВержбицкийВ.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Оникс 21 век, 2005. – 400 с.
- Бахвалов Н.С. Численные методы/ Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков – М.: Бином. Лаборатория знаний, 2008. – 432 с.
Скачать: У вас нет доступа к скачиванию файлов с нашего сервера. КАК ТУТ СКАЧИВАТЬ
Видео:Математика это не ИсламСкачать

Преимущества и недостатки численного решения
Преимущества численного решения. Перечислим преимущества численного решения по сравнению с соответствующим экспериментальным исследованием.
Низкая стоимость. Наиболее важным преимуществом численного решения является его небольшая стоимость. В большинстве случаев стоимость затраченного машинного времени на много порядков ниже стоимости соответствующего экспериментального исследования. Значение этого фактора возрастает с увеличением масштабов и усложнением требующего изучения физического процесса.
Скорость. Численное исследование можно провести очень быстро. Конструктор имеет возможность меньше, чем за день, просчитать сотни вариантов и выбрать оптимальную конструкцию, в то время как соответствующее экспериментальное исследование заняло бы очень много времени.
Полнота информации. Численное решение задачи дает подробную и полную информацию. С его помощью можно найти значения всех имеющихся переменных (таких, как скорость, давление, температура, концентрация, интенсивность турбулентности) во всей области решения. В отличие от эксперимента для расчета доступна практически вся исследуемая область и отсутствуют возмущения процесса, вносимые датчиками при экспериментальном исследовании. Очевидно, что ни в одном экспериментальном исследовании невозможно измерить распределения всех переменных во всей исследуемой области. Поэтому, даже если проводится экспериментальное исследование, большое значение для дополнения экспериментальной информации имеют результаты численного решения.
Возможность математического моделирования реальных условий. Численное решение можно получить для реальных условий исследуемого процесса, что далеко не всегда возможно при экспериментальном исследовании.
Возможность моделирования идеальных условий. Если с помощью численного решения изучаются закономерности физического процесса, а не сложные инженерные задачи, можно сконцентрировать внимание на нескольких существенных параметрах этого процесса и исключить все несущественные явления. При этом можно моделировать многие идеализированные условия, например двумерность, постоянство плотности, адиабатическую поверхность или бесконечно быструю реакцию. При экспериментальном исследовании даже с помощью довольно тщательного эксперимента не всегда можно достичь таких идеализированных условий.
Недостатки численного решения. Численное решение дает количественное выражение закономерностей, присущих математической модели. Напротив, с помощью экспериментального исследования наблюдается сама действительность. Таким образом, полезность расчета ограничена обоснованностью математической модели. Тем не менее следует заметить, что результат численного решения зависит как от численного метода, так и от математической модели. Если используемая математическая модель не соответствует изучаемому явлению, то с помощью даже очень хорошей численной методики можно получить не нужные результаты.
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Сравнительный анализ численных методов
| Доступные действия |
|
|
Министерство образования и науки Республики Казахстан
Карагандинский государственный технический университет
по дисциплине: Математическое обеспечение САПР
Тема: Сравнительный анализ численных методов
Раздел 1 Решение нелинейных уравнений
1.2 Метод касательных
1.3 Практическое применение метода хорд для решения уравнений
1.4 Практическое применение метода касательных для решения уравнений
1.5 Программная реализация итерационных методов
Раздел 2. Решение нелинейных уравнений методом интерполирования
2.1 Многочлен Лагранжа и обратное интерполирование
2.2 Практическое применение метода интерполяции
Раздел 3. Итерационные методы решения систем линейных алгебраических уравнений
3.1 Метод простых итераций
3.2 Метод Зейделя
3.3 Практическое применение метода простых итераций при решении СЛАУ
3.4 Практическое применение метода Зейделя при решении СЛАУ
3.5 Программная реализация итерационных методов решения СЛАУ
Раздел 4.Сравнительный анализ различных методов численного дифференцирования и интегрирования
4.1 Методы численного дифференцирования
4.2 Методы численного интегрирования
Раздел 5. Численные методы решения обыкновенных дифференциальных уравнений
5.1 Метод Эйлера
5.2 Модификация метода Эйлера
5.3 Практическое применение метода Эйлера
5.4 Практическое применение уточненного метода Эйлера
Раздел 1. Решения нелинейных уравнений
Задача нахождения корней нелинейных уравнений вида F(x)=0 , где F(x)-непрерывная функция,- встречается в различных областях научных исследований. Методы решения нелинейных уравнений делятся на :
Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Такие методы применяются для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.
Однако, на практике встречаются уравнения, которые не удается решить простыми методами. Тогда используются итерационные методы решения, т. е. методы последовательных приближений.
Алгоритм нахождения корня нелинейного уравнения с помощью итерационного метода состоит из двух этапов:
а) отыскания приближенного значения корня (начального приближения);
б) уточнения приближенного значения до некоторой заданной степени точности.
В некоторых методах отыскивается не начальное приближение, а некоторый отрезок, содержащий корень, например:(метод хорд, метод касательных). Начальное приближение может быть найдено различными способами, например — графическим методом. Если оценку исходного приближения провести не удается, то находят две близко расположенные точки a и b , в которых непрерывная функция F(x) принимает значения разных знаков, т. е. F(a)>0 F(b) 0 , F(b) 0
На данном промежутке имеется только один корень.
4. Выбор точки х0 зависит от того совпадает ли её знак со знаком второй производной данной функции.
Точка а условию не удовлетворяет.
Из условия следует , что х0=b=0.35, тогда за х1 принимаем a = х1=-0.1
6. Формула для решения
При решении мы получили следующие результаты:
Условие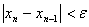
Добиться указанной точности нам удалось на 5-ой проведенной итерации.
1.4 Практическое применение метода касательных для решения уравнений
В качестве примера решим вышеупомянутое уравнение методом касательных:
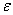
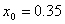
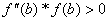
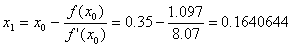
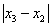
Итерационный процесс продолжается до тех пор , пока значения х1(k) , х2(k) , х3(k) не станут близкими с заданной погрешностью к значениям х1(k-1) , х2(k-1) , х3(k-1) .
Для возможности выполнения данного преобразования необходимо, чтобы диагональные элементы матрицы А были ненулевыми.
Часто систему преобразуют к виду x=x-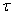
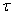
Выберем начальное приближение x0=( x01 x02… x0m)
подставляя его в праву часть системы
и вычисляя полученное выражение, находим первое приближение:
на втором шаге подставляем приближение x1 в правую часть той же системы, получим второе приближение:
Продолжая этот процесс далее, получим последовательность x1 x2 x3… xn приближений, вычисляемых по формуле :
Эта формула и выражает собой метод простой итерации.
Итерационный процесс продолжается до тех пор, пока значения х(k) не станут близкими с заданной погрешностью к значениям х(k-1).
Теорема. Метод простой итерации сходится тогда и только тогда, когда все собственные числа матрицы 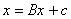
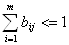
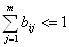
3.2 Метод Зейделя
Метод Зейделя можно использовать как модификацию метода простых итераций. Основная идея модификации состоит в том, что при вычислении очередного (k+1)-го приближения к известному xi при i>1 используют используются уже найденные приближения к известным x1,… xi-1, а не k-е приближение как в методе простых итераций.
На (k+1)-й итерации компоненты приближения 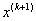
Условие сходимости метода Зейделя заключается в том, что матрица A системы Ax=b, должна удовлетворять условию:
модуль диагонального элемента должен быть больше суммы модулей оставшихся элементов строки или столбца.
Если данное условие выполнено, необходимо проследить, чтобы система была приведена к виду, удовлетворяющему решению методом простой итерации и выполнялось необходимое условие сходимости метода итераций:
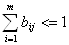
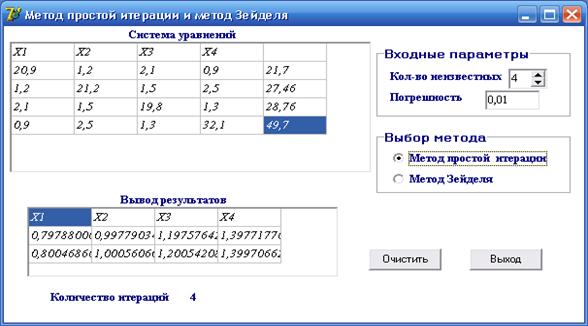
3.3 Практическое применение метода простых итераций для решения системы уравнений
Решим систему линейных уравнений методом простых итераций с точностью равной 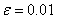
Выполним проверку на условие сходимости:
Условие выполнено, можно приступать к вычислению нулевого шага:
Начнем итерационный процесс, используя результаты начального приближения:
Проверим выполняется ли условие остановки итерационного процесса: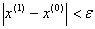
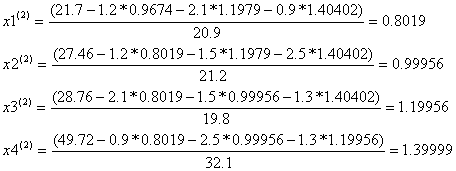
Условие остановки на первом шаге итерации не было выполнено, поэтому продолжаем итерацию, вычисляя x(2) :
Проверим выполняется ли условие остановки итерационного процесса: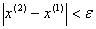
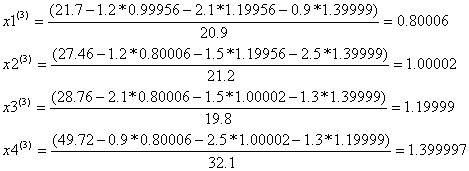
Условие остановки на втором шаге итерации не было выполнено, поэтому продолжаем итерацию, вычисляя x(3) :
Проверим выполняется ли условие остановки итерационного процесса: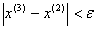
Условие остановки на третьем шаге итерации было выполнено лишь для x4, поэтому продолжаем итерацию, вычисляя x(4) :
Проверим выполняется ли условие остановки итерационного процесса:
Сходимость в сотых долях имеет место уже на 4-ом шаге, тогда можно принять
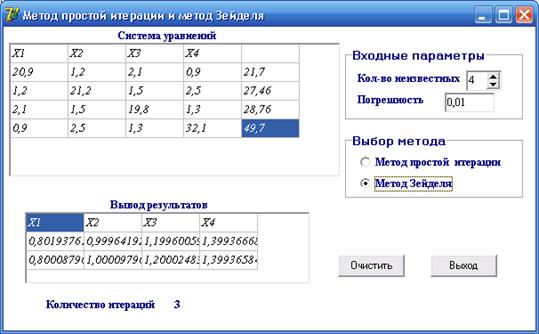
3.4 Практическое применение метода Зейделя для решения системы уравнений
Решим ту же систему линейных уравнений методом Зейделя с той же точностью : 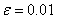
Проверку на условие сходимости мы выполнили ранее, при решении методом простых итерации.
Проверим выполняется ли условие остановки итерационного процесса:
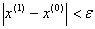
Условие остановки на первом шаге итерации не было выполнено, поэтому продолжаем итерацию, вычисляя x(2) :
Проверим выполняется ли условие остановки итерационного процесса:
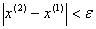
Условие остановки на втором шаге итерации было выполнено лишь для x3, x4, поэтому продолжаем итерацию, вычисляя x(3) :
Проверим выполняется ли условие остановки итерационного процесса:
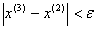
Условие сходимости выполнено на 3-ем шаге .
Корнями уравнения можно принять:
Как видно из вышеизложенных вычислений, скорость сходимости итерационного метода Зейделя выше, чем скорость сходимости метода простой итерации.
Ниже приведена сравнительная таблица1, позволяющая сравнить результаты решения СЛАУ методом простой итерации и методом Зейделя на различных шагах итерации:
Таблица1. Сводная таблица значений элементов приближений двух методов итерации
| № шага | Метод постой итерации | Метод Зейделя | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 |
| i | xi | yi | f(xi,yi) |
| 0 | 0.6 | 1.2 | 0.953971 |
| 1 | 0.8 | 1.3907942 | 1.2071579 |
| 2 | 1 | 1.6322258 | 1.4725082 |
| 3 | 1,2 | 1.9267274 | 1.7488018 |
| 4 | 1,4 | 2.2764878 | 2.0337464 |
| 5 | 1,6 | 2.6832371 | 2.3236155 |
Таблица 2. метод Эйлера (n=20)
| i | xi | yi | f(xi,yi) |
| 0 | 0.6 | 1.2 | 0.953971 |
| 1 | 0.65 | 1.2476986 | 1.0173845 |
| 2 | 0.7 | 1.2985678 | 1.0816058 |
| 3 | 0.75 | 1.3526481 | 1.1466263 |
| 4 | 0.8 | 1.4099794 | 1.2124345 |
| 5 | 0.85 | 1.4706011 | 1.2790158 |
| 6 | 0.9 | 1.5345519 | 1.3463522 |
| 7 | 0,95 | 1.6018695 | 1.414422 |
| 8 | 1 | 1.6725906 | 1.4831991 |
| 9 | 1,05 | 1.7467506 | 1.5526532 |
| 10 | 1,1 | 1.8243832 | 1.6227488 |
| 11 | 1,15 | 1.9055207 | 1.6934454 |
| 12 | 1,2 | 1.9901929 | 1.7646967 |
| 13 | 1,25 | 2.0784278 | 1.8364504 |
| 14 | 1,3 | 2.1702503 | 1.9086477 |
| 15 | 1,35 | 2.2656827 | 1.981223 |
| 16 | 1,4 | 1.4490611 | 1.8231403 |
| 17 | 1,45 | 1.5402182 | 1.8978804 |
| 18 | 1,5 | 1.6351122 | 1.9732751 |
| 19 | 1,55 | 1.7337759 | 2.0492675 |
| 20 | 1,6 | 1.8362393 | 2.1257929 |
4.4 Практическое применение уточненного метода Эйлера для ОДУ
🌟 Видео
Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Алгебраические и аналитические методы решения уравнений и неравенствСкачать

🚀Часть 1. Функциональные уравнения: Погружаемся глубже в математику🔮Скачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

11 класс, 27 урок, Общие методы решения уравненийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

5.1 Численные методы решения уравнений F(x)=0Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Как решать неравенства? Часть 1| МатематикаСкачать

Численные методы. Часть 1Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Решение систем уравнений методом подстановкиСкачать

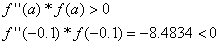
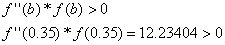
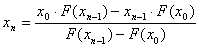
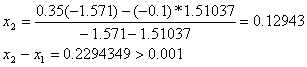
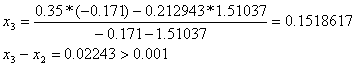
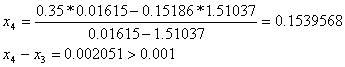
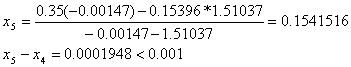
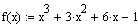
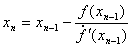
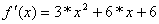
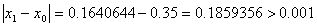
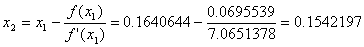
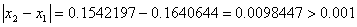
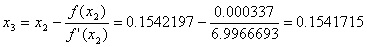
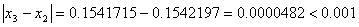
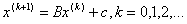
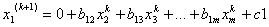
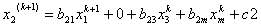
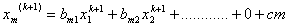
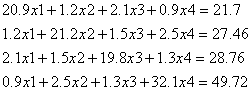

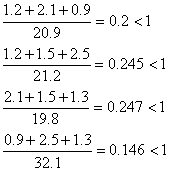
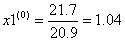
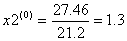
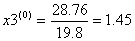
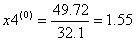
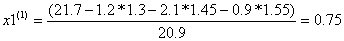
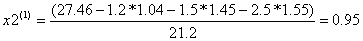
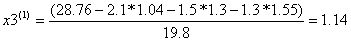
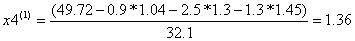
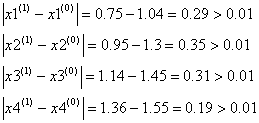
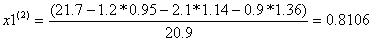
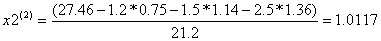
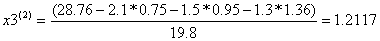
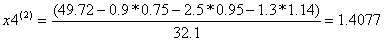
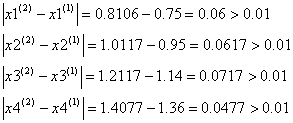
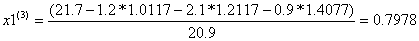
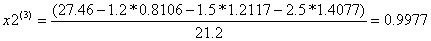
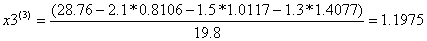
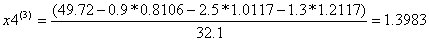
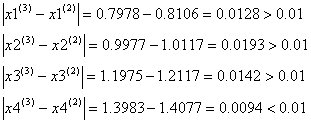
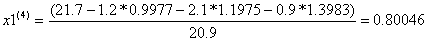
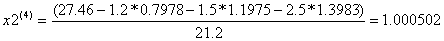
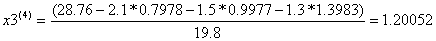
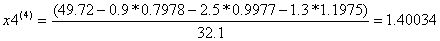
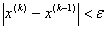
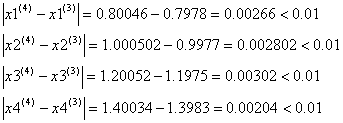
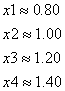
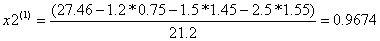
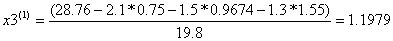
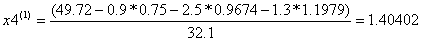
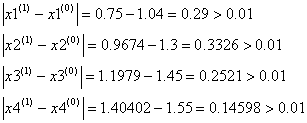

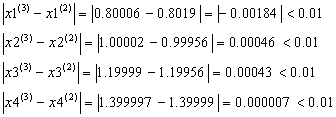
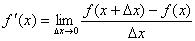
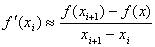 (1)
(1)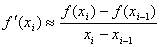 (2)
(2)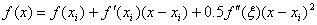
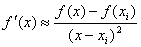 (3)
(3)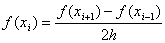 (4)
(4)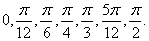
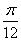
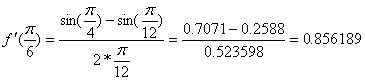
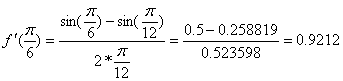
 =cos(
=cos(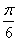 )=0.8660 ,т.е. значение производной, полученное по центрально-симметричной формуле ближе к истинному.
)=0.8660 ,т.е. значение производной, полученное по центрально-симметричной формуле ближе к истинному.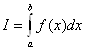
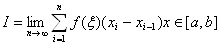
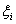 в соответствующем отрезке.
в соответствующем отрезке.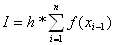 (5)
(5)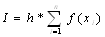 (6)
(6)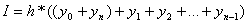
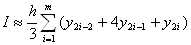
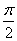 ] на 6 равных отрезков:
] на 6 равных отрезков: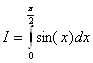 h=
h=
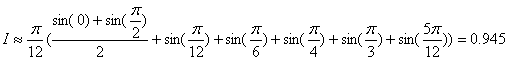
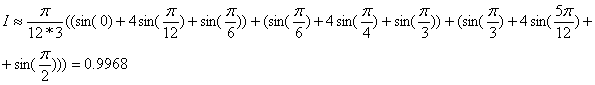
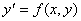 .
.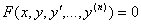 ,
,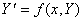 в окрестностях узлов
в окрестностях узлов 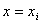 (i=1,2,3,…) и заменим в левой части производную
(i=1,2,3,…) и заменим в левой части производную 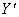 правой разностью. При этом значения функции
правой разностью. При этом значения функции 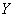 узлах
узлах 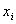 заменим значениями сеточной функции
заменим значениями сеточной функции 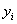 :
: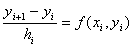
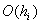 .
.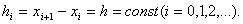
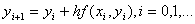
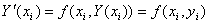 .
.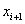 при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным её дифференциалу.
при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным её дифференциалу.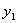 при
при 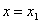 :
: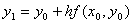 .
.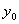 задано начальным условием
задано начальным условием 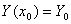 , т.е.
, т.е. 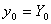 .
.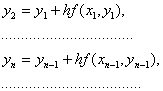
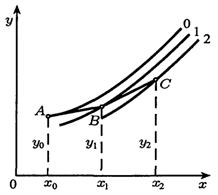
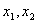 . Интегральные кривые 0,1,2 описывают точные решения уравнения
. Интегральные кривые 0,1,2 описывают точные решения уравнения 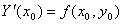 . Погрешность появляется потому, что приращение значения функции при переходе от х0 к х1 заменяется приращением ординаты касательной к кривой 0 в точке А. Касательная ВС уже проводится к другой интегральной кривой 1. таким образом , погрешность метода Эйлера приводит к тому, что на каждом шаге приближенное решение переходит на другую интегральную кривую.
. Погрешность появляется потому, что приращение значения функции при переходе от х0 к х1 заменяется приращением ординаты касательной к кривой 0 в точке А. Касательная ВС уже проводится к другой интегральной кривой 1. таким образом , погрешность метода Эйлера приводит к тому, что на каждом шаге приближенное решение переходит на другую интегральную кривую.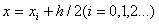 .
.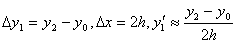 ,
,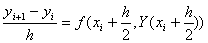 .
.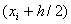 вычислим с помощью метода Эйлера:
вычислим с помощью метода Эйлера: .
.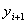 из
из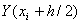 его приближением
его приближением 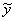 :
: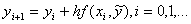
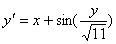 y(0.6)=1.2,
y(0.6)=1.2,