Тема № 3.1. Эквивалентность процентных ставок. Финансовая эквивалентность обязательств
Понятие эквивалентности процентных ставок.
Вывод формул эквивалентности ставок на основе равенства множителей наращения.
Принцип финансовой эквивалентности обязательств.
Достаточно часто в практике возникает ситуация, когда необходимо произвести между собой сравнение по выгодности условий различных финансовых операций и коммерческих сделок. Условия финансово-коммерческих операций могут быть весьма разнообразными и напрямую несопоставимыми. Для сопоставления альтернативных вариантов ставки, используемые в условиях контрактов, приводят к единообразному показателю.
Различные финансовые схемы можно считать эквивалентными в том случае, если они приводят к одному и тому же финансовому результату.
- Понятие эквивалентности процентных ставок. Вывод формул эквивалентности ставок на основе равенства множителей наращения.
Эквивалентные процентные ставки – такие ставки, значения, которых в конкретных условиях приводят к одинаковым финансовым результатам, т.е. замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансовых отношений сторон в рамках одной операции.
Классическим примером эквивалентности являются номинальная и эффективная ставка процентов:
i = (1 + j / m) — 1. номинальная
j = m[(1 + i) — 1]. эффективная
Эффективная ставка измеряет тот относительный доход, который может быть получен в целом за год, т.е. совершенно безразлично – применять ли ставку j при начислении процентов m раз в год или годовую ставку i, – и та, и другая ставки эквивалентны в финансовом отношении.
Поэтому совершенно не имеет значения, какую из приведенных ставок указывать в финансовых условиях, поскольку использование их дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку, а в европейских странах предпочитают эффективную ставку процентов.
Если две номинальные ставки определяют одну и ту же эффективную ставку процентов, то они называются эквивалентными.
Предполагается поместить капитал на 4 года либо под сложную процентную ставку 20% годовых с полугодовым начислением процентов, либо под простую процентную ставку 26% годовых. Найти оптимальный вариант.
Находим для сложной процентной ставки эквивалентную простую ставку:
i = [(1 + j / m) — 1] / n = [(1 + 0,2 / 2) — 1] / 4 = 0,2859.
Таким образом, эквивалентная сложной ставке по первому варианту простая процентная ставка составляет 28,59% годовых, что выше предлагаемой простой ставки в 26% годовых по второму варианту, следовательно, выгоднее разместить капитал по первому варианту, т.е. под 20% годовых с полугодовым начислением процентов.
- Принцип финансовой эквивалентности обязательств.
В практике нередко возникают случаи, когда необходимо заменить одно обязательство другим, например с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи) и т.п. В таких ситуациях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменения контракта.
Эквивалентными считаются такие платежи, которые, будучи «приведены» к одному моменту времени (focal date), оказываются равными.
Приведение осуществляется путем дисконтирования к более ранней дате или, наоборот, наращения суммы платежа (если эта дата относится к будущему).
Если при изменении условий принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить. По существу, принцип эквивалентности следует из формул наращения и дисконтирования, связывающих величины Р и S.
Сумма Р эквивалентна S при принятой процентной ставке и методе ее начисления.
Две суммы денег S1 и S2, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы.
Замена S1 на S2в этих условиях формально не изменяет отношения сторон.
Имеются два обязательства. Условия первого: выплатить 400 тыс. руб. через четыре месяца; условия второго: выплатить 450 тыс. руб. через восемь месяцев. Можно ли считать их равноценными? Так как платежи краткосрочные, то при дисконтировании на начало срока применим простую ставку, равную, допустим, 20%, и получим:


Как видим, сравниваемые обязательства не являются эквивалентными при заданной ставке и в силу этого не могут адекватно заменять друг друга.
В практической деятельности довольно часто возникают ситуации, когда один поток платежей заменяется другим потоком или одним платежом. При этом соблюдается неизменность финансовых отношений сторон до и после заключения контракта или, другими словами, сохраняется финансовая эквивалентность обязательств. Расчет платежей в этом случае базируется на уравнении финансовой эквивалентности.
Уравнением финансовой эквивалентности является равенство сумм заменяемых и заменяющих платежей, приведенных к одному моменту времени.
Принцип финансовой эквивалентности обязательств позволяет, в частности, сравнивать два отдельных платежа, выплачиваемые в различные моменты времени.
Пусть имеются два платежа Sx и S2 со сроками соответственно пх и п2. При оценке этих платежей сравниваются их современные стоимости, и тот платеж считается большим, у которого больше современная стоимость. Иногда возникает необходимость в определении критической ставки /кр, при которой два рассматриваемых платежа оказываются равными. Рассмотрим два варианта.
- Для простых процентов критическая ставка находится из уравнения эквивалентности, получаемого путем приравнивания современных стоимостей первого и второго платежей:
Первый платеж, равный 900 руб., должен быть выплачен через 30 дней, а второй, равный 920 руб., — через 270 дней. Определить критическую ставку при базе сравнения К = 360. Решение. Критическая ставка, при которой платежи эквивалентны, определяется по формуле
- Для сложных процентов уравнение эквивалентности имеет вид:
Первый платеж, равный 9000 руб., должен быть выплачен через 2 года, а второй, равный 12 000 руб., — через 5 лет. Определить критическую ставку.
Критическая ставка, при которой платежи эквивалентны, определяется по формуле (3.18):
Видео:Математика это не ИсламСкачать

амв. 31БД, Финансовая математика, 27 марта 2020. Тема Эквивалентность процентных ставок. Финансовая эквивалентность обязательств Понятие эквивалентности процентных ставок
| Название | Тема Эквивалентность процентных ставок. Финансовая эквивалентность обязательств Понятие эквивалентности процентных ставок |
| Дата | 10.12.2021 |
| Размер | 55.53 Kb. |
| Формат файла |  |
| Имя файла | 31БД, Финансовая математика, 27 марта 2020.docx |
| Тип | Документы #299112 |
| Подборка по базе: Задания для практического занятия . Тема 3.docx, Философия тема 10.docx, Щёголев. 1 темаdocx.docx, Финансирование здравоохранения. Системы ОМС. Модуль 1 тема 2.doc, задачи тема 7.docx, 2 тема Особенности врачебного наблюдения за недоношенными детьми, ИСТОРИЯ ТЕМА 5.docx, Лекция. Тема 1. Система координат.pdf, Задания Тема 9.docx, Примерная тематика курсовых работ.docx Тема № 3.1. Эквивалентность процентных ставок. Финансовая эквивалентность обязательств Понятие эквивалентности процентных ставок. Вывод формул эквивалентности ставок на основе равенства множителей наращения. Принцип финансовой эквивалентности обязательств. Достаточно часто в практике возникает ситуация, когда необходимо произвести между собой сравнение по выгодности условий различных финансовых операций и коммерческих сделок. Условия финансово-коммерческих операций могут быть весьма разнообразными и напрямую несопоставимыми. Для сопоставления альтернативных вариантов ставки, используемые в условиях контрактов, приводят к единообразному показателю. Различные финансовые схемы можно считать эквивалентными в том случае, если они приводят к одному и тому же финансовому результату.
Эквивалентные процентные ставки – такие ставки, значения, которых в конкретных условиях приводят к одинаковым финансовым результатам, т.е. замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансовых отношений сторон в рамках одной операции. Классическим примером эквивалентности являются номинальная и эффективная ставка процентов: i = (1 + j / m) — 1. номинальная j = m[(1 + i) — 1]. эффективная Эффективная ставка измеряет тот относительный доход, который может быть получен в целом за год, т.е. совершенно безразлично – применять ли ставку j при начислении процентов m раз в год или годовую ставку i, – и та, и другая ставки эквивалентны в финансовом отношении. Поэтому совершенно не имеет значения, какую из приведенных ставок указывать в финансовых условиях, поскольку использование их дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку, а в европейских странах предпочитают эффективную ставку процентов. Если две номинальные ставки определяют одну и ту же эффективную ставку процентов, то они называются эквивалентными. Предполагается поместить капитал на 4 года либо под сложную процентную ставку 20% годовых с полугодовым начислением процентов, либо под простую процентную ставку 26% годовых. Найти оптимальный вариант. Находим для сложной процентной ставки эквивалентную простую ставку: i = [(1 + j / m) — 1] / n = [(1 + 0,2 / 2) — 1] / 4 = 0,2859. Таким образом, эквивалентная сложной ставке по первому варианту простая процентная ставка составляет 28,59% годовых, что выше предлагаемой простой ставки в 26% годовых по второму варианту, следовательно, выгоднее разместить капитал по первому варианту, т.е. под 20% годовых с полугодовым начислением процентов.
В практике нередко возникают случаи, когда необходимо заменить одно обязательство другим, например с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи) и т.п. В таких ситуациях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменения контракта. Замена S1 на S2в этих условиях формально не изменяет отношения сторон. Имеются два обязательства. Условия первого: выплатить 400 тыс. руб. через четыре месяца; условия второго: выплатить 450 тыс. руб. через восемь месяцев. Можно ли считать их равноценными? Так как платежи краткосрочные, то при дисконтировании на начало срока применим простую ставку, равную, допустим, 20%, и получим: Как видим, сравниваемые обязательства не являются эквивалентными при заданной ставке и в силу этого не могут адекватно заменять друг друга.
В практической деятельности довольно часто возникают ситуации, когда один поток платежей заменяется другим потоком или одним платежом. При этом соблюдается неизменность финансовых отношений сторон до и после заключения контракта или, другими словами, сохраняется финансовая эквивалентность обязательств. Расчет платежей в этом случае базируется на уравнении финансовой эквивалентности. Уравнением финансовой эквивалентности является равенство сумм заменяемых и заменяющих платежей, приведенных к одному моменту времени. Принцип финансовой эквивалентности обязательств позволяет, в частности, сравнивать два отдельных платежа, выплачиваемые в различные моменты времени. Пусть имеются два платежа Sx и S2 со сроками соответственно пх и п2. При оценке этих платежей сравниваются их современные стоимости, и тот платеж считается большим, у которого больше современная стоимость. Иногда возникает необходимость в определении критической ставки /кр, при которой два рассматриваемых платежа оказываются равными. Рассмотрим два варианта.
Первый платеж, равный 900 руб., должен быть выплачен через 30 дней, а второй, равный 920 руб., — через 270 дней. Определить критическую ставку при базе сравнения К = 360. Решение. Критическая ставка, при которой платежи эквивалентны, определяется по формуле
Пример. Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать  Финансовая эквивалентность платежей.3.1 Эквивалентность процентных ставок. Эквивалентные ставки —это ставки разного вида, которые в однотипных операциях приводят к одинаковым результатам. Например, простая ставка 22% годовых будет эквивалентна сложной ставке 20% годовых для кредита 10 000 рублей сроком 2 года, т.к. в каждом случае сумма погашения кредита будет одинакова: Замена в договоре одной ставки на эквивалентную ей ставку другого вида не меняет результатов операции. В качестве результата операции удобно брать наращенную сумму, множитель наращения или проценты. Формулы для эквивалентных ставок получают из уравнения эквивалентности, в котором приравниваются результаты операций: 1) эквивалентность простых и сложных ставок: 2) эквивалентность сложной и номинальной ставок: 3) эквивалентность по простой и учетной ставке: Эквивалентные ставки простых и сложных процентов называют – доходностью операции. 3.2 Доходность нескольких однотипных операций. Доходность нескольких однотипных операций находят с помощью средней ставки. Средняя ставка— это эквивалентная ставка простых процентов, которая приводит к тому же результату, что и фактические ставки операций. В качестве результата рассматривают сумму простых процентов: , где iпр — средняя ставка Получили формулу средней арифметической взвешенной 3.3 Финансовая эквивалентность платежей. Эквивалентные платежи –это платежи, которые будут равны, если их привести к одному и тому же сроку по одной и той же процентной ставке. Чтобы привести платеж к более позднему сроку, необходимо начислить проценты на платеж: S — приведенный платеж, n — срок до приведения. Чтобы привести платеж к более раннему сроку необходимо дисконтировать платеж (т.е. удержать проценты): Приведение платежей используется в ситуациях, когда необходимо: — изменить сроки платежей; — поменять количество платежей; — объединить несколько платежей в один – консолидация платежей. В этих случаях, чтобы ни одна из сторон не понесла убытки, руководствуются принципом финансовой эквивалентности платежей, когда все платежи приводятся к одному сроку и приравниваются результаты по старым и новым условиям: где S – размер приведенного платежа по старым условиям, S*- размер приведенного платежа по новым условиям, К — количество старых платежей, N — количество новых платежей. В случае объединения платежей, все платежи приводят к сроку нового консолидированного платежа, и поэтому, принципы финансовой эквивалентности преобразовывается к виду: Дата добавления: 2015-11-26 ; просмотров: 4616 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ 🔍 ВидеоФинансовая математика. Лекция 3. Эквивалентность процентных ставок финансовых обязательствСкачать  Логическая функция - Эквивалентность. Таблица истинности и свойстваСкачать  95 Разбиение множества на классы эквивалентностиСкачать  Отношение эквивалентности, отношение порядкаСкачать  Олегу Тинькову запрещён вход на Мехмат МГУСкачать  3.3 Отношение эквивалентности | Роман Попков | ИТМОСкачать  Вычисление пределов с помощью эквивалентных функций.Скачать  КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать  Финансовая математика. Лекция 5. Постоянные финансовые рентыСкачать  Эквивалентные системы линейных уравнений | Системы уравнений | Алгебра I (9 видео)Скачать  Формула замены эквивалентности || Как избавиться от эквивалентностиСкачать  Эквивалентные бесконечно малыеСкачать  NPV, PI, DPP, IRR. Чистая приведенная стоимость и дисконтирование #npv #irr #excel #дисконтированиеСкачать  Финансовая математика. Лекция 1. Простые проценты.Скачать  Дисконтирование - самое понятное объяснениеСкачать  Отношения эквивалентностиСкачать  Финансовая математика. Лекция 2. Сложные проценты.Скачать  Интуитивная топология | теоретикомнож. вопр. | бинарные отношения | отношение эквивалентности | 1Скачать  |




 = 375,00
= 375,00 = = 397,06 тыс. руб.
= = 397,06 тыс. руб.


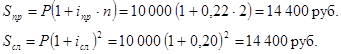
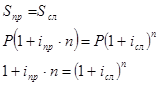
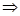
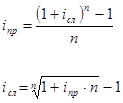
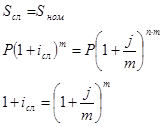
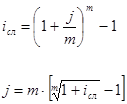
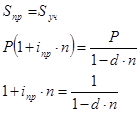
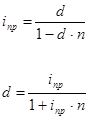
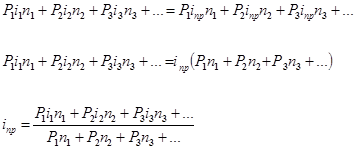
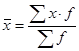 , поэтому эквивалентную простую ставку называют средней ставкой:
, поэтому эквивалентную простую ставку называют средней ставкой: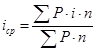
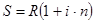 , где R — исходный платеж,
, где R — исходный платеж,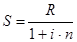
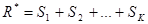 , где
, где 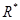 -консолидированный платеж.
-консолидированный платеж.