Спираль архимеда как построить уравнение (3 видео)

Спираль Архимеда

Первый ученый который открыл и изучил свойства этой линии, был великий математик и философ из древней Греции, Архимед. Его именем она и была названа.

Содержание

Построение спирали Архимеда
Шаг спирали Архимеда
Полярное уравнение спирали Архимеда
Уравнения кривых. Спираль Архимеда.
Упражнения
🎬 Видео

Видео:§6 Спираль АрхимедаСкачать

Построение спирали Архимеда

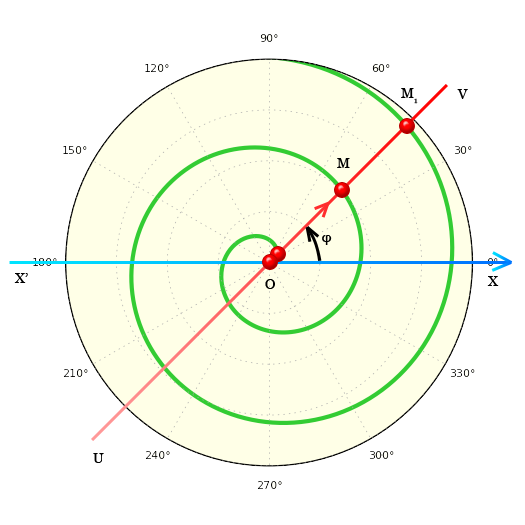
Некоторая прямая UV изначально совпадает с прямой XX`. Прямая UV равномерно вращается относительно точки O. По прямой UV равномерно перемещается точка M отдаляясь от точки O. В результате точка M, перемещаясь по вышеуказанным правилам, описывает линию — спираль Архимеда.

Видео:Спираль Архимеда построениеСкачать

Шаг спирали Архимеда

При повороте прямой UV из любого положения на некоторый угол Δφ точка M смещается на расстояние Δρ. Смещение MM₁ происходит за один оборот прямой UV, и всегда равно одному и тому же числу. Это число называется шагом спирали Архимеда

Видео:Длина параболы и спирали Архимеда: что у них общего?Скачать

Полярное уравнение спирали Архимеда

В этом уравнении можно перейти от шага спирали Архимеда a к параметру спирали Архимеда k

Тогда уравнение спирали примет вид

При повороте прямой UV на один радиан, точка M смещается на расстояние равное Параметру спирали Архимеда.

Видео:Архимедова Спираль КОМПАС 3DСкачать

Уравнения кривых. Спираль Архимеда.

Архимедова спираль — плоская кривая сформированная траекторией произвольной точки, которая размеренно двигается по лучу берущему свое начало в O, одновременно с этим сам луч размерено обращается вокруг O. Перефразировав получаем, расстояние ρ пропорционально углу оборота φ луча. Обороту луча на одинаковый угол соответствует одно и то же увеличение ρ.

Уравнение, характеризующее Архимедову спираль, в полярной системе координат:

где k — сдвиг точки M по лучу r, при обороте на угол, который равен одному радиану.

Обороту прямой на 2π соответствует смещение a = 2kπ.

Число a — шаг спирали.

На основании этого уравнение Архимедовой спирали можно представить таким образом:

Когда поворачиваем луч против движения часовой стрелки, получаем правую спираль, когда поворачиваем — по часовой стрелке — левую спираль. При положительной величине φ формируется правая спираль, отрицательной — левая спираль.

Видео:Построение эвольвенты окружностиСкачать

Упражнения

1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .

2. Нарисуйте кривую, задаваемую уравнением r = cos φ .

3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

4. Докажите, что уравнение

задает эллипс, если 0 > 1.

5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?

6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?

7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = .

8. Нарисуйте спираль Галилея , которая задается уравнением r = a 2 ( a > 0). Она вошла в историю математики в XVII веке в связи с задачей нахождения формы кривой, по которой двигается свободно падающая в области экватора точка, не обладающая начальной скоростью, сообщаемой ей вращением земного шара.

9. Нарисуйте кривую, задаваемую уравнением r = | |.

10. Нарисуйте кривую, задаваемую уравнением r = .

11. Нарисуйте кривую, задаваемую уравнением r = .

12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.

1. Березин В. Кардиоида //Квант. – 1977. № 12.

2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.

3. Берман Г.Н. Циклоида. – М.: Наука, 1975.

4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.

5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.

6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.

7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.

8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.

9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.

10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.