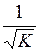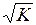Построение уравнения регрессии начинается с решения вопроса о спецификации модели, т.е. формулировки вида модели, исходя из теории, устанавливающей связь между явлениями. Она включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным.
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции, а также влияние лишней переменной и недоучет в уравнении регрессии какого-либо существенного фактора.
Влияние неучтенной переменной.
Пусть 
Будем рассматривать ложную модель 

Т.о. по МНК: 
А на самом деле: 
Т.е. 

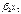
Рассмотрим величину смещения оценки 
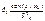
В истинной модели 










Это замещение возможно, т.к. 




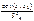
Влияние лишней переменной.
Пусть 
Будем рассматривать ложную модель 

Т.к. на самом деле 


При этом 
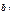
Однако 
Т.о. оценка 

Мультиколлинеарность.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Включаемые во множественную регрессию факторы должны объяснять вариацию независимой переменной. При дополнительном включении в регрессию фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, то включаемый фактор не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по критерию Стьюдента.
3. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, когда 

Отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции.
Матрица коэффициентов корреляции:
| y | x | z | v |
| y | |||
| x | 0,8 | ||
| z | 0,7 | 0,8 | |
| v | 0,6 | 0,5 | 0,2 |
Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 

Если факторы явно коллинеарны, то они дублируют друг друга, и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
Очевидно, что факторы x и z дублируют друг друга. В анализ целесообразно включить фактор z, а не х, так как корреляция z с результатом у слабее, чем корреляция фактора х с у ( 

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов.
Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга.
Мультиколлинеарность – ситуация, при которой линейная зависимость между независимыми переменными приводит к получению неэффективных, ненадежных оценок линейной регрессии.
Реальная (частичная) мультиколлинеарность возникает в случае существования достаточно тесных статистических связей между объясняющими переменными.
Наличие мультиколлинеарности факторов может означать, что некоторые факторы всегда будут действовать вместе. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК:
предполагается, что 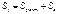
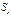





В свою очередь, при независимости факторов друг от друга выполнимо равенство
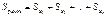

Если же факторы интеркоррелированы, то данное равенство нарушается.
Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
· Затрудняется интерпретация параметров множественной регрессии; параметры линейной регрессии теряют экономический смысл;
· Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делают модель непригодной для анализа и прогнозирования.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции была бы единичной матрицей, поскольку все недиагональные элементы были бы равны 0. Так для уравнения регрессии, включающего три объясняющих переменных, матрица парных коэффициентов корреляции имела бы определитель, равный 1:

Если же между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:

Чем ближе к нулю определитель матрицы, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы, чем меньше мультиколлинеарность факторов.
Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных Н0: 
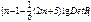



Существует ряд подходов преодоления сильной межфакторной корреляции.
1) Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов.
2) Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Например, при построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней 
3) Используются такие методы, которые сводят к нулю межфакторную корреляцию, т.е. переходят от исходных переменных к их линейным комбинациям, не коррелированных друг с другом (метод главных компонент: с помощью метода главных компонент осуществляется переход к ортогонализированным объясняющим переменным. Эти новые объясняющие переменные представляют собой некоторые линейные комбинации исходных регрессоров, выбранные так, чтобы корреляции между ними были малы или вообще отсутствовали).
4) Решению проблемы устранения мультиколлинеарности факторов может помочь переход к уравнениям приведенной формы. С этой целью в уравнение регрессии производится подстановка рассматриваемого фактора через выражение его из другого уравнения.
5) К способам снижения мультиколлинеарности можно отнести увеличение объема выборки; увеличение 



Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Оценка параметров линейных уравнений регрессии
Спецификация модели
+наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов
-раздел экономической теории, связанный с анализом статистической информации
-специальный раздел математики, посвященный анализу экономической информации
-наука, которая осуществляет качественный анализ взаимосвязей экономических явлений и процессов
#Основной задачей эконометрики является…
+исследование взаимосвязей экономических явлений и процессов
-отражение особенностей социального развития общества
-установление связей между различными процессами в обществе и технических процессом
— анализ технического прогресса на примере социально–экономических показателей
#При выборе спецификации модели парная регрессия используется в случае, когда …
+среди множества факторов, влияющих на результат можно выделить доминирующий фактор
-среди множества факторов, влияющих на результат нельзя выделить доминирующий фактор
-среди множества факторов, влияющих на результат можно выделить несколько факторов
-среди множества факторов, влияющих на результат можно выделить лишь случайные факторы
#Объем выборки должен превышать число рассчитываемых параметров при исследуемых факторах …
#К ошибкам спецификации относится …
+неправильный выбор той или иной математической функции
-однородность выбранной совокупности
-учет в модели случайных факторов
— учет в модели существенных факторов
#Относительно формы зависимости различают …
+линейную и нелинейную регрессии
-простую и множественную регрессии
-непосредственную и косвенную регрессии
-положительную и отрицательную регрессии
#Относительно количества факторов, включенных в уравнение регрессии различают …
+простую и множественную регрессии
-линейную и нелинейную регрессии
-непосредственную и косвенную регрессии
— множественную и многофакторную регрессии
#Простая линейная регрессия предполагает …
+наличие одного фактора и линейность уравнения регрессии
-наличие двух и более факторов и линейность уравнения регрессии
-наличие одного фактора и нелинейность уравнения регрессии
-наличие двух и более факторов и нелинейность уравнения регрессии
#Объем выборки определяется …
+числом параметров при независимых переменных
-числом результативных переменных
-объемом генеральной совокупности
-числовыми значениями переменных отбираемых в выборку
#Дано уравнение регрессии 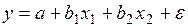
+линейное уравнение множественной регрессии
-линейное уравнение простой регрессии
-полиномиальное уравнение множественной регрессии
— полиномиальное уравнение парной регрессии
#Выбор формы зависимости экономических показателей и определение количества факторов в модели называется _____________ эконометрической модели.
#Коэффициент парной корреляции характеризует …
+тесноту линейной связи между двумя переменными
-тесноту нелинейной связи между двумя переменными
-тесноту линейной связи между несколькими переменными
-тесноту нелинейной связи между несколькими переменными
#Мультиколлинеарность факторов эконометрической модели подразумевает …
+наличие линейной зависимости между более чем двумя факторами
-наличие линейной зависимости между двумя факторами
-отсутствие зависимости между факторами
-наличие нелинейной зависимости между двумя факторами
#Взаимодействие факторов эконометрической модели означает, что …
+факторы дублируют влияние друг друга на результат
-влияние одного из факторов на результирующий признак не зависит от значений другого фактора
-влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов
— влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора
#Отбор факторов в модель множественной регрессии при помощи метода включения основан на сравнении значений …
+остаточной дисперсии до и после включения фактора в модель
-общей дисперсии до и после включения фактора в модель
-дисперсии до и после включения результата в модель
-остаточной дисперсии до и после включения случайных факторов в модель
#Величина остаточной дисперсии при включении существенного фактора в модель …
— будет равна нулю
#В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между …
-параметрами и переменными
-переменными и случайными факторами
#Матрица парных коэффициентов корреляции строится для выявления коллинеарных и мультиколлинеарных …
#Факторы эконометрической модели являются коллинеарными, если коэффициент …
+корреляции между ними по модулю больше 0,7
-детерминации между ними по модулю больше 0,7
-корреляции между ними по модулю меньше 0,7
-детерминации между ними по модулю меньше 0,7
#Из пары коллинеарных факторов в эконометрическую модель включается тот фактор …
+который при достаточно тесной связи с результатом имеет меньшую связь с другими факторами
-который при который при отсутствии связи с результатом имеет меньшую связь с другими факторами
-который при отсутствии связи с результатом имеет максимальную связь с другими факторами
-который при достаточно тесной связи с результатом имеет наибольшую связь с другими факторами
#Величина коэффициента детерминации при включении существенного фактора в эконометрическую модель …
-существенно не изменится
— будет равна нулю
#Основным требованием к факторам, включаемым в модель множественной регрессии, является …
+отсутствие взаимосвязи между факторами
-наличие тесной взаимосвязи между факторами
-отсутствие взаимосвязи между результатом и фактором
-отсутствие линейной взаимосвязи между факторами
#Фиктивными переменными в уравнении множественной регрессии являются …
+качественные переменные, преобразованные в количественные
-дополнительные количественные переменные, улучшающие решение
-комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели
-переменные, представляющие простейшие функции от уже включенных в модель переменных
#В качестве фиктивных переменных в модель множественной регрессии включаются факторы, …
+не имеющие количественных значений
-имеющие количественные значения
-не имеющие качественных значений
— имеющие вероятностные значения
#При включении фиктивных переменных в модель им присваиваются …
#Исходные значения фиктивных переменных предполагают значения …
#Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться ____________ работника
#Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является __________ потребителя
#Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются …
#Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков …
#Фиктивные переменные включаются в уравнения __________ регрессии
#Одним из методов присвоения числовых значений фиктивным переменным является …
-нахождение среднего значения
-выравнивание числовых значений по убыванию
-выравнивание числовых значений по возрастанию
#Методом присвоения числовых значений фиктивным переменным не является …
+нахождение среднего значения
-присвоение цифровых меток
-присвоение количественных значений
#Величина коэффициента регрессии показывает …
+среднее изменение результата при изменении фактора на одну единицу
-характер связи между фактором и результатом
-тесноту связи между фактором и результатом
-тесноту связи между исследуемыми факторами
#Величина параметра a в уравнении парной линейной регрессии 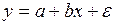
+результирующей переменной при нулевом значении фактора
-факторной переменной при нулевом значении результата
-результирующей переменной при нулевом значении случайной величины
-факторной переменной при нулевом значении случайного фактора
#Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированном на среднем уровне значении других переменных называется …
#В линейном уравнении парной регрессии 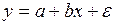
#Линейное уравнение множественной регрессии имеет вид 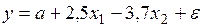
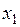
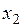
+по этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой
— 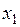
— 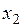
-оказывают одинаковое влияние
#В стандартизованном уравнении множественной регрессии 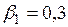
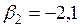
+ 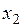
— 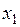
-по этому уравнению нельзя ответить на поставленный вопрос, так как стандартизованные коэффициенты регрессии несравнимы между собой
-по этому уравнению нельзя ответить на поставленный вопрос, так как неизвестны значения «чистых» коэффициентов регрессии
#Построена модель парной регрессии зависимости предложения от цены 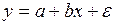
+случайной величины ε
-посредством константы ε
-случайной величины x
-посредством параметра b
#Для модели зависимости дохода населения (р.) от объема производства (млн. р.) получено уравнение у = 0,003х + 1200 + ε. При изменении объема производства на 1 млн. р. доход в среднем изменится на …
#В стандартизованном уравнении множественной регрессии переменными являются …
-средние значения исходных переменных
#Показатель, характеризующий на сколько сигм изменится в среднем результат при изменении соответствующего фактора на одну сигму, при неизменном уровне других факторов называется __________ коэффициентом регрессии
#В стандартизованном уравнении свободный член …
-равен коэффициенту множественной корреляции
-равен коэффициенту множественной детерминации
Оценка параметров линейных уравнений регрессии
#Метод наименьших квадратов используется для оценивания …
+параметров линейной регрессии
-величины коэффициента корреляции
-величины коэффициента детерминации
-средней ошибки аппроксимации
#Метод наименьших квадратов не применимдля …
+уравнений нелинейных по оцениваемым параметрам
-линейных уравнений множественной регрессии
-линейных уравнений парной регрессии
-полиномиальных уравнений множественной регрессии
#В основе метода наименьших квадратов лежит …
+минимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-равенство нулю суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-максимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-минимизация суммы квадратов отклонений фактических значений результативного признака от его средних значений
#Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить …
-методом первых разностей
-методом скользящего среднего
#В исходном соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений …
-приравнивается к нулю
-приравнивается к системе нормальных уравнений
#Метод наименьших квадратов позволяет оценить _____________ уравнений регрессии
-параметры и переменные
-переменные и случайные величины
#Оценки параметров уравнений регрессии при помощи метода наименьших квадратов находятся на основании решения …
+решения системы нормальных уравнений
-решения двойственной задачи
-решения уравнения регрессии
-решения системы нормальных неравенств
#Оценки параметров линейного уравнения множественной регрессии можно найти при помощи метода …
+метода наименьших квадратов
-метода наибольших квадратов
-метода средних квадратов
-метода нормальных квадратов
#Метод наименьших квадратов применяется для оценки …
+параметров линейных уравнений регрессии
-качества линейных уравнений регрессии
-уравнений регрессии, нелинейных по параметрам
-качества уравнений, нелинейных по параметрам
#Система нормальных уравнений метода наименьших квадратов строится на основании …
+таблицы исходных данных
-предсказанных значений результативного признака
-отклонений фактических значений результативного признака от его теоретических значений
-отклонений фактических значений объясняющей переменной от ее теоретических значений
#Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является …
-равенство нулю средних значений результативной переменной
-равенство нулю средних значений факторного признака
#Несмещенность оценки характеризует …
+равенство нулю математического ожидания остатков
-наименьшую дисперсию остатков
-увеличение точности ее вычисления с увеличением объема выборки
-ее зависимость от объема выборки
#Если оценка параметра эффективна, то это означает …
+наименьшую дисперсию остатков
-равенство нулю математического ожидания остатков
-максимальную дисперсию остатков
-уменьшение точности с увеличением объема выборки
#Состоятельность оценки характеризуется .
+увеличением ее точности с увеличением объема выборки
-независимостью от объема выборки значения математического ожидания остатков
-уменьшением ее точности с увеличением объема выборки
-зависимостью от объема выборки значения математического ожидания остатков
#Несмещенность оценки на практике означает …
+что при большом числе выборочных оцениваний остатки не будут накапливаться
-что найденное значение коэффициента регрессии нельзя рассматривать как среднее значение из возможного большого количества несмещенных оценок
-невозможность перехода от точечного оценивания к интервальному
-уменьшение точности с увеличением объема выборки
#Эффективность оценки на практике характеризуется …
+возможностью перехода от точечного оценивания к интервальному
-отсутствием накапливания значений остатков при большом числе выборочных оцениваний
-невозможностью перехода от точечного оценивания к интервальному
-уменьшением точности с увеличением объема выборки
#Свойствами оценок МНК являются …
+эффективность, состоятельность и несмещенность
-эффективность, состоятельность и смещенность
-эффективность, несостоятельность и смещенность
-эффективность, несостоятельность и несмещенность
#Увеличение точности оценок с увеличением объема выборки описывает свойство _______ оценки.
#Математическое ожидание остатков равно нулю, если оценки параметров обладают свойством …
#Минимальная дисперсия остатков характерна для оценок, обладающих свойством …
#Переход от точечного оценивания к интервальному возможен, если оценки являются …
+ эффективными и несмещенными
-эффективными и несостоятельными
-неэффективными и состоятельными
-состоятельными и смещенными
#При примени метода наименьших квадратов исследуются свойства …
+оценок параметров уравнения регрессии
-оценок переменных уравнения регрессии
-оценок случайных величин уравнения регрессии
-оценок переменных и параметров уравнения регрессии
+одинаковую дисперсию остатков при каждом значении фактора
-рост дисперсии остатков с увеличением значения фактора
-уменьшение дисперсии остаток с уменьшением значения фактора
-максимальную дисперсию остатков при средних значениях фактора
#Предпосылкой метода наименьших квадратов является то, что…
+остаточные величины имеют случайный характер
-остаточные величины имеют неслучайный характер
-при увеличении моделируемых значений результативного признака значение остатка увеличивается
-при уменьшении моделируемых значений результативного признака значение остатка уменьшается
+зависимость дисперсии остатков от значения фактора
-постоянство дисперсии остатков независимо от значения фактора
-независимость математического ожидания остатков от значения фактора
-зависимость математического ожидания остатков от значения фактора
#Предпосылкой метода наименьших квадратов является то, что остатки…
+подчиняются закону нормального распределения
-не подчиняются закону нормального распределения
-подчиняются закону больших чисел
-не подчиняются закону больших чисел
#Предпосылки метода наименьших квадратов исследуют поведение …
-параметров уравнения регрессии
-переменных уравнения регрессии
#Предпосылкой метода наименьших квадратов является …
+отсутствие автокорреляции в остатках
-присутствие автокорреляции в остатках
-отсутствие корреляции между результатом и фактором
-присутствие автокорреляции между результатом и фактором
#Предпосылкой метода наименьших квадратов не является условие …
+неслучайного характера остатков
-отсутствия автокорреляции в остатках
-случайного характера остатков
#Случайный характер остатков предполагает …
+независимость остатков от величины предсказанных по модели значений результативного признака
-зависимость остатков от величины предсказанных по модели значений результативного признака
-зависимость предсказанных по модели значений результативного признака от значений факторного признака
-независимость предсказанных по модели значений результативного признака от значений факторного признака
#Отсутствие автокорреляции в остатках предполагает, что значения ______ не зависят друг от друга
#Оценки параметров, найденные при помощи метода наименьших квадратов обладают свойствами эффективности, состоятельности и несмещенности, если предпосылки метода наименьших квадратов …
-можно не учитывать
#Если предпосылки метода наименьших квадратов нарушены, то …
+оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности
-коэффициент регрессии является несущественным
-коэффициент корреляции является несущественным
-полученное уравнение статистически незначимо
#Обобщенный метод наименьших квадратов применяется в случае…
#Обобщенный метод наименьших квадратов используется для корректировки…
+гетероскедастичности остатков в уравнении регрессии
-автокорреляции между независимыми переменными
-параметров нелинейного уравнения регрессии
-точности определения коэффициента множественной корреляции
#Обобщенный метод наименьших квадратов подразумевает …
-линеаризацию уравнения регрессии
-двухэтапное применение метода наименьших квадратов
-переход от множественной регрессии к парной
#Обобщенный метод наименьших квадратов рекомендуется применять в случае …
-нормально распределенных остатков
-автокорреляции результативного признака
#При применении метода наименьших остатков уменьшить гетероскедастичность остатков удается путем …
-введения дополнительных факторов в модель
-введения дополнительных результатов в модель
#На основании преобразования переменных при помощи обобщенного метода наименьших квадратов получаем новое уравнение регрессии, которое представляет собой …
+взвешенную регрессию, в которой переменные взяты с весами
-нелинейную регрессию, в которой переменные взяты с весами
-взвешенную регрессию, в которой переменные взяты с весами
-нелинейную регрессию, в которой переменные взяты с весами
#Обобщенный метод наименьших квадратов не используется для моделей с _______ остатками
-автокоррелярованными и гетероскедастичными
#Что преобразуется при применении обобщенного метода наименьших квадратов?
+исходные уровни переменных
-дисперсия результативного признака
-дисперсия факторного признака
-стандартизованные коэффициенты регрессии
#Обобщенный метод наименьших квадратов отличается от обычного МНК тем, что при применении ОМНК…
+преобразуются исходные уровни переменных
-уменьшается количество наблюдений
-остатки приравниваются к нулю
-остатки не изменяются
#После применения обобщенного метода наименьших квадратов удается избежать ______ остатков
-равенства нулю суммы
#Метод оценки параметров моделей с гетероскедастичными остатками называется …методом наименьших квадратов
Видео:Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

Спецификация модели множественной регрессии
Основной целью множественной регрессии является построение модели с большим числом факторов и определение при этом влияния каждого из факторов в отдельности на результат, а так же определение совокупного воздействия факторов на моделированный показатель.
Спецификация модели множественной регрессии включает в себя отбор фактора и выбор вида математической функции (выбор вида уравнения регрессии). Факторы, включаемые во множественную регрессию должны быть количественно измеримы и не должны быть интеркоррелированы и тем более находиться в точной функциональной связи (т.е. должны в меньшей степени влиять друг на друга, а в большей степени на результативный признак).
Включаемые во множественную регрессию факторы должны объяснять вариацию независимой переменной. Например, если строится модель с набором 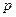

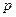
Влияние других неучтенных факторов в модели оценивается как 
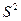
При включении в модель дополнительного 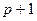

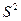

Отбор факторов для множественной регрессии осуществляется в две стадии:
1. Подбираются факторы, исходя из сущности проблемы.
2. На основе матрицы показателей корреляции определяют 
Коэффициенты корреляции между объясняющими переменными 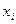
Две переменные 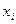

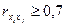
Если переменные явно коллинеарны, то они находятся в сильной линейной зависимости.
При наличии явно коллинеарных переменных предпочтение отдается не фактору более тесно связанному с результатом, а фактору, который при этом имеет наименьшую тесноту связи с другими факторами.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллениарность факторов.
При использовании множественной регрессии может возникнуть мультиколлениарность фактов, т.е. более чем два фактора связаны между собой линейной зависимостью. В таких случаях менее надежным становится МНК при оценке отдельных факторов, результатом чего становится затруднение интерпретации параметров множественной регрессии как характеристик действия фактора в чистом виде. Параметры линейной регрессии теряют экономический смысл, оценки параметров ненадежны, возникают большие стандартные ошибки, которые при этом могут изменяться с изменением объема наблюдений, т.е. модель становится непригодной для анализа и прогнозирования экономической ситуации. Для оценки мультиколлениарности фактора используют следующие методы:
1. Определение матрицы парных коэффициентов корреляции между факторами, например, если задана линейная модель множественной регрессии 
Если значение данного определителя равно 1

то факторы являются неколлинеарными между собой.
Если между факторами существует полная линейная зависимость, то все коэффициенты парной корреляции равны 1, в результате чего

2. Метод испытания гипотезы о независимости переменных. В этом случае нулевая гипотеза 
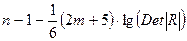


Если 
Определяя и сравнивая между собой коэффициенты множественной детерминации фактора, используя в качестве зависимой переменной последовательно каждой из факторов можно определить факторы, ответственные за мультиколлениарность, т.е. фактор с наибольшим значением величины 
Существуют следующие способы преодоления сильной межфакторной корреляции:
1) исключение из модели одного или несколько данных;
2) преобразование факторов для уменьшения корреляции;
3) совмещение уравнения регрессии, которые будут отражать не только факторы, но и их взаимодействие;
4) переход уравнения приведенной формы и др.
При построении уравнения множественной регрессии одним из важнейших этапов является отбор факторов, включаемых в модель. Различные подходы к отбору факторов на основе показателей корреляции к различным методам, среди которых наиболее применимы:
1) Метод исключения – производится отсев данных;
2) Метод включения – вводят дополнительный фактор;
3) Шаговый регрессионный анализ – исключают ранее введенный фактор.
При отборе факторов применяют следующее правило: число включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой строится модель.
Используются линейное и нелинейное уравнение множественной регрессии. Среди нелинейных моделей множественной регрессии наиболее часто применяется степенная модель. В общем виде нелинейное уравнение множественной регрессии: 




Коэффициент «чистой регрессии» 

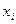
Параметр 




💡 Видео
Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Эконометрика. Линейная парная регрессияСкачать

Эконометрика 08 Множественная регрессияСкачать

Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Множественная регрессияСкачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать

Математика #1 | Корреляция и регрессияСкачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Точечный прогноз. Интервальный прогноз. Построение уравнения регрессии с помощью анализа данныхСкачать

РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать

Парная регрессия: линейная зависимостьСкачать

Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Выбор факторов, влияющих на результативный показательСкачать

Эконометрика. Неделя 1. Суть метода наименьших квадратов.Скачать

Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать