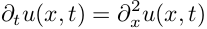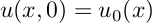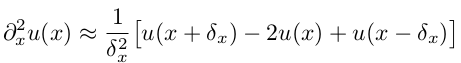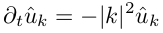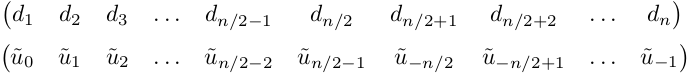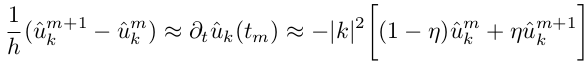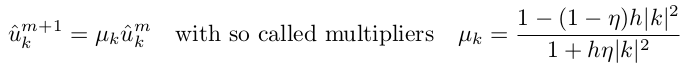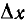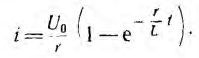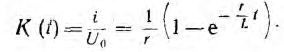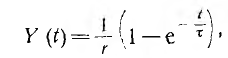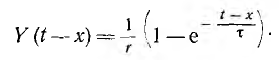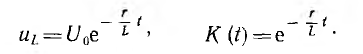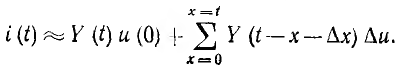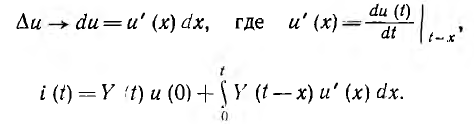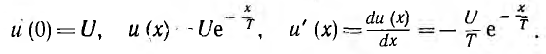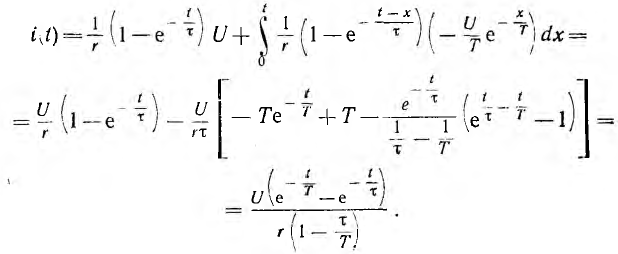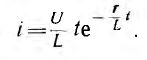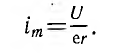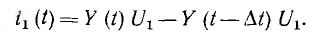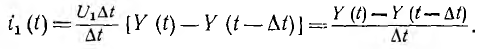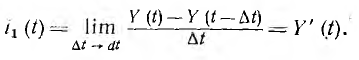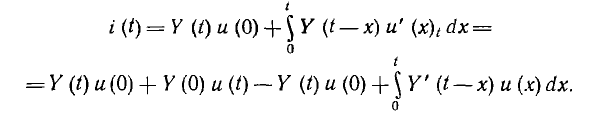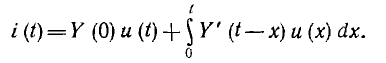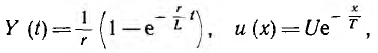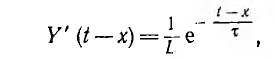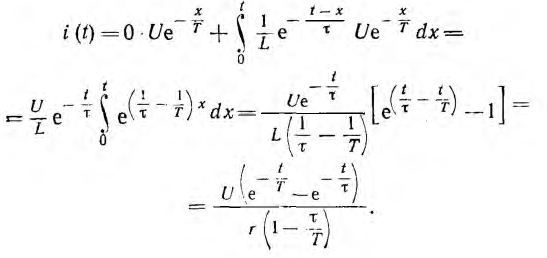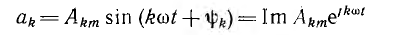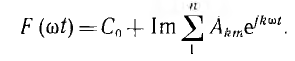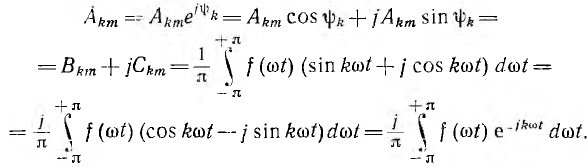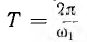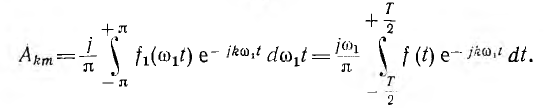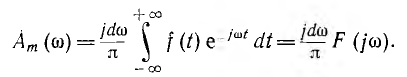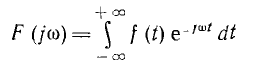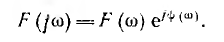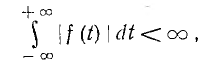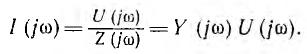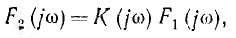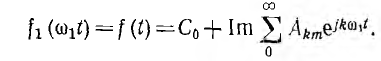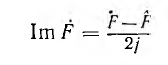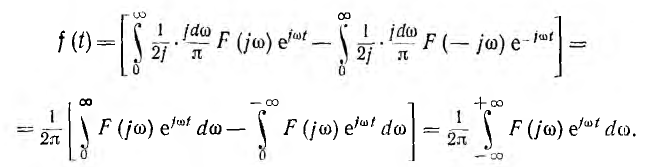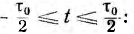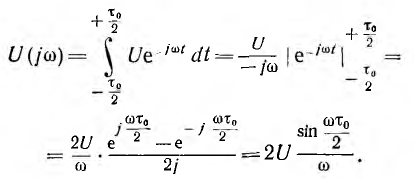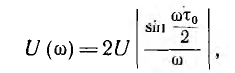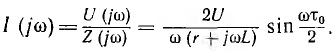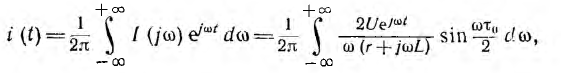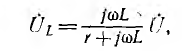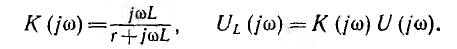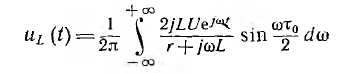Спектральный метод решения дифференциальных уравнений (2 видео)

Спектральный метод

Спектральные методы — это класс техник, используемых в прикладной математике для численного решения некоторых дифференциальных уравнений, возможно, вовлекая Быстрое преобразование Фурье. Идея заключается в переписи решения дифференциальных уравнений как суммы некоторых «базисных функций» (например, как ряды Фурье являются суммой синусоид), а затем выбрать коэффициенты в сумме, чтобы удовлетворить дифференциальному уравнению, насколько это возможно.

Спектральные методы и методы конечных элементов тесно связаны и построены на тех же идеях. Основное отличие заключается в том, что спектральные методы используют базисные функции, ненулевые над всей областью определения, в то время как методы конечных элементов используют базисные функции, которые не равны нулю только на маленьких подобластях. Другими словами, спектральные методы предпринимают глобальный подход, в то время как методы конечных элементов используют локальный подход. Отчасти по этой причине спектральные методы имеют превосходные свойства так называемой «экспоненциальной сходимости», которая наиболее быстрая из возможных, если решение является гладким. Однако не известно трёхмерного однообластного спектрального метода скозного счёта (ударная волна не гладкая). Метод конечных элементов, в котором степень элементов очень высока или возрастает при уменьшении параметра решётки h, иногда называется методом спектрального элемента.

Спектральные методы могут быть использованы для решения обыкновенных дифференциальных уравнений (ОДУ), дифференциальных уравнений в частных производных и задач нахождения собственных значений, вовлекающих дифференциальные уравнения. Когда спектральные методы применяются к зависимым от времени дифференциальным уравнениям в частных производных, решение обычно записывается как сумма базисных функций с зависящими от времени коэффициентами. Подстановка такой суммы в дифференциальное уравнение в частных производных даёт систему обыкновенных дифференциальных уравнений от коэффициентов, которая может быть решена с помощью любого численного метода обыкновенных дифференциальных уравнений. Задача нахождения собственных значений для обыкновенных дифференциальных уравнений аналогичным образом сводится к задаче нахождения собственных значений матрицы.

Спектральные методы были разработаны в длинной серии статей Стивеном Орсага, начиная с 1969 года для методов Фурье для периодических геометрических задач, полиномиальных спектральных методов для конечных и неограниченных геометрических задач, псевдоспектральных методов для сильно нелинейных задач, спектральных итерационных методов для решения задач стационарного состояния и других задач. Имплементация спектрального метода обычно завершается либо коллокацией, либо методом Галёркина, либо Тау-подходом.

Спектральные методы вычислительно менее затратны, чем методы конечных элементов, но становятся менее точными для задач со сложными геометриями и прерывистыми коэффициентами. Это увеличение ошибки является следствием явления Гиббса.

Содержание

Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Спектральный метод на примере простых задач матфизики
Одномерная задача распространения тепла по стержню
Двумерное уравнение диффузии
Двумерное волновое уравнение
Выводы
Расчет переходных процессов
Импульсный интеграл Дюамеля
Область применения метода наложения
Спектральный метод
Пример применения спектрального метода
Область применения спектрального метода
Операторный метод
🔥 Видео

Связанные понятия

В настоящее время отсутствует единое определение точно решаемой задачи для всех разделов математики. Это обусловлено особенностями самих задач и методов поиска их решения. Вместе с тем базовые теоремы, определяющие наличие и единственность решений, строятся на общих принципах, что будет показано ниже.

Точное нахождение первообразной (или интеграла) произвольных функций — процедура более сложная, чем «дифференцирование», то есть нахождение производной. Зачастую, выразить интеграл в элементарных функциях невозможно.

Упоминания в литературе

Связанные понятия (продолжение)

В вычислительной математике одной из наиболее важных задач является создание эффективных и устойчивых алгоритмов нахождения собственных значений матрицы. Эти алгоритмы вычисления собственных значений могут также находить собственные векторы.

Техники спектральной кластеризации используют спектр (собственные значения) матрицы сходства данных для осуществления понижения размерности перед кластеризацией в пространствах меньших размерностей. Матрица сходства подаётся в качестве входа и состоит из количественных оценок относительной схожести каждой пары точек в данных.

О дискретном эквиваленте преобразования Лапласа см. Z-преобразование.В математике дискретный оператор Лапласа — аналог непрерывного оператора Лапласа, определяемого как отношения на графе или дискретной сетке. В случае конечномерного графа (имеющего конечное число вершин и рёбер) дискретный оператор Лапласа имеет более общее название: матрица Лапласа.

В математике и теоретической физике функциональная производная является обобщением производной по направлению. Разница заключается в том, что для последней дифференцирование производится в направлении какого-нибудь вектора, а для первой речь идёт о функции. Оба эти понятия можно рассматривать как обобщение обычного дифференциального исчисления.

Параболические уравнения — класс дифференциальных уравнений в частных производных. Один из видов уравнений, описывающих нестационарные процессы.

Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Спектральный метод на примере простых задач матфизики

В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Одномерная задача распространения тепла по стержню

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:

Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:

Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…

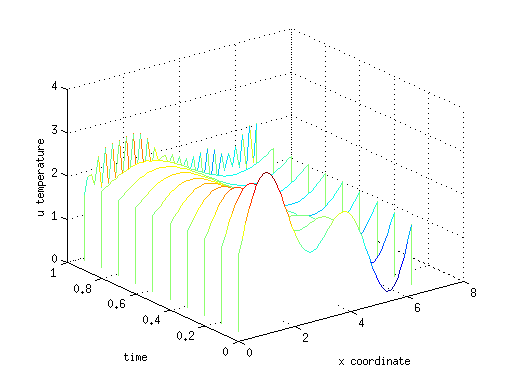
Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает ~~сильные осциляции~~ численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

Двумерное уравнение диффузии

Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):

Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μ_k, зависящий от временного шага и волновых чисел k, т.е. μ_k — это константа, которую не нужно пересчитывать на каждом шаге!

Двумерное волновое уравнение

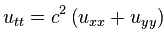
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — u_t, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.

Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы

В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.

Преимуществами метода являются:

Видео:Спектральный анализ вольтерровых интегро-дифференциальных уравненийСкачать

Расчет переходных процессов

Содержание:

Расчет переходных процессов методами наложения, спектральным и операторным:

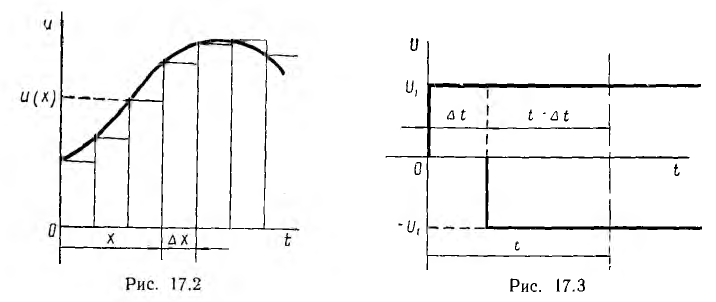
Расчет переходного процесса при включении линейной цепи на напряжение u(t), являющееся любой функцией времени, может быть произведен методом наложения, если заменить кривую напряжения ступенчатой кривой (рис. 17.1). Тогда можно считать, что в момент времени t = 0 цепь включается на постоянное начальное напряжение u(0), а затем на ряд смещенных на равные промежутки времени

Ток или напряжение любой ветви при переходном процессе можнo найти из суммы токов, вызываемых отдельными постоянными составляющими напряжения. Для применения этого метода необходимo предварительно рассчитать переходный ток или напряжение исследуемой ветви цепи по заданному постоянному входному напряжению U₀ или току I₀ и найти зависимую от времени переходную функцию К(t), связывающую искомую и заданную величины Например, при включении цепи г, L на постоянное напряжение ток

Следовательно, переходная функция

В данном случае она имеет размерность проводимости и называется переходной проводимостью

где 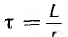постоянная времени этой цепи.

Для постоянного напряжения, включенного позже на время х, переходная проводимость

Аналогичным образом определяется любая переходная функция К (t). Например, напряжение на индуктивности при включении цепи г, L на постоянное напряжение U₀ и переходная функция соответственно равны:

В этом случае переходная функция безразмерна. Переходная функция в принципе сразу определяет выходную величину, так как дает численное значение (но не размерность!) выходной величины, когда входная (U₀ или I₀) равна единице.

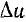
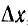
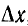
Составляющая переходного тока от напряжения u(0), включаемого в начальный момент, равна У (t) и (0), а от скачка напряжения , включаемого в момент х + , равняется Y (t — х — ). В результате приближенное значение искомого переходного тока будет:

Точное значение тока i (t) получится при переходе 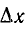в пределе к бесконечно малым промежуткам времени dx. Тогда

и ток

Это выражение называется интегралом Дюамеля. При определении напряжения какой-либо ветви в интеграле Дюамеля вместо переходной проводимости должна стоять соответствующая переходная функция.

Далее в виде примера определен ток при включении цепи г, L на затухающее по показательному закону напряжение 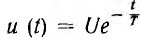, где Т — постоянная времени, характеризующая скорость затухания u(t). Переходные проводимости для этого случая даны выше, a

После подстановки этих величин в интеграл Дюамеля и интегрирования определяется искомый ток:

В частном случае, когда τ= Т, получается неопределенность, которая после раскрытия дает:

Во всех случаях переходный ток положителен и имеет максимум i_m, определяемый обычным образом. При τ = Т

Применение метода наложения удобно также в тех случаях, когда напряжение, на которое включается цепь, представляет собой кусочно-аналитическую кривую, имеющую разрывы. При этом переходный ток определяется как сумма интегралов Дюамеля за время отдельных участков u (t), причем в их первых членах У (t) u (0) напряжение u (0) равно разности приложенных напряжений после и до разрыва, с которого начинается данный участок.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Импульсный интеграл Дюамеля

Метод наложения может быть также применен, если заданное входное напряжение u (t) представить в виде следующих друг за другом прямоугольных импульсов напряжения u (х) малой длительности 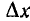(рис. 17.2) с последующим наложением выходной величины, например тока цепи, от каждого импульса напряжения с учетом его величины и сдвига во времени.

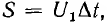
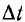
Прямоугольный импульс (рис. 17.3) характеризуется интенсивностью равной произведению амплитуды импульса U₁ на его длительность . Импульс с интенсивностью S = I называется единичным.

Один прямоугольный импульс может быть представлен алгебраической суммой двух одинаковых скачков постоянного напряжения +U_l и —U₁ из которых второй возникает на время 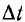позже первого. Тогда ток i₁(t) от рассматриваемого импульса напряжения в момент t определяется с помощью переходной проводимости, которая для первого скачка равна У(t) а для второго

Если на цепь воздействует единичный импульс напряжения, т. е. 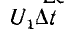= 1, предыдущее выражение получает вид:

При переходе к пределу единичный импульс превращается в так называемую единичную импульсную функцию, а ток

Таким образом, аналогично численному равенству переходной проводимости Y (t) току от единичного скачка напряжения, при единичной импульсной функции напряжения ток равен производной от Y (t). Поэтому Y'(t) называется импульсной переходной проводимостью.

Для установления связи между искомым током i (t), заданным напряжением произвольной формы, разбитым на элементарные импульсы u (х), и импульсной переходной проводимостью, можно идти тем же путем, как и при выводе интеграла Дюамеля, но проще это сделать, интегрируя его по частям:

Отсюда получается импульсный интеграл Дюамеля:

В общем случае в импульсный интеграл Дюамеля вместо u (х) следует подставить заданную входную величину, а взамен Y’ (t — х) — соответствующую импульсную переходную функцию К’ (t — х).

Далее в виде примера решается та же задача — определение переходного тока i (t) при включении цепи г, L на напряжение u (t) = 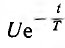. Здесь

Y’ (t — x) есть производная функции Y (t — x) по ее аргументу t — x, или, что то же самое, ее производная по t:

где 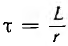— постоянная времени цепи. Из-за наличия индуктивности Y (0) = 0, ток

Таким образом получен тот же результат, что и при применении первой формы интеграла Дюамеля, но вычисления в данном примере несколько упростились.

Видео:Поле направлений дифференциального уравнения первого порядкаСкачать

Область применения метода наложения

Из изложенного видно, что метод наложения позволяет найти выходную величину переходного процесса по заданной или полученной путем аппроксимации аналитической зависимости входной величины от времени. При этом следует применять ту форму интеграла Дюамеля, для которой подынтегральное выражение упрощается. Очевидно, что метод наложения применим только в случае интегрируемых функций.

Спектральный метод

Прямое н обратное преобразование Фурье:

Для расчета переходных процессов при включении цепи на непериодическое напряжение было применено его разложение на скачкообразные или импульсные напряжения с последующим применением принципа наложения. Эту задачу также можно решить, если представить непериодическую функцию в виде суммы гармоник.

Так как каждая гармоника ряда Фурье может быть записана в комплексной форме:

(А_кm — комплексная амплитуда), весь ряд Фурье может быть также записан в комплексной форме:

Коэффициенты этого ряда, т. е. комплексные амплитуды гармоник, могут быть определены из данных выражений для В_кm и С_кm—

Комплексная амплитуда гармоники k периодической функции 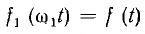с периодом

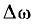
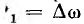
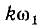
Непериодическую функцию можно рассматривать как предельный лучай периодической, у которой период Т стремится к бесконечности. Тогда разница в частоте между двумя соседними гармониками будет стремиться к dω. Так как частота основной (первой) гармоники , она также стремится к dω. Частота гармоники k должна быть обозначена через ω. Тогда общее выражение комплексной амплитуды гармоники частоты ω получает вид:

Таким образом, воздействие на цепь непериодической функции i(t) может быть заменено суммарным воздействием бесконечно большого числа бесконечно малых гармоник, т. е. спектра А_m (ω). Относительное значение амплитуд гармоник пропорционально комплексной функции частоты F (jV), имеющей вид интеграла Фурье:

и называемой спектральной характеристикой или спектральной плотностью функции f(t). Эта характеристика может быть записана в показательной форме:

Тогда F (ω) называется амплитудно-частотной, а 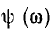— фазо-частотной характеристикой.

Преобразование f (t) в F (jω), т. е. прямое преобразование Фурье, возможно, если интеграл Фурье имеет конечное значение. Так как 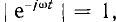, для этого достаточно, чтобы интеграл

чего, например, не будет, если f (t) — постоянная величина или синусоидальная функция.

Первым этапом спектрального метода расчета переходных процессов является преобразование оригинала f(t) в его изображение F (jω). Если U (jω) является спектральной характеристикой напряжения, спектральная характеристика тока I (jω) может быть найдена из закона Ома по известному комплексному сопротивлению Z (jω) или проводимости Y (jω) цепи, в общем случае являющимися также комплексными функциями частоты. Тогда

В общем случае при задании какой-либо функции с характеристикой F₁ (jω), воздействующей на вход цепи, характеристика искомой функции выхода

где К (jω) — так называемая передаточная функция. При изменении частоты со передаточная функция изменяется и по вели чине и по фазе. В отличие от аналогичной величины — переходно функции, которая характеризовала переходный процесс при воздействии на цепь постоянного напряжения, передаточная функция К (jω) характеризует установившийся процесс при синусоидальном воздействии.

После определения спектральной характеристики, т. е. изображения искомой величины, должен быть найден оригинал. Для вывод формулы обратного преобразования F (jω) в f (t) может быть такж использован переход от дискретного ряда к непрерывному.

Ряд Фурье в комплексной форме имеет вид:

Учитывая, что мнимая часть любого комплексного числа F

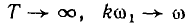
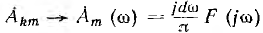
(F— сопряженный комплекс), после переходов и получают следующее значение непериодической функции:

Постоянная составляющая (ω = 0) учтена тем, что нижний предел исходных интегралов взят равным нулю.

Это обратное преобразование Фурье служит для получения искомой функции времени по ее спектральной характеристике.

Необходимо отметить, что отрицательная частота имеет лишь математический смысл. Она возникла в результате замены синусоид показательными функциями .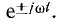

Пример применения спектрального метода

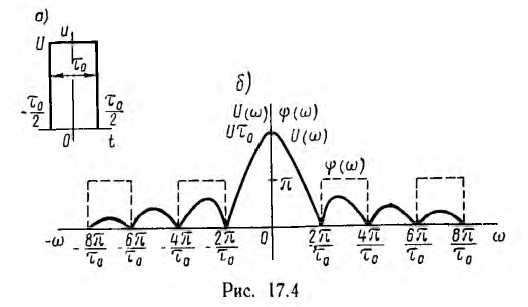
В качестве примера рассматривается переходный процесс включения цепи г, L на прямоугольный импульс напряжения U продолжительностью т₀. После окончания импульса контур остается замкнутым.

Для упрощения удобно представить импульс существующим с момента времени 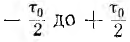(рис. 17.4, о). Так как вне этого промежутка времени f (t) = 0, интеграл Фурье вычисляется только для

Это и есть спектральная плотность, которая в данном случае вещественна и изображается вектором, совпадающим с осью вещественных.

Счедовательно, фаза спектральной плотности равна нулю, когда дробь 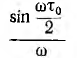— положительна, и равна π, когда эта дробь отрицательна. Амплитудно-частотная характеристика, очевидно, равна:

откуда U (0) = 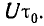. Амплитудно-частотная и фазо-частотная характеристика изображены на рис. 17.4, б.

Так как сопротивление цепи 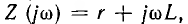, спектральная характеристика тока

Переходный ток находят с помощью обратного преобразования Фурье:

что требует вычисления интеграла сравнительно сложной функции Решение этой же задачи методом наложения (включение цепи на напряженние U при t = 0 и на — U при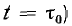значительно проще.

Если требуется найти напряжение u_L (t) на индуктивности, то, та как

передаточная К (jω) и спектральная U_L(jω) функции получают вид,

Определение искомого напряжения

также связано с вычислением интеграла.

Область применения спектрального метода

Как видно из изложенного, непосредственное применение спектрального метода имеет следующие ограничения:

он может применяться только для абсолютно интегрируемых функций;
этот метод принципиально не учитывает начальных условий, поэтому он применим только для задач с нулевыми начальными условиями.

Некоторые искусственные приемы позволяют обойти эти ограничения, но при этом расчеты еще больше усложняются. Как было видно из рассмотренного примера, наиболее трудным этапом является обратное преобразование, связанное с интегрированием сложных функций. В ряде случаев интегралы не берутся и приходится прибегать к приближенным расчетам. Очевидно также, что спектральный метод как разновидность метода наложения применим только для линейных цепей.

Ценность спектрального метода заключается в том, что расчет переходных процессов сводится к расчету установившихся режимов в цепях синусоидального тока и, следовательно, к возможности получения ответа без составления и решения дифференциальных уравнений. Задачи могут быть решены при помощи определенных из опыта или заданных аналитически или графически амплитудно-частотных харак теристик входных напряжений и токов цепи и передаточных функций Этот метод в чистом или приближенном виде широко применяется в тео рии автоматического регулирования и радиотехнике.

Операторный метод

Прямое и обратное преобразования Лапласа:

Пусть функция f (t), равная нулю при t

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.