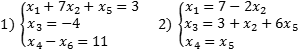Совпадают ли множества решений систем уравнений (7 видео)

Содержание

Критерий совместности систем линейных уравнений
Системы линейных уравнений: основные понятия
22. Связь решений однородной и неоднородной систем линейных уравнений
🔍 Видео

Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Критерий совместности систем линейных уравнений

Тема 2. Системы линейных уравнений

Критерий совместности систем линейных уравнений

Система m линейных уравнений c n неизвестными имеет вид:

(2.1)

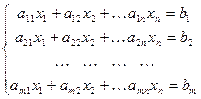
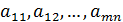
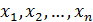
Здесь – коэффициенты системы, – свободные члены, а — неизвестные вещественные числа. Используя понятие произведения матриц, можно переписать систему (2.1) в матричном виде:

где A = (а_ij) — матрица, состоящая из коэффициентов при неизвестных системы (2.1), которая называется матрицей системы, X = (x₁, x₂. x_n) T ,
B = (b₁, b₂. b_m) T — векторы-столбцы, составленные соответственно из неизвестных x_j и из свободных членов b_i.

Система называется однородной, если все ее свободные члены равны нулю: b_i=0 для всех i.

Если хотя бы один из свободных членов отличен от нуля, система называется неоднородной.

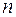
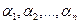
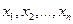
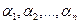
Совокупность чисел называется решениемсистемы (2.1), если после замены неизвестных числами соответственно каждое из уравнений системы превращается в верное равенство

Система (2.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

= ,

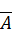
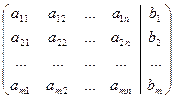
образованная путем приписывания справа к матрице 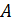столбца свободных членов, называется расширенной матрицей системы.

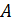
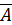
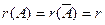
Теорема Кронекера- Капелли. Система линейных уравнений (2.1) совместна тогда и только тогда, когда ранги матриц и совпадают, т.е.
.

Для множества решений системы (2.1) имеются три возможности:

1) Если 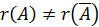, решений нет. В этом случае система несовместна.

2) Если 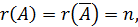cистема имеет единственное решение. В этом случае система называется определенной.

3) Если 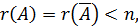cистема имеет бесчисленное множество решений. В этом случае система называется неопределенной.

Рассмотрим более подробно случай неопределенной системы. Предположим, что базисный минор матрицы находится в левом верхнем углу расширенной матрицы (всегда можно перенумеровать неизвестные и поменять местами строки, чтобы это было верно). Если ранг расширенной матрицы системы равен r, то первые r ее строк являются базисными. По теореме о базисном миноре каждая из строк расширенной матрицы, начиная с (r+1)-ой строки, является линейной комбинацией первых r строк этой матрицы. Это означает, что каждое из уравнений системы (2.1), начиная с (r+1)-го уравнения, является линейной комбинацией первых r уравнений этой системы. 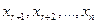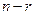Придавая неизвестным совершенно произвольные значения, достаточно найти r неизвестных из первых r уравнений системы. Таким образом, в случае неопределенной системы переменных, которые называются базисными переменными, выражаются через ( ) переменных, которые называются свободными переменными.

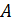
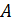
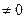
Универсальным методом решения систем линейных уравнений является метод Гаусса, или метод исключения неизвестных. В частном случае, когда матрица системы квадратная и ее определитель отличен от нуля det( ) , можно использовать для нахождения решения либо метод Крамера, либо матричный метод.

Пример 2.1. Исследовать систему уравнений на совместность:

Решение.Выписываем расширенную матрицу системы:

= .

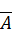
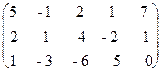
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 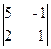= 7 ¹ 0; содержащие его миноры третьего порядка равны нулю:

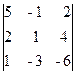
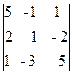
M¢₃ = = 0, M²₃ = = 0.

Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы `A рассмотрим окаймляющий минор

= = -35 ¹ 0,

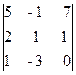
значит, ранг расширенной матрицы r( 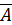) = 3. Поскольку r(A) ¹ r( ), то система несовместна.

Дата добавления: 2015-09-29 ; просмотров: 3031 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Системы линейных уравнений: основные понятия

— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

— это последовательность чисел ( k ₁, k ₂, . k_n ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x ₁, x ₂, . x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

Переменная x_i называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x_i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x ₁, x ₃ и x ₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x ₁, x ₃ и x ₅. Достаточно переписать самое последнее уравнение в виде x ₅ = x ₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x ₁ = b ₁, x ₂ = b ₂, . x_k = b_k ;
Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x ₂, x ₅, x ₆ (для первой системы) и x ₂, x ₅ (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.

Теорема. Если в системе из n уравнений переменные x ₁, x ₂, . x_r — разрешенные, а x _{r + 1}, x _{r + 2}, . x _k — свободные, то:

Если задать значения свободным переменным ( x _{r + 1} = t _{r + 1}, x _{r + 2} = t _{r + 2}, . x_k = t_k ), а затем найти значения x ₁, x ₂, . x_r , получим одно из решений.
Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.

Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

22. Связь решений однородной и неоднородной систем линейных уравнений

Пусть (25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется Соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам:

(30)

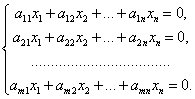
10. Сумма решений данной неоднородной и соответствующей однородной системы линейных уравнений есть решение данной неоднородной системы. Пусть А – частное решение системы (25) и С – частное решение системы (30). Рассмотрим вектор (А + С).

20. Разность двух решений неоднородной системы линейных уравнений есть решение соответствующей однородной системы.

30. Если А – фиксированное частное решение системы (25), а С пробегает все решения системы (30), то (А + С) пробегает все решения системы (25).

Согласно 10, при любом С Вектор (А + С) будет решением системы (25). Если D – любое решение системы (25), то, согласно 20, разность (D – А) будет решением системы (30). Обозначив (D – А) = С, получим D = (А + С).

Теорема 29. Если А – частное решение линейной неоднородной системы уравнений и А1, а2, …, аn–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид

(Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.)

Доказательство Является следствием предыдущих свойств.