Совокупность уравнений и их решение (2 видео)

Совокупности уравнений, неравенств, систем и т.п.

Вообще в школьных учебниках алгебры о совокупностях информации очень мало. Про совокупности упоминается лишь вскользь, да и то в старших классах. С нашей точки зрения это не очень справедливо хотя бы потому, что использование совокупностей довольно удобно при оформлении решений уравнений, неравенств и их систем. Давайте восполним этот пробел.

Ниже представлен материал, дающий общее представление о совокупностях уравнений, неравенств, систем и их всевозможных комбинаций. Здесь вы найдете определения совокупностей и их решений, принятые обозначения, а также поясняющие примеры.

Навигация по странице.

Содержание

Что такое совокупность уравнений, неравенств, систем?
Что называется решением совокупности?
Совокупность уравнений и неравенств
Совокупность уравнений (неравенств) – это несколько неравенств или уравнений, решения которых нужно объединить.
Совокупности уравнений, неравенств, систем: определение, как решить
Понятие совокупности
Что такое решение совокупности
🔍 Видео

Видео:СИСТЕМА И СОВОКУПНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Что такое совокупность уравнений, неравенств, систем?

Сразу скажем, что если у Вас сформировано четкое представление о системах уравнений и системах неравенств, то определения совокупностей воспримутся очень легко. Прочитав их, Вы сразу почувствуете, будто уже их встречали.

Информация из учебников [1, с. 24; 2, с. 129; 3, с. 64-65] позволяет записать следующее определение совокупности уравнений:

Совокупностями уравнений называются записи, представляющие собой несколько расположенных друг под другом уравнений, которые слева объединены квадратной скобкой, и обозначающие множество всех таких решений, которые являются решениями хотя бы одного из уравнений совокупности.

Давайте проведем параллель между системами и совокупностями. Системы записывают с помощью фигурной скобки, а совокупности – с помощью квадратной, системы обозначают множество решений, которые являются решениями каждого уравнения системы, а совокупности – множество решений, которые являются решениями хотя бы одного уравнения совокупности.

Для наглядности приведем примеры совокупностей уравнений: , .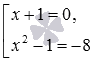

Здесь заметим, что в школе при записи совокупностей часто не используют квадратную скобку, а просто перечисляют через запятую составляющие этой совокупности. Так последняя совокупность из предыдущего абзаца может быть записана как x+y 2 +z 4 =0 , x·y·z=0 , z=5 .

Аналогично определяется и совокупность неравенств:

Совокупность неравенств – это запись, представляющая собой несколько записанных одно под другим неравенств, объединенных слева квадратной скобкой, и обозначающая множество решений, являющихся решениями хотя бы одного из неравенств совокупности.

Это определение находится в согласии с описанием совокупностей неравенств, приведенным в учебнике Мордковича [1, с. 222] .

Вот пример совокупности неравенств .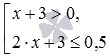

При описании совокупностей при надобности можно уточнять число составляющих их уравнений и неравенств, число переменных и вид уравнений и неравенств. К примеру, совокупность из предыдущего абзаца – это совокупность двух неравенств с одной переменной x , причем составляющие ее неравенства – целые рациональные первой степени.

Под знак совокупности можно поместить не только уравнения или неравенства по отдельности. Есть смысл рассматривать, например, совокупность уравнения и двух неравенств, неравенства и системы уравнений, совокупность двух систем неравенств и т.п. При этом главное сохранять смысл, заключающийся в совокупности, — она означает множество решений, являющихся решением хотя бы одного объекта совокупности.

Для примера приведем совокупность двух систем неравенств и совокупность такого вида .

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Что называется решением совокупности?

К совокупностям непосредственно относятся их решения. Дадим определения решений совокупностей с одной переменной, а также с двумя, тремя и большим числом переменных.

Решением совокупности с одной переменной называется такое значение переменной, которое является решением хотя бы одного составляющего элемента совокупности.

Например, если речь идет о совокупности уравнений с одной переменной, то решение совокупности – это значение переменной, которое является решением хотя бы одного составляющего ее уравнения. Так x=3 – это решение совокупности неравенств , так как 3 является решением первого неравенства. А вот нуль не является решением записанной совокупности, так как это значение не является решением ни одного неравенства совокупности, действительно, 0>1 и 0 2 ≥4·0+2 – неверные числовые неравенства.

Решением совокупности с двумя, тремя и большим числом переменных называется двойка, тройка и т.д. значений переменных, являющаяся решением хотя бы одного объекта совокупности.

В качестве примера рассмотрим следующую совокупность . Пара значений (3, 0) есть решение этой совокупности, так как она является решением системы , потому что 3+0>0 и 3≥3 — верные неравенства. А пара значений x=−1 , y=2 не является решением совокупности, так как она не является решением ни уравнения x 2 +y 2 =4 , ни системы неравенств .

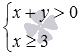
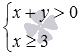
Иногда используются термины «частное решение совокупности» и «общее решение совокупности». Под частным решением совокупности понимают одно отдельно взятое решение, а общим решением называют множество всех частных решений совокупности. Но чаще говорят просто о решении совокупности, а уже из контекста черпают дополнительную информацию, о частном или об общем решении идет речь.

В заключение заметим, что из определения совокупности и ее решений следует такой вывод: решение совокупности есть объединение решений всех элементов, составляющих совокупность. А решение систем, напомним, есть пересечение решений всех ее элементов.

Продолжить изучение темы рекомендуем материалом статьи равносильные совокупности.

Видео:9 класс, 4 урок, Совокупности неравенствСкачать

Совокупность уравнений и неравенств

Совокупность уравнений (неравенств) – это несколько неравенств или уравнений, решения которых нужно объединить.

Совокупность выглядит вот так:

Совокупности похожи на системы – в них так же присутствуют два или более неравенства (уравнения), но в отличие от системы мы ищем решение, которое подходит хотя бы одному из них (а не всем сразу).

Давайте сравним решение системы и совокупности:

(begin2x-8>0\fracx≤3,5end)

( left[ begin2x-8>0\ fracx≤3,5endright.)

Сначала в обоих случаях нужно решить каждое неравенство и нанести решения на числовую ось.

(begin2x>8 ; \|:4\fracx≤3,5 ;;; \|cdot 2 end)	( left[ begin2x>8 ; ;\|:4\ fracx≤3,5 ;;; \|cdot 2endright.)
(beginx>4\x≤7 end)	( left[ beginx>4\ x≤7 endright.)

Ответ: ((4;7])	Ответ: ((-∞;+∞))

То есть решение неравенств внутри системы и совокупности одинаково. Но разница появляется, когда мы начинаем искать окончательный ответ. В случае с системой мы «пересекаем» решения: т.е. ищем иксы, которые подходят и первому, и второму неравенству. А в случае с совокупностью мы «объединяем» решения, то есть находим иксы, которые подходят хотя бы одному неравенству (или обоим сразу).

Наглядно эту идею можно представить так:

решение системы решение совокупности

В первом перенесем (-5) в правую часть, а во втором – вынесем за скобку икс.

( left[ beginfrac>6\ x(x-7) 18\ x(x-7) квадратные с одной переменной. Решая их по отдельности (через дискриминант или по теореме Виета – неважно), находим корни:
— у первого уравнения корни: (-3) и (1);
— у второго уравнения корни: (-3) и (7).
А окончательным ответом будут они все, то есть:

Замечание: если бы мы в последнем примере решали не совокупность, а систему, то в ответ пошло бы только одно значение: (-3) (потому что только оно подходит обоим уравнениям сразу).

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Совокупности уравнений, неравенств, систем: определение, как решить

Тема совокупностей уравнений и др. систем, как правило, в рамках школьного курса представлена скупо. В 10-11 классе она изучается совсем недолго. Мы считаем, что это неверный подход, поскольку совокупности — прекрасный способ оформления привычных решений при работе с неравенствами и уравнениями, поэтому в рамках статьи мы раскроем этот вопрос.

В данной статье мы сформулируем общее понятие совокупностей неравенств, уравнений и их систем, а также их комбинации. Кроме определений здесь, как обычно, есть решения задач, наглядно поясняющие тот или иной фрагмент текста.

Видео:Система и совокупность. Как решать неравенстваСкачать

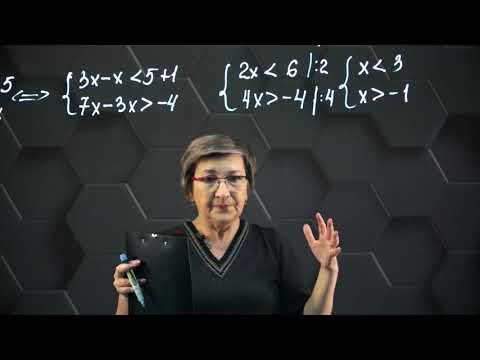
Понятие совокупности

Для того, чтобы хорошо понимать, что такое совокупность уравнений, нужно вспомнить еще одно понятие из школьного курса алгебры — система уравнений (аналогично неравенствам). Тогда определения совокупности покажутся вам знакомыми и легко усвоятся.

Проанализировав несколько учебников, выберем наиболее удачное определение:

Совокупность уравнений представляет собой несколько уравнений, записанных друг под другом и объединенных квадратной скобкой. Значение этой записи таково: совокупность объединяет такие значения переменных, при которых хотя бы одно из входящих в нее уравнений превращается в верное равенство.

Сравним между собой понятие совокупности и понятие системы:

Запись совокупности, как мы уже говорили выше, осуществляется с помощью квадратной скобки, а системы записываются с фигурной.
Совокупность включает в себя множество решений, которые относятся хотя бы одному из уравнений, входящих в ее состав. Система объединяет решения, которые подходят для каждого уравнения.

Пример 1

Вот примеры совокупности уравнений:

x + 1 = 0 , x 2 — 1 = — 8 x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5

Иногда при записи совокупности можно обойтись и без квадратной скобки: так часто делают в школе. В таком случае уравнения можно просто указать через запятую. Для примера выше это может быть запись вида x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5 .

Понятие совокупности неравенств формулируется схожим образом.

Совокупность неравенств представляет собой несколько неравенств, записанных друг под другом и объединенных квадратной скобкой. Она включает в себя решения, которые подходят хотя бы для одного из неравенств, входящих в состав совокупности.

Приведем пример такой записи:

x + 3 > 0 , 2 · x + 3 ≤ 0 , 5

Схожее определение для этого понятия упоминается в учебнике Мордковича.

Если необходимо, то можно указать, сколько уравнений (неравенств) входят в состав совокупности, а также сколько в ней участвует переменных. Вид уравнения (неравенства) также может быть внесен в запись при необходимости. Сформулируем название совокупности из примера: это совокупность 2-х неравенств с одной переменной, а ее составные части — это целые рациональные первой степени.

Сочетать в рамках одной совокупности можно не только записи одного вида. Так, имеет право на существование совокупность, состоящая из двух неравенств и одного уравнения, сочетание одного неравенства с системой уравнений, двух систем неравенств и др. Главная задача — сохранить неизменным основной смысл совокупности: в нее входят такие решения, которые подходят хотя бы для одной составляющей совокупности.

В качестве примера смешанных совокупностей приведем две:

x > 3 x 8 x — 5 x ≤ — 2 x 2 = 9 x 2 > 5 ( x — 6 ) · ( x — 8 ) = 0 x ≤ 3 x 2 + 2 · x — 8 > 0

Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать

Что такое решение совокупности

Решение — главная составляющая совокупности. Сформулируем, что же такое решения совокупности с разным количеством переменных.

Решение совокупности с одной переменной представляет собой значение этой переменной, которое является решением хотя бы одной составляющей совокупности (уравнения, неравенства).

Если мы возьмем совокупность уравнений, значит, его решение — это значение x , при котором хотя бы одно из уравнений, входящих в состав совокупности, обращается в верное равенство.

Возьмем неравенство x > 1 , x 2 ≥ 4 · x + 2 . Для него решением, например, будет тройка, т.к. она больше единицы, и, следовательно, она — верное решение для первого неравенства. А если мы возьмем ноль, то увидим, что ни к одному из неравенств он не подходит; значит, 0 в качестве решения совокупности мы рассматривать не можем , ведь запись вида 0 > 1 и x 2 ≥ 4 · x + 2 неверна.

Решение совокупности, в которую входит две, три и более переменных, — это две, три и более переменных, которые подходят в качестве решения хотя бы одному компоненту совокупности.

Возьмем еще один пример, посложнее. У нас есть совокупность:

x 2 + y 2 = 4 , x + y > 0 , x ≥ 3

Значения 3 и 0 будут верными решениями совокупности: они подходят в качестве верных значений в уравнения 2 и 3 ( 3 + 0 > 0 и 3 ≥ 3 — верно). А вот значения 2 и 1 не есть решение совокупности: ни к 1 , ни ко 2 , ни к 3 они не подойдут.

В некоторых учебниках можно встретить также понятия общего и частного решения совокупности; под частным при этом понимается одно решение, а под общим — их некое множество. Но более употребительно понятие просто решения совокупности, а о том, общее оно или частное, можно понять из контекста.

Также нужно отметить следующее: объединение решений всех компонентов совокупности также есть решение совокупности. Напомним, что решение системы представляет собой пересечение решений ее компонентов.

В продолжение темы мы советуем вам материал «Равносильные совокупности».