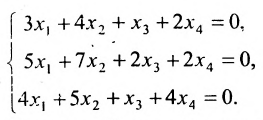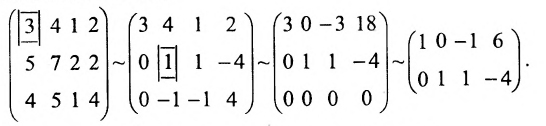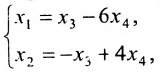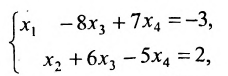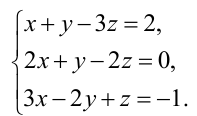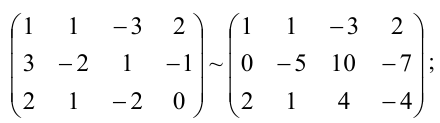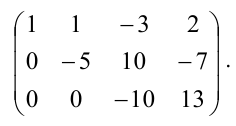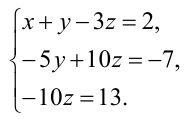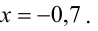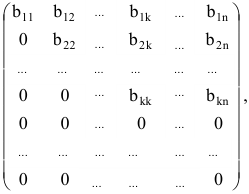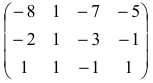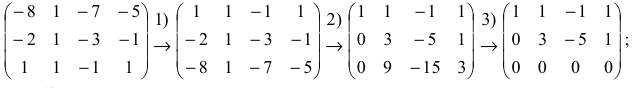Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
. Решением этой системы является любая пара чисел, отличающихся знаком.
- И третий случай, когда система вообще не имеет решения. Например,
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы 
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: 
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.
Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

Таким образом, x = 3, y = – 1.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А -1 .
Решите матричное уравнение AX+B=C, где
Из уравнения получаем 
Следовательно,
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и 
Наконец несложно заметить, что
Таким образом, получаем равенство: 
Следовательно, 
Аналогично выводятся равенства 

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.


- При
- При p = 30 получаем систему уравнений
которая не имеет решений.
- При p = –30 система принимает вид
и, следовательно, имеет бесконечное множество решений x=y,y Î R.
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 

Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
- перестановка строк или столбцов;
- умножение строки на число, отличное от нуля;
- прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
- Метод Гаусса — определение и вычисление с примерами решения
- Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
- Исследование совместности и определённости системы. Теорема Кронекера-Капелли
- Однородные системы линейных уравнений
- Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
- Определение метода Гаусса
- Вычисление метода Гаусса
- Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
- Способ №1. Вычисление рангов по определению.
- Способ №2. Вычисление ранга методом элементарных преобразований.
- 🎥 Видео
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Метод Гаусса — определение и вычисление с примерами решения
Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)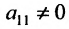
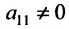
На первом шаге метода Гаусса исключим неизвестное 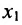
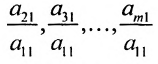
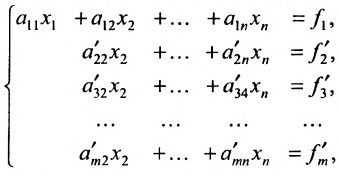
в которой коэффициенты 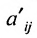
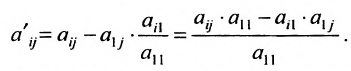
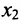
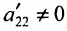
чтобы это условие было выполнено). Для исключения неизвестного 
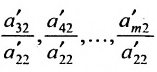
в которой коэффициенты 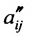
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
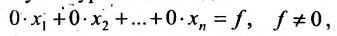
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 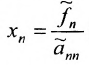
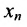
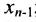
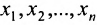
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного 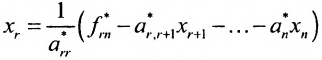
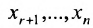
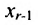
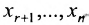
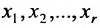
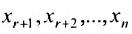
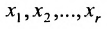
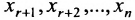
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 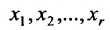
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности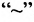
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 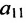
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 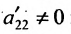
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 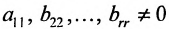
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
Система имеет единственное,решение 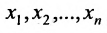
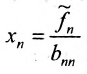
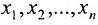
5.2. 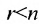
Тогда r неизвестных будут базисными, а остальные (n-r) — свободными. Из последнего уравнения выражаете неизвестное 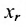
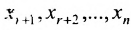
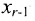
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
— разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 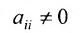
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 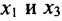
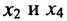
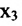
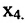
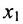
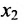
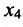
в котором 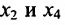
Если в общем решении положить 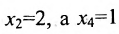
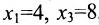
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 
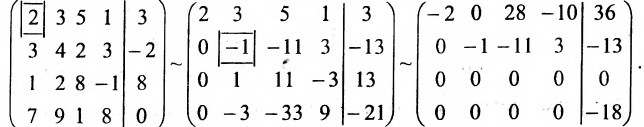
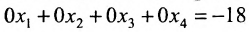
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 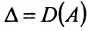
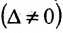
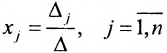
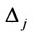
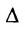
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 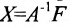
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа — единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева — единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
то обратная матрица 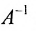
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 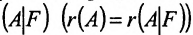
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 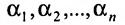
Из этих равенств следует, что последний столбец матрицы 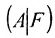
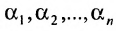
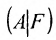
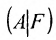
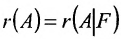
Достаточность. Пусть 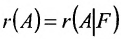
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 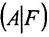
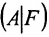
где 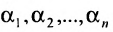
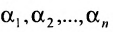
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 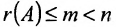
В случае 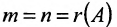
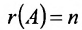
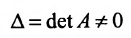
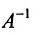
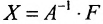
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 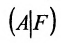
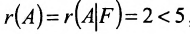
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 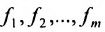
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r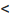
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 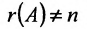
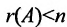
Достаточность. Если 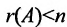
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию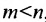
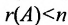
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 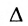
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
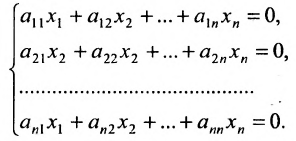
Если определитель матрицы системы 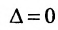
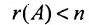
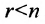
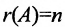
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 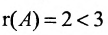
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 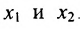
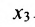
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
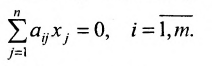
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку 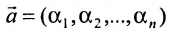
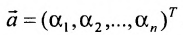
1) сумма двух решений также является решением системы, т.е.
если 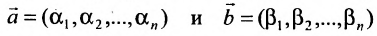
(6.4.1), то и 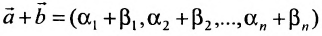
2) произведение решений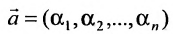
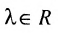
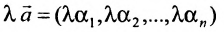
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)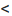
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 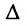
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
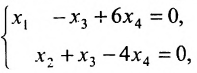
, из которой находим общее решение:
в котором 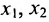
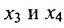
Построим фундаментальную систему решений. Для этого выбираем определитель 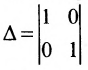
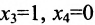
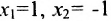
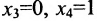
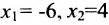
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 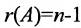
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
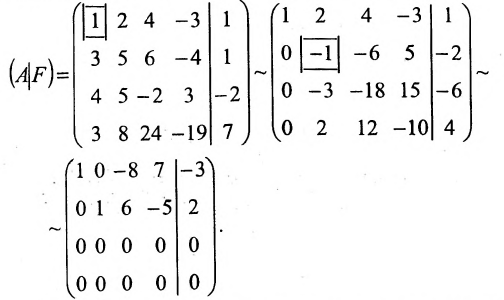
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 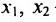
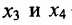
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 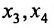
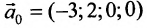
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 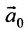
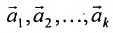
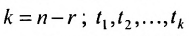
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 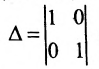
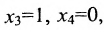
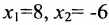
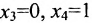
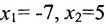
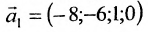
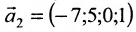
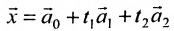
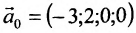
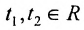
Видео:Решение системы уравнений методом ГауссаСкачать

Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 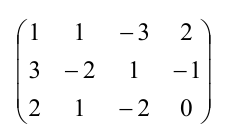
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 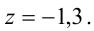
Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 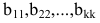
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
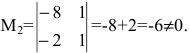
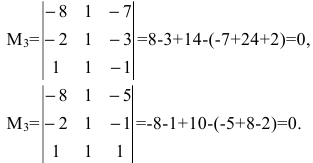
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ left <begin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. endright.$ на совместность. Если СЛАУ совместна, указать количество решений.
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:
Видео:Исследование систем линейных уравнений на совместностьСкачать

Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:
$$ Delta A=left| begin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end right|=-21. $$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
$$ left( begin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end right) begin phantom\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end right) begin phantom\phantom\r_3-r_2\ r_4-r_2\r_5+r_2endrightarrow\ $$ $$ rightarrowleft( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end right) begin phantom\phantom\phantom\ r_4-r_3\phantomendrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right) $$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ left( begin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) overset<r_1leftrightarrow> $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) begin phantom\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end right) begin phantom\ phantom\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end rightarrow $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end right) begin phantom\ phantom\phantom \ r_4-r_3 \ r_5+r_2 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end right) $$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde=ranglt$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
🎥 Видео
Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Неоднородная система линейных уравненийСкачать

Однородная система слау. Тривиальное решение. Ненулевое решениеСкачать

Матричный метод решения систем уравненийСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Решение системы уравнений методом Крамера.Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Базисные решения систем линейных уравнений (01)Скачать

2.1 Системы линейных уравнений IСкачать

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать


 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.





















 которая не имеет решений.
которая не имеет решений. и, следовательно, имеет бесконечное множество решений x=y,y Î R.
и, следовательно, имеет бесконечное множество решений x=y,y Î R.









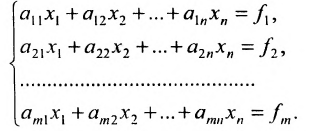
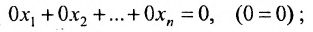
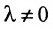 ;
;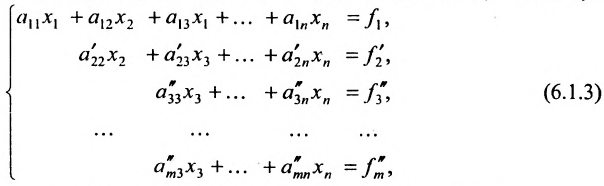
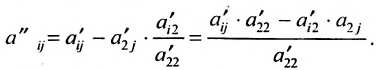
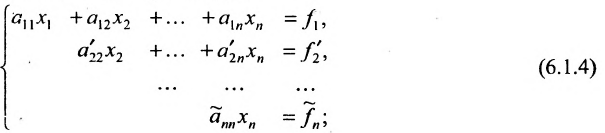
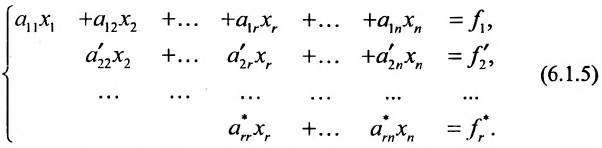

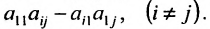
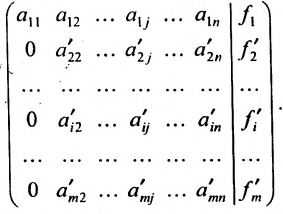
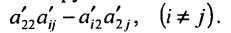

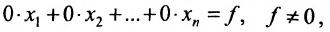
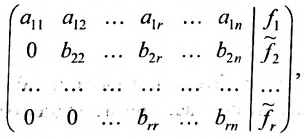
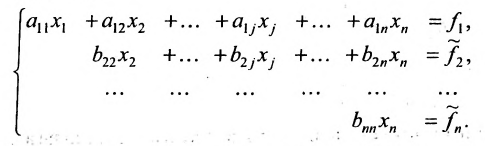
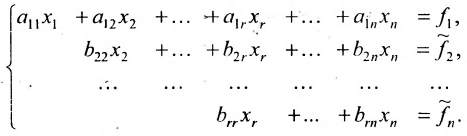
 (если
(если  , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 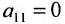 );
);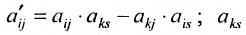 — разрешающий элемент (см. схему).
— разрешающий элемент (см. схему).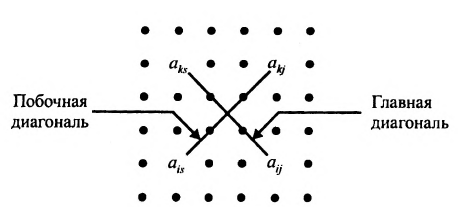
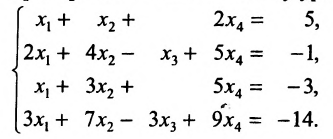


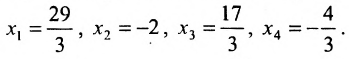
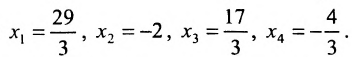
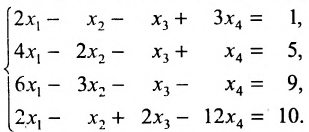

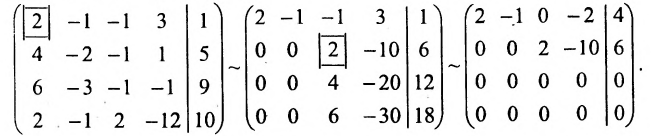

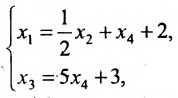
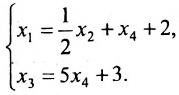
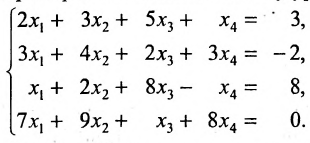
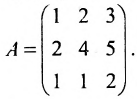
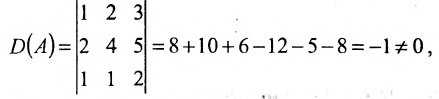

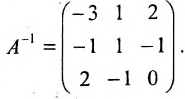
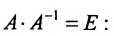
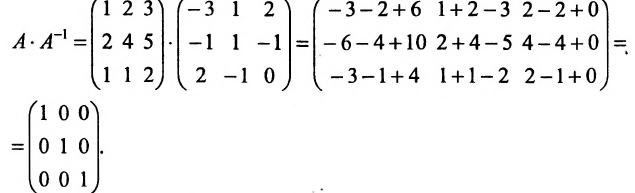
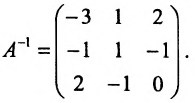
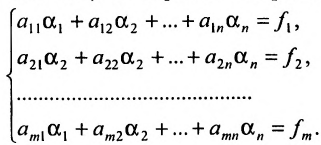
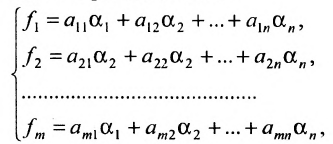
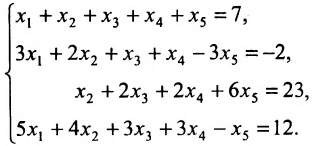

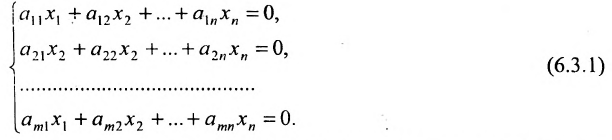
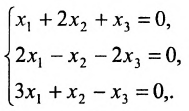
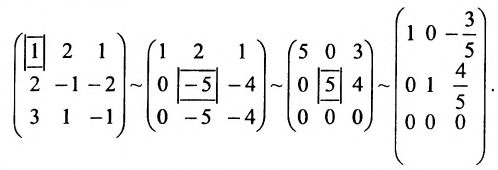
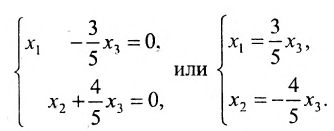
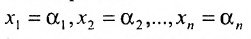
 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.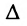 , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.