Составьте уравнение сферы если центр сферы

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

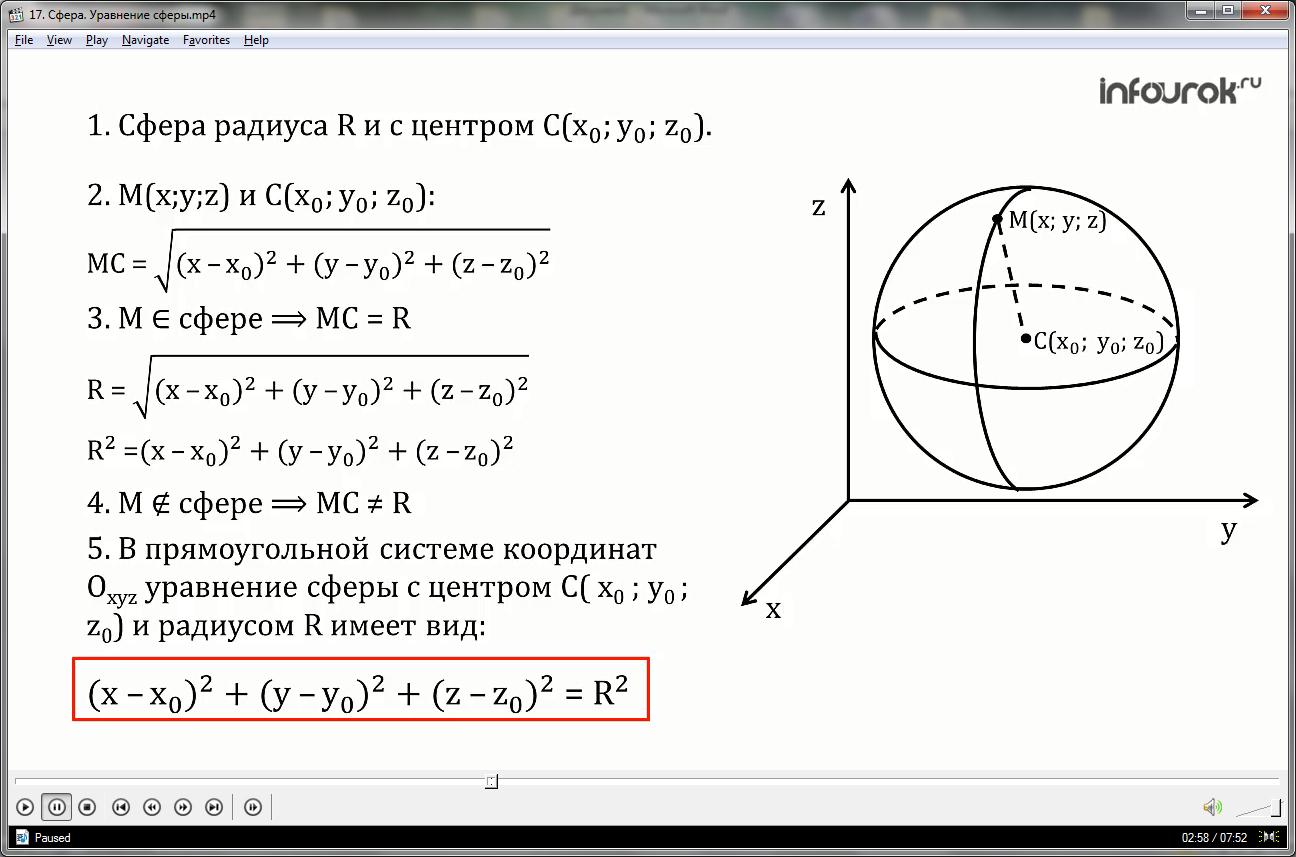
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

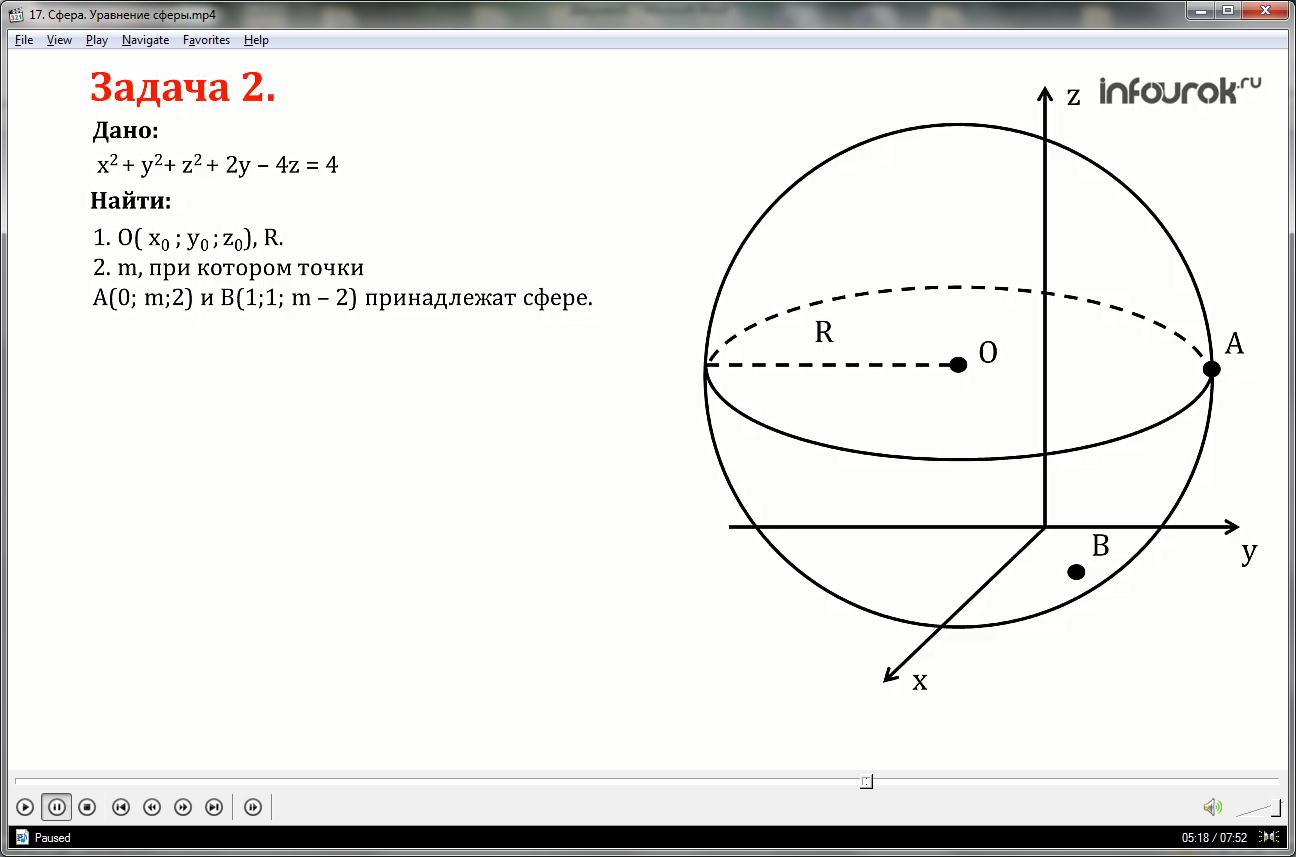
Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

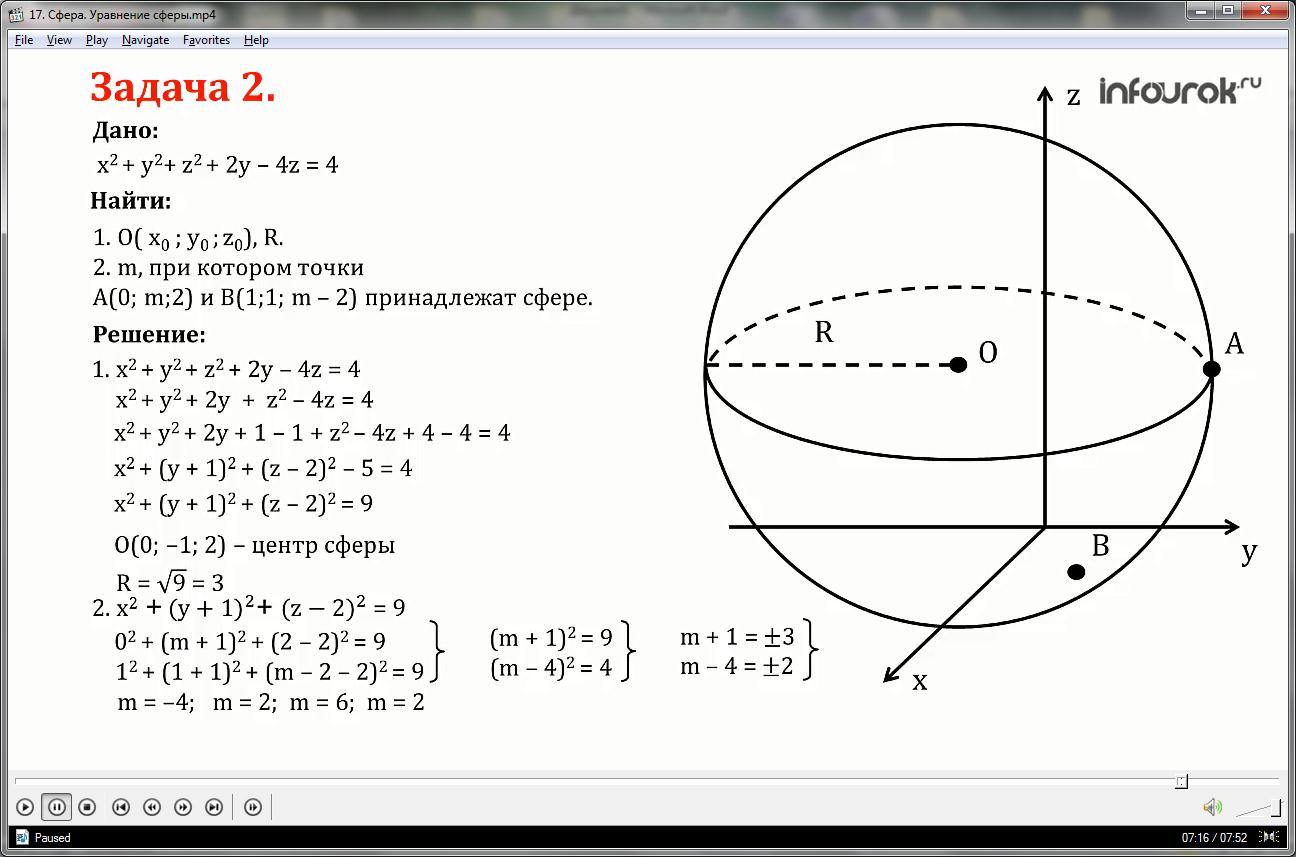
1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

51842

1003

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Составить уравнение сферы и найдите площадь её поверхности, если центром сферы является точка О (0 ; 1 ; — 2), а радиус 2 см?

Геометрия | 10 — 11 классы

Составить уравнение сферы и найдите площадь её поверхности, если центром сферы является точка О (0 ; 1 ; — 2), а радиус 2 см.

Уравнение сферы срадиусом r и центром в т.

(x — a)² + (y — b)² + (z — c)² = r²

(x — 0)² + (y — 1)² + (z — ( — 2))² = 2²

x² + (y — 1)² + (z + 2)² = 4

x² + y² — 2y + 1 + z² + 4z + 4 — 4 = 0

x² + y² + z² — 2y + 4z + 1 = 0.

Радиус сферы цилиндра 15см?

Радиус сферы цилиндра 15см.

Найди длину окружности сечения, удалённого от центра сферы на 12 см.

И площадь поверхности сферы.

Площадь сферы равна 1024 П см ^ 2?

Площадь сферы равна 1024 П см ^ 2.

Найдите радиус сферы.

На сфере радиусом 2 провели сечение радиусом 1 : а) на каком расстоянии от центра сферы проходит его плоскость ; б) какой угол фи составляет его плоскость с радиусом сферы, проведенным в точку сечения?

На сфере радиусом 2 провели сечение радиусом 1 : а) на каком расстоянии от центра сферы проходит его плоскость ; б) какой угол фи составляет его плоскость с радиусом сферы, проведенным в точку сечения?

Около конуса описана сфера?

Около конуса описана сфера.

Центр сферы совпадает с центром основания конуса.

Радиус сферы равен 51 корней из 2.

Найдите образующую конуса.

Вычислить площадь сферы и объём шара радиуса 2√5 см?

Вычислить площадь сферы и объём шара радиуса 2√5 см.

Составить уравнение сферы , если координаты центра равны ( — 5 ; две седьмых ; 1).

Через точку, лежащую на сфере, проведено сечение радиуса 3 см под углом 60 градусов к радиусу сферы, проведённому в данную точку?

Через точку, лежащую на сфере, проведено сечение радиуса 3 см под углом 60 градусов к радиусу сферы, проведённому в данную точку.

Найдите площадь сферы и объём шара.

СРОЧНО?

Точки А и B лежат на сфере.

Расстояние от центра сферы до прямой АВ равно 4 см.

Найдите радиус сферы, если АВ = 6 см.

ПОЖАЛУЙСТАА СРОЧНО НУЖЕН ОТВЕТ.

На расстояние 4 корня из 2 см?

На расстояние 4 корня из 2 см.

От центра сферы проведена секущая плоскости, радиус сферы проведённой в одну из точек линей пересечения составляет с плоскостью угол 45 градусов.

Найти площадь поверхности сферы.

«площадь поверхности сферы равна 324 п см?

«площадь поверхности сферы равна 324 п см.

Найти площадь другой сферы если ее радиус в 3 раза меньше радиуса данной сферы».

1)через точку на поверхности шара проведено в круг друзей под углом 60 к первой?

1)через точку на поверхности шара проведено в круг друзей под углом 60 к первой.

Найдите радиус шара если площадь сечения равна 12п см ^ 2.

2) Сфера радиуса R касаясь граней двугранного угла величина которого равна а.

Найдите расстояние от центра сферы до ребра двугранного угла.

3) Через точку на поверхности шара проведено две касательные прямые к шару.

Докажите что плоскость проходящая через эти прямые касательная к шару.

4) Периметр правельного триугольника равняется 72корень3 см, его стораны дотрангиваются к сфере.

Найдите расстаяние от центраа сферы к площади триугольника если вершины триугольника отдалена от центра сферы на 26 см.

Вы находитесь на странице вопроса Составить уравнение сферы и найдите площадь её поверхности, если центром сферы является точка О (0 ; 1 ; — 2), а радиус 2 см? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Составим уравнение по этой задаче : x / 5 + x = 180 6x / 5 = 180 6x = 180 * 5 6x = 900 x = 150 150 / 5 = 30 Ответ : 150 и 30.

2х = 60 — 60 2х = 0 х = 0 .

Угол BCD = 60 Угол DBC + BDC = 180 — 60 = 120 Угол DBC = 60 ABC = 180 — 60 = 129.

Угол BCD = 60 угол DBC + BDC = 180 — 60 = 120 угол DBC = 60 ABC = 180 — 60 = 120.

4 5 и 3 6 это накрест лежащие углы.

В середине 5 см а по бокам 17 так как 17 + 17 = 34 это отрезки по бокам и 34 + 5 = 39см Это отрезок AD.

Отрезок ТР — средняя линия треугольника АВС, она равна 2 см. Радиус окружности, вписанной в треугольник ВТР равен 1 / 3 ТN = 1 / 3 * ТР * sin P = 1 / 3 * 2 * √3 / 2 = √3 / 3. Угол MON равен 120, поэтому длина дуги MN равна 2π * √3 / 3 * 120 / 360 =..

Пусть одна сторона равна х, а другая х + 2, тогда 2х + 2(х + 2) = 44(периметр) 2х + 2х + 4 = 44 4х = 44 — 4 4х = 40 х = 40 : 4 х = 10 значит первая сторона = 10см 10 + 2 = 12 — вторая сторона площадь = х(х + 2) 10 * 12 = 120 см квадратных.

Вот так, я думаю, получается.

1) Нет 2) Да — в пространстве. Нет — на плоскости 3) Да — в пространстве. Нет — на плоскости 4) Да 5) Да 6) Да 7) Да 8) Нет 9) Нет (в общем случае радиусы могут лежать на одной прямой) 10) Да 11) Да 12) Да 13) Да 14) Да 15) Нет 16) Да 17) Да 18) Не..

Составьте уравнение сферы с радиусом, равным 3, если известно, что центр сферы лежит на оси Oz и сфера проходит через точку К(-2; -2; 1).

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,300
• гуманитарные 33,630
• юридические 17,900
• школьный раздел 607,261
• разное 16,836

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🔍 Видео