Даны уравнения двух сторон параллелограмма: 2Х + У + 3 = 0 и 2Х – 5У + 9 = 0 и уравнение одной из его диагоналей: 2Х – у — 3 = 0. Найти координаты вершин этого параллелограмма.
Выясните, уравнения каких сторон даны в условии задачи: параллельных или
Смежных, и как расположена данная диагональ по отношению к данным сторонам.
Выясним, уравнения каких сторон даны в условии задачи: параллельных или
Следовательно, прямые пересекаются, то есть даны уравнения смежных сторон параллелограмма.
Условие параллельности прямых

Пусть даны уравнения сторон АВ и AD. Тогда координаты точки А будут решением системы уравнений:
Теперь определим, уравнение какой диагонали: АС или BD – нам известно. Если это диагональ АС, то на ней лежит точка А, следовательно, координаты этой точки должны удовлетворять уравнению диагонали. Проверим:
Значит, точка А не лежит на данной прямой, то есть дано уравнение диагонали BD.
Тогда вершина В лежит на прямых АВ и BD, значит, ее координаты найдем из системы:
Система уравнений для определения координат точки D составлена из уравнений прямых AD И BD:
Остается найти координаты точки С. Составим уравнения прямых ВС и DC.
Поскольку ВС параллельна AD, их угловые коэффициенты равны. Найдем угловой коэффициент прямой AD:
Тогда ВС можно задать уравнением
Найдем координаты точки С, решив систему из двух полученных уравнений:
Найти точку, симметричную точке А(2; 1) относительно прямой, проходящей через точки В(-1; 7) и С(1; 8).
Представьте себе, что вам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
1) провести прямую ВС;
2) провести через точку А прямую, перпендикулярную ВС;
3) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.
Представим себе, что нам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
4) провести прямую ВС;
5) провести через точку А прямую, перпендикулярную ВС;
6) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.
Тогда точка А1 будет симметричной точке А относительно прямой ВС.
Теперь заменим каждое из действий составлением уравнений и вычислением координат точек.
1) Найдем уравнение прямой ВС в виде:
2) Найдем угловой коэффициент прямой ВС:
Прямая АО Перпендикулярна прямой ВС, поэтому
Составим уравнение прямой АО:
3) Найдем координаты точки О как решение системы:
4) Точка О – середина отрезка АА1, поэтому
Найти угол между прямыми L1: 3Х – у + 5 = 0 и L2: 2Х + У – 7 = 0.
Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда
Где K1 и K2 – угловые коэффициенты прямых L1 и L2.
Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда
Где K1 и K2 – угловые коэффициенты прямых L1 и L2. Найдем K1 и K2: для L1
Y = 3X + 5, K1 = 3; для второй: Y = -2X + 7, K2 = -2. Следовательно,
Для прямых А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0

Определить, лежит ли точка М(2; 3) внутри или вне треугольника, стороны которого заданы уравнениями 4Х – у – 7 = 0, Х + 3У – 31 = 0, Х + 5У – 7 = 0.
Если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне, а если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника.
Пусть первое уравнение задает сторону АВ, второе – ВС, третье – АС. Найдем координаты точек А, В и С:
Для ответа на вопрос задачи отметим, что:
1) если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне (т. е. точка М расположена относительно каждой стороны треугольника в одной полуплоскости с третьей вершиной);
2) если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника (на рисунке: точки М1 и В расположены по разные стороны от прямой АС).
Составим нормальные уравнения сторон треугольника АВС:
Вычислим соответствующие отклонения:
1) для точек М и А относительно прямой ВС:
2) для точек М и В относительно прямой АС:
3) для точек М и С относительно прямой АВ:
Итак, точки М И С лежат по разные стороны от прямой АВ. Следовательно, точка М расположена вне треугольника АВС.
Ответ: Точка М расположена вне треугольника АВС.
Для треугольника АВС с вершинами А(-3; -1), В(1; 5), С(7; 3) составить уравнения медианы и высоты, выходящих из вершины В.
Составьте уравнение медианы как прямой, проходящей через точки В и М – середину стороны АС, а высоты – как прямой, проходящей через точку В и перпендикулярной стороне АС.
1) Медиана ВМ проходит через точку В и точку М – середину отрезка АС. Найдем координаты точки М:
Тогда уравнение медианы можно записать в виде:
2) Высота ВН перпендикулярна стороне АС. Составим уравнение АС:
Ответ: медиана ВМ: 4Х + У – 9 = 0; высота ВН: 5Х + 2У – 15 = 0.
Определить, при каком значении А прямая
Параллельна оси ординат. Написать уравнение прямой.
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0
В = 0, С ≠ 0. Из условия В = 0 получаем: А2 – 1 = 0, А = ± 1.
При А = 1 С = 2 + 7 – 9 = 0 – второе условие не выполняется (получившаяся при этом прямая -4Х = 0 не параллельна оси Оу, а совпадает с ней).
При А = -1 получим: -6Х – 14 = 0, 3Х + 7 = 0.
Составить уравнения всех прямых, проходящих через точку М(2; 3) и отсекающих от координатного угла треугольник площадью 12.
Составьте уравнение искомой прямой «в отрезках»:
Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда
Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках».
Составим уравнение искомой прямой «в отрезках»:
Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда
Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках». Таким образом, для А и B можно составить систему уравнений:
Следовательно, условию задачи удовлетворяют три прямые:
- Задача 59148 Подскажите как правильно решать! Найти.
- Условие
- Решение
- Точки A( — 2 ; 4), B( — 6 ; 12)и C(2 ; 8) являются вершинами параллелограмма ABCD?
- Точки A( — 1?
- Точки А(2 ; 3 ; — 5), С(3 ; 6 ; 8) и D(5 ; 4 ; — 1) являются вершинами параллелограмма ABCD?
- Точки В ( — 4 ; 2) и D(2 ; — 4) являются противоположными вершинам квадрата ABCD?
- СРОЧНО?
- Даны три вершины параллелограмма ABCD : B( — 1 ; 1), C(2 ; 3), D(1 ; — 1)?
- EK — диагональ параллелограмма EFKD , Е( — 4 ; 3), К( 2 ; 5)?
- Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая сторону AB в точке M, а сторону CD в точке N?
- В параллелограмме ABCD диагонали пересекаются в точке E?
- Дано три вершины параллелограмма АВСД : В ( — 1 ; 7), С (7 ; 3), Д (5 ; — 1) 1)Найдите координаты точки К пересечения диагоналей и координаты четвертой вершины параллелограмма?
- В параллелограмме PQRS известны координаты точки пересечения диагоналей A( — 2 ; 1) и двух вершин Q(2 ; 4) и R(1 ; — 3)?
- 💥 Видео
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Задача 59148 Подскажите как правильно решать! Найти.
Условие
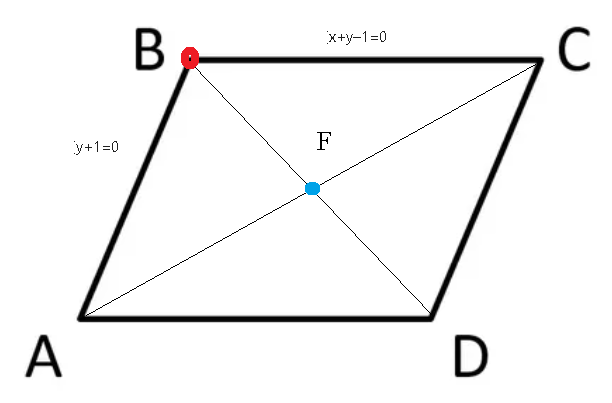
Подскажите как правильно решать! Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x+y-1=0 если у+1=0 если известно что диагональ параллелограмма пересекается в точке F(-1, 0) И надо ли в этой задаче чертить рисунок?
Решение
Можно нарисовать схематический чертеж, чтобы понять как решать задачу ( cм. рис)
Противоположные стороны параллелограмма параллельны.
Даны уравнения смежных сторон. Это может быть АВ и ВС
1) чтобы найти точку пересечения сторон АВ и ВС
Это и есть координаты точки B.
2)
Составить уравнение прямой, проходящей через две точки:
(2;-1) и F(–1, 0)
Это можно сделать двумя способами:
Уравнение прямой с угловым коэффициентом имеет вид:
y=kx+b
Подставляем координаты точек:
-1=k*2+b
0=k*(-1)+b
находим k и b
[b]x+3y+1=0[/b] — это ответ.
Второй способ
Уравнение прямой, проходящей через две точки имеет вид: ( cм. скрин)
Подставляем координаты точек
и получаем пропорцию:
[b]x+3y+1=0[/b]- ответ. 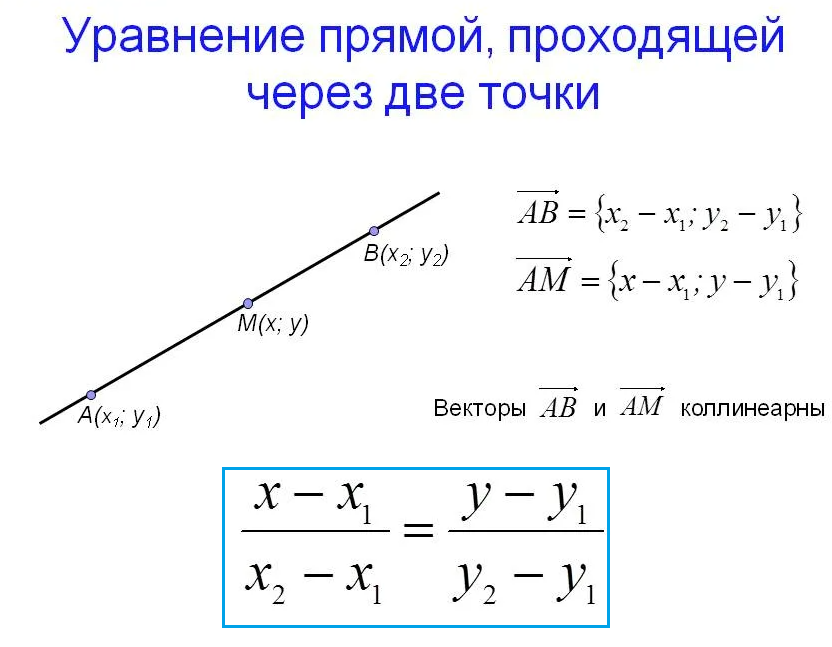
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Точки A( — 2 ; 4), B( — 6 ; 12)и C(2 ; 8) являются вершинами параллелограмма ABCD?
Математика | 5 — 9 классы
Точки A( — 2 ; 4), B( — 6 ; 12)и C(2 ; 8) являются вершинами параллелограмма ABCD.
Найдите : а) координаты точки пересечения диагоналей ; б) длины сторон параллелограмма ; в) координаты его четвёртой вершины.
2. Запишите уравнение прямых , на которых лежат диагонали параллелограмма ABCD из задания 1.
Должны получится ответы : 1.
4 кв корень из 5 , в (6 ; 0) .
2. y + x — 6 = 0, y — x — 6 = 0.
А)в параллелограмме диагонали в точке пересечения делятся пополам, возьмем диагональ АС, найдем координаты середины
х = — 2 + 2 / 2 = 0 у = 4 + 8 / 2 = 6 О(0 ; 6)
б) АВ = √ ( — 6 + 2)2 + (12 — 4)2 = √16 + 64 = √80 = 4√5
ВС = √(2 + 6)2 + (8 — 12)2 = √64 + 16 = √80 = 4√5
в) середина диагонали ВД точка О(0 ; 6) х2 = 2 * 0 — ( — 6) = 6 у2 = 2 * 6 — 12 = 0 точка Д(6 ; 0)
г) диагонали АС А( — 2 : 4) С(2 : 8)
формула прямой : (х — х1)(у2 — у1) = (у — у1)(х2 — х1)
АС : (х + 2)(8 — 4) = (у — 4)(2 + 2) 4х + 8 = 4у — 16 4х — 4у + 24 = 0 разделим все на ( — 4) получим у — х — 6 = 0
ВД : B( — 6 ; 12)Д(6 ; 0) (х + 6)(0 — 12) = (у — 12)(6 + 6) — 12х — 72 = 12у — 144 — 12х — 12у + 72 = 0 разделим все на ( — 12) у + х — 6 = 0,.
Видео:№980. Напишите уравнения прямых, содержащих стороны ромба, диагонали которого равны 10 см и 4 см,Скачать

Точки A( — 1?
— 2) являются вершинами параллелограмма .
Найдите сумму координат четвертой вершины этого параллелограмма.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Точки А(2 ; 3 ; — 5), С(3 ; 6 ; 8) и D(5 ; 4 ; — 1) являются вершинами параллелограмма ABCD?
Точки А(2 ; 3 ; — 5), С(3 ; 6 ; 8) и D(5 ; 4 ; — 1) являются вершинами параллелограмма ABCD.
Найдите длину диагонали BD.
Видео:Видеоурок "Канонические уравнения прямой"Скачать

Точки В ( — 4 ; 2) и D(2 ; — 4) являются противоположными вершинам квадрата ABCD?
Точки В ( — 4 ; 2) и D(2 ; — 4) являются противоположными вершинам квадрата ABCD.
Найдите координаты остальных вершин и координаты точки, которая делить сторону ADпополам ?
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

СРОЧНО?
В параллелограмме ABCD известны координаты точки пересечения диагоналей Е (1 ; — 2) и двух верршин А ( — 4 ; — 3) и В ( — 2 ; 5).
Найдите координаты двух других вершин параллелограмма.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Даны три вершины параллелограмма ABCD : B( — 1 ; 1), C(2 ; 3), D(1 ; — 1)?
Даны три вершины параллелограмма ABCD : B( — 1 ; 1), C(2 ; 3), D(1 ; — 1).
Найдите координаты вершины A и длину стороны AD.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

EK — диагональ параллелограмма EFKD , Е( — 4 ; 3), К( 2 ; 5)?
EK — диагональ параллелограмма EFKD , Е( — 4 ; 3), К( 2 ; 5).
Найдите координаты точки пересечения диагоналей параллелограмма.
Видео:Уравнения стороны треугольника и медианыСкачать

Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая сторону AB в точке M, а сторону CD в точке N?
Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая сторону AB в точке M, а сторону CD в точке N.
Найдите площадь параллелограмма ABCD, если площадь четырёхугольника AMND равна 48м в квадрате.
Видео:17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

В параллелограмме ABCD диагонали пересекаются в точке E?
В параллелограмме ABCD диагонали пересекаются в точке E.
Найдите диагонали параллелограмма, если AE = 3ли, BE = 5дм.
Видео:8 класс, 4 урок, ПараллелограммСкачать

Дано три вершины параллелограмма АВСД : В ( — 1 ; 7), С (7 ; 3), Д (5 ; — 1) 1)Найдите координаты точки К пересечения диагоналей и координаты четвертой вершины параллелограмма?
Дано три вершины параллелограмма АВСД : В ( — 1 ; 7), С (7 ; 3), Д (5 ; — 1) 1)Найдите координаты точки К пересечения диагоналей и координаты четвертой вершины параллелограмма.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В параллелограмме PQRS известны координаты точки пересечения диагоналей A( — 2 ; 1) и двух вершин Q(2 ; 4) и R(1 ; — 3)?
В параллелограмме PQRS известны координаты точки пересечения диагоналей A( — 2 ; 1) и двух вершин Q(2 ; 4) и R(1 ; — 3).
Найдите координаты двух других вершин параллелограмма.
ПОМОГИТЕ СРОЧНО, ПОЖАЛУЙСТА!
На странице вопроса Точки A( — 2 ; 4), B( — 6 ; 12)и C(2 ; 8) являются вершинами параллелограмма ABCD? из категории Математика вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.
1)327 — 20 * x = 267 — 20x = 267 — 327 — 20x = — 60 x = — 60 : ( — 20) x = 60 : 20 x = 30 2)48 * x + 568 = 1000 48x = 1000 — 568 48x = 432 x = 432 : 48 x = 9 3)425 : x + 432 = 437 425 : x = 437 — 432 425 : x = 5 x = 425 : 5 x = 85.
327 — 20•x = 267 20 * x = 327 — 267 20 * x = 60 x = 60 : 20 x = 3 48•x + 568 = 1000 48 * x = 1000 — 568 48x = 432 x = 432 : 48 x = 9 425 : x + 432 = 437 425 : x = 437 — 432 425 : x = 5 x = 425 : 5 x = 85.
А) 7×4 = 28 б) 3×7 = 21 в) 12×3 = 36.
Если пять дней в неделю : 1. 70х5 = 350 — первая неделя 2. 80х5 = 400 — вторая неделя 3. 350 + 400 = 750 — итого Ответ : 750 Если шесть дней в неделю : 1. 70х6 = 420 — первая неделя 2. 80х6 = 480 — вторая неделя 3. 420 + 480 = 900 — итого Ответ..
28 двадцать восемь 60 шестьдесят 90 девяносто 100 сто 40 сорок.
2 дес 8 ед = 28 6 дес = 60 9 дес = 90 10 дес = 100 4 дес = 40.
НАИБОЛЬШОЕ 5 ЗНАЧНОЕ ЧИСЛО САСТАВЛЕНО И ЦЫФР 1 2 3 НАИБОЛЬШОЕ ЧИСЛО 33321 НАИМЕНЬШЕЕ 11123 ВЫЧЕТАЕМ ОДНО ИЗ ДРУГОГО 33321 — 11123 = 22198.
Наибольшее число : 33333 Наименьшее число : 11111 33333 — 11111 = 22222 Ответ : 2).
1)45 : 250 * 100% = 18% 2)18 / 50 * 100% = 36%.
Вместо / пиши дробь. 2 / 6 = 1 / 3 6 / 14 = 3 / 7 6 / 9 = 2 / 3 5 / 15 = 1 / 3 3 / 9 = 1 / 3 10 / 22 = 5 / 11 12 / 15 = 4 / 5 10 / 35 = 2 / 7 4 / 12 = 1 / 3 12 / 14 = 6 / 7 18 / 21 = 6 / 7 6 / 18 = 1 / 6 5 / 25 = 1 / 5 18 / 28 = 9 / 14 30 / 33 = 10 ..
💥 Видео
9 класс, 7 урок, Уравнение прямойСкачать

Математика это не ИсламСкачать

найти уравнения биссектрис углов между прямымиСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Как составить уравнение прямой, проходящей через две точки. Урок 3. Геометрия 8 класс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать