Составьте уравнение плоскости проходящей через точку а и перпендикулярной прямой ав если

Условие

уравнение плоскости, проходящей через точку А и перпендикулярной прямой АВ, если А(-1,2,1), В(-3,1,-2)

Решение

Составляем уравнение прямой АВ как прямой, проходящей через две точки.

Направляющий вектор этой прямой (-2;-1;-3) является нормальным вектором плоскости.

Составляем уравнение плоскости, проходящей через точку и имеющей нормальный вектор.

-2*(х — (-1)) — 1*(y — 2) — 3*(z -1)=0

Раскрываем скобки и получаем ответ

—

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ. ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.38 Задача 65

Кто поможет с решением? Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ, если:
1) А(-1; 1; 2), В(2; 0; 1);
2) А( 1; 0; -1), В(4; 6; -3);
3) А(3; -4; 5), В(2; 1; -3).

Лови уравнения.
1) п = АВ = (3; -1; -1)
Уравнение искомой плоскости: 3(х — (—1)) + (— 1 )(у — 1) + (-1)
(z — 2) = 0; 3х -у — z + 6 = 0
2) п = АВ = (3; 6; -2)
Уравнение искомой плоскости: 3(х — 1) +
+ 6(у — 0) + (-а )(z-(-l)) = 0; 3x + 6y-2z-5 =0.
3) п=AB = (-1; 5; -8)
Уравнение искомой плоскости: (-1)(x — 3) + 5(у — (- 4)) +
+ (- 8)(z — 5) = 0; — х + 5у — 8z + 63 = 0; х — 5у + 8z — 63 = 0

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения

.

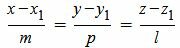(1)

Построить уравнение плоскости α, проходящей через точку M₀ и перпендинулярной прямой L.

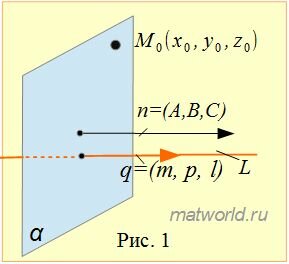Решение. Уравнение плоскости, проходящей через точку M₀ и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:

Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:

Упростим уравнение (3):

Таким образом уравнение (4) определяет плоскость, проходящей через точку M₀(x₀, y₀, z₀) и перпендикулярной прямой (1).

Ответ. Уравнение плоскости прпоходящей через точку M₀(x₀, y₀, z₀) и перпендикулярной прямой (1) имеет вид (4).

Пример 1. Найти уравнение плоскости α, проходящую через точку M₀(3, −1, 2) и перпендикулярной прямой L:

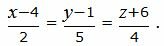(7)

Решение. Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).

Направляющий вектор прямой L имеет следующий вид: :

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:

Подставляя координаты точки M₀ и направляющего вектора q в (8), получим:

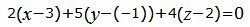(9)

Упростим уравнение (9):

Ответ: Уравнение плоскости, проходящей через точку M₀(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).

Пример 2. Найти уравнение плоскости α, проходящую через точку M₀(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:

(11)

Решение. Приведем параметрическое уравнение (11) к каноническому виду:

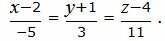(11′)

Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n=<A, B, C> представляется формулой:

Направляющий вектор прямой L имеет следующий вид:

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:

Подставляя координаты точки M₀ и направляющего вектора q в (13), получим:

Упростим уравнение (13):

Ответ. Уравнение плоскости, проходящей через точку M₀(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).

Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ, если А ( — 1, 1, 2) и В (2, 0, 1)?

Геометрия | 10 — 11 классы

Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ, если А ( — 1, 1, 2) и В (2, 0, 1).

Y = x2 + 4x — 2 вот тебе уравнение плоскости которая проходит через точку А и перпендикулярна прямой АВ.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

В кубе АВСДА1В1С1Д1 укажите плоскости, перпендикулярные прямой АВ?

В кубе АВСДА1В1С1Д1 укажите плоскости, перпендикулярные прямой АВ.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Отрезок АВ не пересекает плоскость L?

Отрезок АВ не пересекает плоскость L.

Через точки А и В проведены прямые, перпендикулярные плоскости L и пересекающие ее в точках А и В.

Найти А1В1, если АВ = 13см.

АА1 = 3см, ВВ1 = 8см.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Через точку А, удаленную от плоскости альфа на 3 см, проходит пряма, пересекающая плоскость альфа в точке В?

Через точку А, удаленную от плоскости альфа на 3 см, проходит пряма, пересекающая плоскость альфа в точке В.

Угол между прямой АВ и плоскостью альфа равен arcsin0, 6.

Найдите длину отрезка АВ.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Решить за дачу : Отрезок АВ лежит в одной из двух перпендикулярных плоскостей и не пересекает другую?

Решить за дачу : Отрезок АВ лежит в одной из двух перпендикулярных плоскостей и не пересекает другую.

Точки А и В удалены от прямой с пересечения плоскостей на 18см и 10 см соответственно.

Во второй плоскости параллельно прямой с провели прямую b, от которой точка А удалена на 30см.

Найдите расстояние от точки В до этой прямой.

Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Прямая AM перпендикулярна к плоскости квадрата ABCD, диагонали которого пересекаются в точке O?

Прямая AM перпендикулярна к плоскости квадрата ABCD, диагонали которого пересекаются в точке O.

Докажите что прямая BD перпендикулярна к плоскости AMO.

MO перпендикулярна BD.

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Прямая АМ перпендикулярна плоскости квадрата АВСД, диагонали которого пересекаются в точке О?

Прямая АМ перпендикулярна плоскости квадрата АВСД, диагонали которого пересекаются в точке О.

Докажите, что прямая ВD перпендикулярна плоскости АМО.

Видео:3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Даны точки А( — 2 ; 0) и В(4 ; 6)?

Даны точки А( — 2 ; 0) и В(4 ; 6).

А)Найдите расстояние между точками А и В.

Б) Запишите уравнение прямой , АВ.

В) Составьте уравнение прямой , которая проходит черезсердину АВ и параллельна прямой у = 2х = 5.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Через точку А удалённую от плоскости на 3см проходит прямая пересекающая плоскость альфа в точке В?

Через точку А удалённую от плоскости на 3см проходит прямая пересекающая плоскость альфа в точке В.

Угол между прямой АВ и плоскостью равен 30°.

Найдите длину отрезка АВ.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Прямая АВ касается окружности основания цилиндра в точке А?

Прямая АВ касается окружности основания цилиндра в точке А.

Доказать, что прямая АВ перпендикулярна до плоскости АОО₁A₁.

Видео:17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Даны взаимно перпендикулярные и прямая а плоскость Сколько прямых можно провести так, из данной точки плоскости a так, чтобы они были перпендикулярны прямой а и лежали в плоскости а ?

Даны взаимно перпендикулярные и прямая а плоскость Сколько прямых можно провести так, из данной точки плоскости a так, чтобы они были перпендикулярны прямой а и лежали в плоскости а ?

Если вам необходимо получить ответ на вопрос Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ, если А ( — 1, 1, 2) и В (2, 0, 1)?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

360 — 240 = 120. — один угол. Второй тоже 120 потом 360 — (120 + 120) = 120 — два угла 120 ÷2 = 60 — два угла Ответ : 60 , 120 , 120, 60.

Оно имеет границу, непосредственно если не было границ не было и фигур.

Ответ 75. 180 — 90 — 15 = 75. Сумма углов треугольника = 180.

Т. к противоположные стороны паралелограмма равны, то .

При пересечении двух прямых образуется 4 угла. Вертикальные углы равны L1 = L3 L2 = L4 Сумма 4 углов = 360° L4 = 360° — 226° = 134° = L2 L1 + L3 = 226° — L2 = 226° — 134° = 92° L1 = L3 = 92° : 2 = 46° Ответ : два угла по 46° и два по 134°.

Площади подобных треугольников относятся как коэффициент пропорциональности в квадрате k² 6 / 24 = k² k² = ¼ k = ½ Ответ : ½.

Пусть равные стороны равны х, в основание 3х. Тогда получается х + х + 3х = 25 5х = 35 х = 7 Основание = 21 Ответ : 7, 7, 21.

ОАD = 90° — 55° = 35°. AO = OD т. К. это прямоугольник, значит ОАD = ОDА = 35°. АОD = 180° — ОАD — ODА = 180° — 35° — 35° = 110° (сумма углов в треугольнике равна 180°) Ответ : АОD = 110°.

🌟 Видео

Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

Уравнение плоскости через точку и нормальСкачать

Уравнение плоскости через 3 точкиСкачать

Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать

Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать