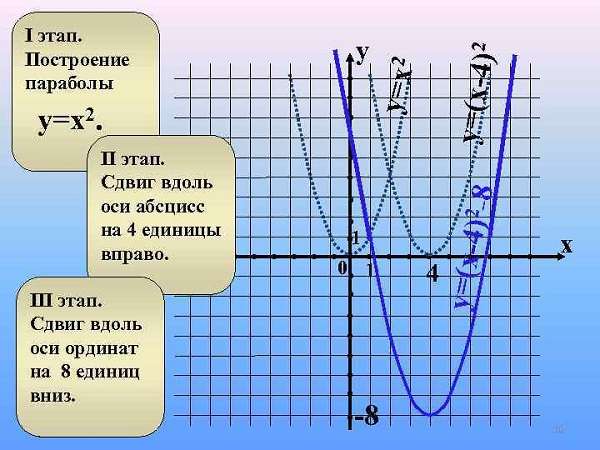
Математика | 10 — 11 классы
Уравнение оси параболы.
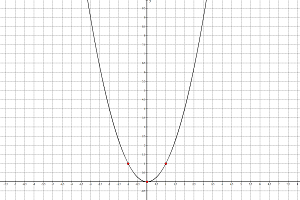
Дана парабола Составьте уравнение её оси.
Запишем уравнение в другом виде :
$20y=- x^2- 6x+ 51 \ y=-0,05x^2-0,3x+2,55$
Уравнение оси имеет вид : $x=- frac$
Подставим коэффициенты из нашего уравнения :
- Запишите уравнение оси симметрии параболы у = — 4(х — 2) ^ 2?
- 1. Парабола задана уравнение y = x в квадрате — 4x — 5?
- Записать уравнение параболы, полученной на параболы y = — 3x в квадрате : 1)сдвигом вдоль оси Oy на 1 единицу вверх 2)Сдвигом вдоль оси Oy на 5 единиц вниз объясните пожалуйста?
- Запишите уравнение параболы, если она получена сдвигом параболы y = — 7x ^ 2 вдоль осей координат и её вершина находится в точке (10 ; 4)?
- Вычислить объём тела образованного вращением вокруг оси Ох фигуры ограниченной параболой , прямой и осью Ох?
- Какой угол образует с осью абсцисс касательная к параболе у = х2 — Зх + 5, проведенная в точке М(2 ; 3)?
- Найдите сумму тангенсов углов наклона касательных к параболе y = x ^ 2 — 9 в точках пересечения параболы с осью абсцисс?
- Напишите уравнения оси симметрии параболы y = x ^ 2 + 4x — 5?
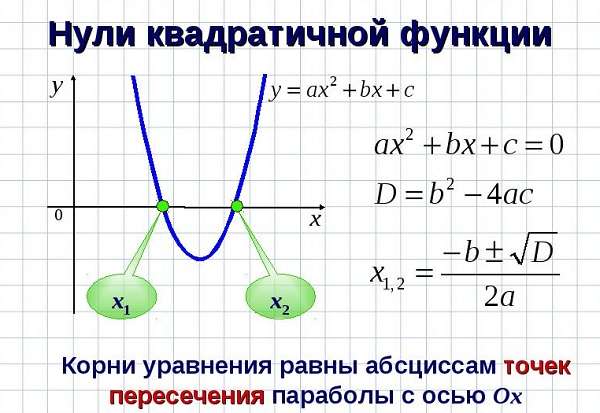
- Сколько точек пересечения у параболы и ос абсцисс Напишите подробно и понятно, пожалуйста?
- Если дискриминант положителен, то сколько будет пересечений оси с параболой?
- Парабола свойства и график квадратичной функции
- Что такое парабола и как она выглядит
- Каноническое уравнение параболы
- Свойства и график квадратичной функции
- Как определить, куда направлены ветви параболы
- Как найти вершину параболы по формуле
- Смещение параболы
- Как строить параболу по квадратному уравнению
- Директриса, эксцентриситет, фокус параболы
- Заключение
- Запишите уравнение оси симметрии параболы: а) у = (х — 12)2; б) у = -(х + 7)2; в) у = 3(х + 2)2; г) у = -8(х — 10)2.
- Ваш ответ
- решение вопроса
- Похожие вопросы
Видео:Вершина параболы и ось симметрии. ПримерСкачать

Запишите уравнение оси симметрии параболы у = — 4(х — 2) ^ 2?
Запишите уравнение оси симметрии параболы у = — 4(х — 2) ^ 2.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

1. Парабола задана уравнение y = x в квадрате — 4x — 5?
1. Парабола задана уравнение y = x в квадрате — 4x — 5.
А) Найдите координаты вершины параболы.
Б) Определите , куда (вверх или вниз) направлены ветви параболы , и объясните почему.
В) Постройте параболу.
Г) Найдите координаты точек пересечения параболы с осью абцисс.
2. Найдите наименьшее значение функции y = x в квадрате — 4x — 5.
Видео:Вариант 72, № 5. Уравнение оси симметрии параболы. Пример 2Скачать

Записать уравнение параболы, полученной на параболы y = — 3x в квадрате : 1)сдвигом вдоль оси Oy на 1 единицу вверх 2)Сдвигом вдоль оси Oy на 5 единиц вниз объясните пожалуйста?
Записать уравнение параболы, полученной на параболы y = — 3x в квадрате : 1)сдвигом вдоль оси Oy на 1 единицу вверх 2)Сдвигом вдоль оси Oy на 5 единиц вниз объясните пожалуйста.
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Запишите уравнение параболы, если она получена сдвигом параболы y = — 7x ^ 2 вдоль осей координат и её вершина находится в точке (10 ; 4)?
Запишите уравнение параболы, если она получена сдвигом параболы y = — 7x ^ 2 вдоль осей координат и её вершина находится в точке (10 ; 4).
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Вычислить объём тела образованного вращением вокруг оси Ох фигуры ограниченной параболой , прямой и осью Ох?
Вычислить объём тела образованного вращением вокруг оси Ох фигуры ограниченной параболой , прямой и осью Ох.
Видео:Как построить график функции без таблицыСкачать

Какой угол образует с осью абсцисс касательная к параболе у = х2 — Зх + 5, проведенная в точке М(2 ; 3)?
Какой угол образует с осью абсцисс касательная к параболе у = х2 — Зх + 5, проведенная в точке М(2 ; 3)?
Написать уравнение этой касательной.
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Найдите сумму тангенсов углов наклона касательных к параболе y = x ^ 2 — 9 в точках пересечения параболы с осью абсцисс?
Найдите сумму тангенсов углов наклона касательных к параболе y = x ^ 2 — 9 в точках пересечения параболы с осью абсцисс.
Видео:Как легко составить уравнение параболы из графикаСкачать

Напишите уравнения оси симметрии параболы y = x ^ 2 + 4x — 5?
Напишите уравнения оси симметрии параболы y = x ^ 2 + 4x — 5.
Видео:Как определить уравнение параболы по графику?Скачать

Сколько точек пересечения у параболы и ос абсцисс Напишите подробно и понятно, пожалуйста?
Сколько точек пересечения у параболы и ос абсцисс Напишите подробно и понятно, пожалуйста.
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Если дискриминант положителен, то сколько будет пересечений оси с параболой?
Если дискриминант положителен, то сколько будет пересечений оси с параболой?
Вы зашли на страницу вопроса Уравнение оси параболы?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.
Для нахождения пределов необходимо подставить число, к которому стремится переменная, в выражение под знаком предела, и, если нет неопределённостей, вычислить его : 1) lim(3³ + 3 — 5) = 25 ; 2) lim(2 * ( — 3) / 1) = — 6.
7т — 6т 500 кг = 0, 5т. 9т277кг — 9т109 = 0, 72. 8т500кг — 7т700кг = 0. 8 4т230кг — 3т600кг = 0. 63т.
Да, между 3 — мя людьми нет ничего общего, но 4 — й может иметь общее с каким нибудь человеком из этих трёх.
Ответ : Нет, так как из трёх людей 2 обязательно будут с одинаковым именем, фамилией или отчеством. Я такое задание в олимпиаде делала)).
50. 505 — 45. 556 = 4. 949 768 : 6 = 128.
50. 505 — 45. 556 = 4. 949 768 : 6 = 128.
Нет. сумма сумм всех столбцов равна сумме сумм всех строк равна сумме всех чисел. Но сумма 5 отрицательных чисел не равна сумме 5 положительных.
Вот такааааая 504116.
504116 — эта последовательность цифр.
31200 + х = 75883 — 999 31200 + х = 75784 х = 75784 — 31200 х = 44584 5376 — а = 3887 + 904 5376 — а = 4791 А = 5376 — 4791 А = 585 Надеюсь вы поняли как решать остальные. Если нет , то по буквам могу решить , просто долго писать цифры.
Видео:КАК СТРОИТЬ ПАРАБОЛУ. ОСЬ СИММЕТРИИ (Финальная часть саги о функциях)Скачать

Парабола свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
- Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
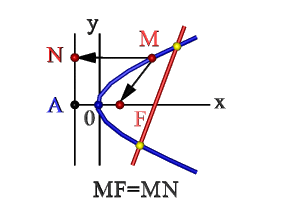
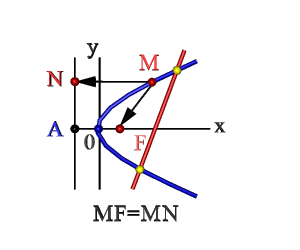
- Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.
Видео:График функции y=x² (y=аx).Скачать

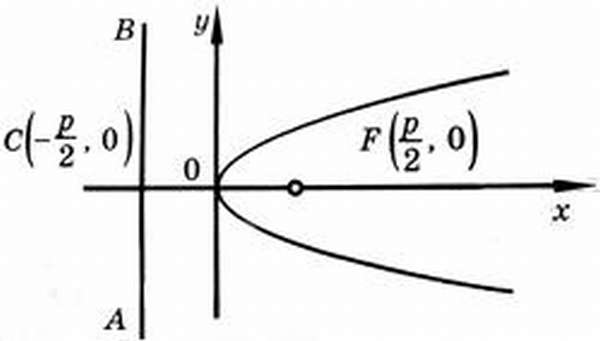
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Видео:Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
Видео:Квадратичная функция и ее график. 8 класс.Скачать

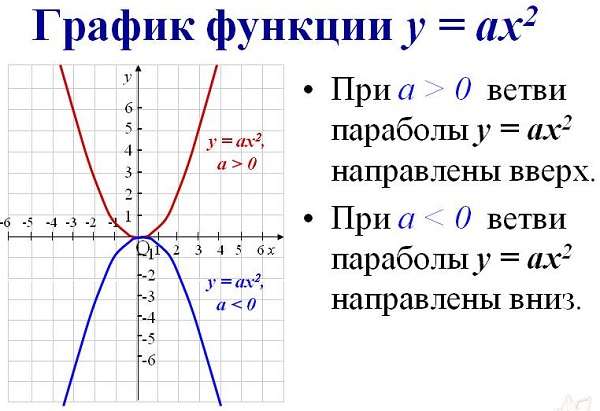
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Видео:Построить график функции y=x2. Парабола.Скачать
Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Для такой линии:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Видео:Парабола. Квадратичная функцияСкачать

Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
- Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
- D = 0, то х1, 2 = -b / (2 * a),
- D ˂ 0, то нет точек пересечения с вектором ОХ.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью ординат,
- найти пересечение с осью абсцисс.
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
- а = 1, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
- с осью ординат пересекается в значении у = 4,
- найдем дискриминант: D = 25 — 16 = 9,
- ищем корни:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5 — 3) / 2 = 1, (1, 0).
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
- а = 3, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
- с осью у будет пересекаться в значении у = -1,
- найдем дискриминант: D = 4 + 12 = 16. Значит корни:
- Х1 = (2 + 4) / 6 = 1, (1,0),
- Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).
По полученным точкам можно построить параболу.
Видео:Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

Директриса, эксцентриситет, фокус параболы
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.
Эксцентриситет (константа) = 1.
Видео:Как строить параболу? | TutorOnlineСкачать

Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
Запишите уравнение оси симметрии параболы: а) у = (х — 12)2; б) у = -(х + 7)2; в) у = 3(х + 2)2; г) у = -8(х — 10)2.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,427
- гуманитарные 33,634
- юридические 17,906
- школьный раздел 608,218
- разное 16,858
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.