Составьте уравнение касательной к графику функции y x8 4×4 5

Алгебра | 10 — 11 классы

Составьте уравнение касательных к графику функции y = x ^ 8 + 4x ^ 4 — 5 в точках его пересечения с осью абсцисс.

Найдите точку пересечения этих касательных.

Сначала найдём точки пересечения с осью абсцисc : x ^ 8 + 4x ^ 4 — 5 = 0 ; t = x ^ 4 ; t ^ 2 + 4t — 5 = 0 ; D = 36 ; t1 = — 5 (посторонний корень, т.

К. чётная степень не может быть отрицательной) ; t2 = 1 ; x ^ 4 = 1 ; x1 = — 1 ; x2 = 1.

Найдём уравнения касательных в этих точках.

Y’ = 8x ^ 7 + 16x ^ 3 ; y’(1) = 24 ; y’( — 1) = — 24 , касательная в точке х = 1 : y = 24x — 24 ; касательная в точке х = — 1 : y = — 24x — 24 ; найдём точку пересечения : 24x — 24 = — 24x — 24 ; x = 0 ; y(0) = — 5 ; M(0, — 5) — ответ.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Вычислите площадь фигуры ограниченной графиком функции y = — 1 / 4 x ^ 2 + 1 и касательными проведенными к этому графику в точках его пересечения с осью абсцисса?

Вычислите площадь фигуры ограниченной графиком функции y = — 1 / 4 x ^ 2 + 1 и касательными проведенными к этому графику в точках его пересечения с осью абсцисса.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Составьте уравнение касательной проведенной к графику функции y = е ^ x / 2 через его точку пересечения с осью ординат СРОЧНООООО?

Составьте уравнение касательной проведенной к графику функции y = е ^ x / 2 через его точку пересечения с осью ординат СРОЧНООООО!

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Напишите уравнение касательной к графику функции f(x) = ln(8x + 9) — ln(2x + 3) в точке пересечения этого графика с осью абсцисс?

Напишите уравнение касательной к графику функции f(x) = ln(8x + 9) — ln(2x + 3) в точке пересечения этого графика с осью абсцисс.

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Составьте уравнение касательной к графику функции y = x ^ 4 — 2x ^ 2 — 8 в точках его пересечения с осью абцисс?

Составьте уравнение касательной к графику функции y = x ^ 4 — 2x ^ 2 — 8 в точках его пересечения с осью абцисс.

Найдите точьку пкресечения этих касательных.

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Найдите тангенс угла наклона касательной к графику функции F(x) = x3 — 27 в точке пересечения этого графика с осью абсцисс?

Найдите тангенс угла наклона касательной к графику функции F(x) = x3 — 27 в точке пересечения этого графика с осью абсцисс.

Видео:Производная: касательная к графику.Скачать

К графику функции f(x) = — x ^ 2 — 5x проведена касательная в точке Р ( — 1 : 4)?

К графику функции f(x) = — x ^ 2 — 5x проведена касательная в точке Р ( — 1 : 4).

Найдите абсциссу точки пересечения касательной с осью ОХ.

Видео:Уравнение касательнойСкачать

Написать уравнение касательной к графику функции y = 8×3 — 1 в точке пересечения его с осью абсцисс?

Написать уравнение касательной к графику функции y = 8×3 — 1 в точке пересечения его с осью абсцисс.

Видео:Уравнение касательнойСкачать

Составьте уравнение касательных к графику функции х ^ 4 + x ^ 2 — 2 , в точках его пересечения с осью абсцисс ?

Составьте уравнение касательных к графику функции х ^ 4 + x ^ 2 — 2 , в точках его пересечения с осью абсцисс .

Найти точку пересечения этих касательных .

Пожалуйста последний пункт подробно.

Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Касательная проведена к графику функции f(x) = ( x + 1 ) в 3 степени + 3x + 3 в точке его пересечения с осью абсцисс?

Касательная проведена к графику функции f(x) = ( x + 1 ) в 3 степени + 3x + 3 в точке его пересечения с осью абсцисс.

Найдите координаты точки пересечения этой касательной с прямой y = 12.

Видео:Геометрический смысл производной. Уравнение касательнойСкачать

Составьте уравнение касательной к графику функции f(x) = e ^ x / 3, проведённой через точку пересечения его с осью ординат?

Составьте уравнение касательной к графику функции f(x) = e ^ x / 3, проведённой через точку пересечения его с осью ординат.

На этой странице сайта размещен вопрос Составьте уравнение касательных к графику функции y = x ^ 8 + 4x ^ 4 — 5 в точках его пересечения с осью абсцисс? из категории Алгебра с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Прямая y=–5x+6 является касательной к графику функции 28x^2+23x+с. Найдите с (профильный ЕГЭ)Скачать

Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке

Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем точке ( x_0 ).

Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).

Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> Введите выражение функции ( f(x)) и число (x_0) — абсциссу точки в которой нужно построить касательную Найти уравнение касательной

Видео:Задание 7 ЕГЭ по математикеСкачать

Немного теории.

Видео:Задача 7 ЕГЭ по математике #2Скачать

Угловой коэффициент прямой

Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом прямой, а угол ( alpha ) — углом между этой прямой и осью Ox

Видео:Что такое касательная | Осторожно, спойлер! | Борис Трушин |Скачать

Уравнение касательной к графику функции

Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.

Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.

С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное равенство: (f(a)=ka+b ), т.е. ( b = f(a) — ka ).

Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:

Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).

Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )

Видео:Геометрический смысл производной | КасательнаяСкачать

Уравнение касательной к графику функции

Онлайн калькулятор для вычисления уравнения касательной к графику функции.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0
задано, то переходим к п.2.
Нахождение производной y'(x).
Вычисление значения производной при x0.
Запись уравнения касательной к кривой линии в форме: yk = y0 + y'(y0)(x — x0)

Калькулятор поможет составить и решить уравнение касательной к графику функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

Видео:Уравнение касательной, параллельной заданной прямой.Скачать

Как составить уравнение касательной к графику функции

Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Видео:Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать

Как составлять уравнение касательной в заданной точке

При написании уравнения будем использовать следующие обозначения:

• x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
• f(x) — исходная функция;
• f'(x) — производная от функции;
• k — угловой коэффициент.

Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.

Алгоритм написания уравнения

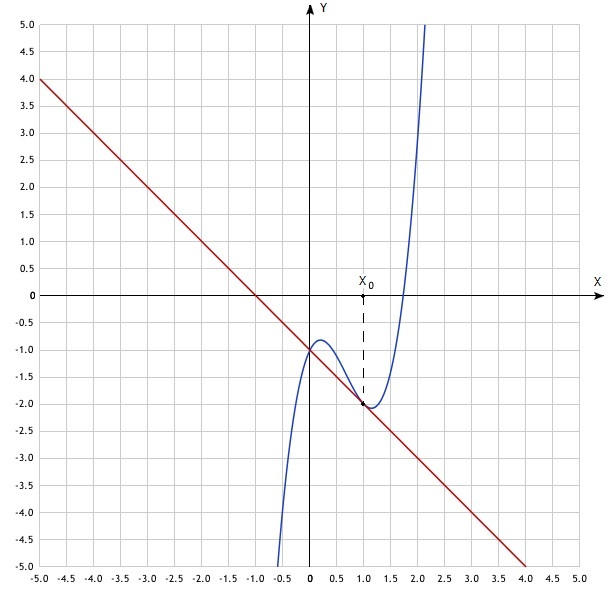
После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:

1. Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
2. Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
3. Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
4. Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.

В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.

Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.

Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.

Видео:Касательная к графику функции в №7 из ЕГЭ по математикеСкачать

Задачи на написание уравнения касательной

Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.

Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.

Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.

• Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
• Возьмем от функции производную: f'(x) = 4x.
• Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
• Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
• Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.

В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.

Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).

• Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
• Запишем производную: g'(x) = 6x².
• Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
• Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
• Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
• В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.

Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.

Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.

Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.

Видео:Как построить график функции без таблицыСкачать

Видео

Закрепить это тему вам поможет видео.