IV. Составить дифференциальное уравнение и найти решение.
Для составления ДУ необходимо вспомнить, в чем состоит геометрический и физический смысл производной.
В физических задачах надо прежде всего решить, какую из величин взять за независимую переменную, а какую – за искомую функцию. Затем надо выразить, на сколько изменится искомая функция у, когда независимое переменное х получит приращение 
, т.е. выразить разность 
через величины, о которых говорится в задаче. Разделив эту разность на и перейдя к пределу при 
, получим ДУ, из которого можно найти искомую функцию. Иногда ДУ можно составить более простым путем, воспользовавшись физическим смыслом производной (если независимое переменное время t, то 
— скорость изменения величины у).
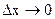
Чтобы решить геометрическую задачу, надо построить чертеж, обозначить искомую кривую через у. Тогда у / — угловой коэффициент касательной, проведенной к искомой кривой. далее надо выразить все упомянутые величины через х, у, у / . Тогда данное в условии задачи соотношение превращается в ДУ, из которого можно найти искомую функцию у(х).
В некоторых задачах содержатся условия, с помощью которых можно определить значения постоянных, входящих в общее решение ДУ.
Примеры
Задача 1. За какое время тело, нагретое до 100 о , охладится до 25 о в комнате с температурой 20 о , если до 60 о оно охладилось за 20 мин. (По закону Ньютона скорость охлаждения тела в воздухе пропорциональна разности температуры воздуха).
Решение. Пусть в момент времени t после начала охлаждения тела его температура будет Т о , тогда, с одной стороны, скорость изменения температуры тела выразится формулой 
. С другой стороны, по закону Ньютона скорость охлаждения тела пропорциональна разности температур тела и воздуха в комнате. т.е. она равна 
, здесь k — коэффициент пропорциональности, зависящий от массы, теплопроводности, формы тела.
Сравнивая оба полученных выражения для скорости изменения температуры, получим:
(знак минус, т.к. как температура тела уменьшается). Получили ДУ первого порядка с разделяющимися переменными. Решая его, получим общее решение:
. (*)
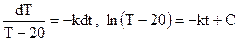
Произвольную постоянную С и коэффициент k можно найти из начальных условий. Подставляя в (*) t=0 мин., Т=100 о , получим 
.
При t=20 мин., Т=60 о , следовательно:
.
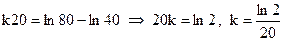
Таким образом, частное решение ДУ, удовлетворяющее всем условиям задачи, будет 
или 
, 
.
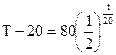
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Теперь выясним, через сколько времени температура тела станет раной 25 о . Подставляя вместо Т число 25, находим t:
.
Следовательно, тело остынет до температуры 25 о через 80 мин.
Задача 2. Найти: 1) семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания; 2) кривую этого семейства, проходящую через точку
Решение. ДУ искомого семейства у / =у или 
. Проинтегрировав обе части равенства, получим 
или 
. Определим значение С, соответствующее начальным значениям:
; 
; 
.
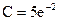
Следовательно, 
— искомая кривая (проходящая через точку Р).
Пример 3.Найти кривые, проходящие через точку N(0, 1), для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 
.
Решение. Пусть точка М с координатами (х, у) принадлежит искомой кривой (рис. 1). Тогда МА – отрезок касательной к кривой , причем 
.
|
. По условию 
. Отсюда 
. 
У
М(х, у)
Это дифференциальное уравнение с разделяющимися переменными. Решая его, получим:
.
Учитывая, что кривые проходят через точку N(0, 1), найдем величину С:
, 
.
Следовательно, уравнения искомых кривых имеет вид
.
Задание №5 для контрольной работы.
5.1. Найти кривую, проходящую через точку (4, 4), для которой угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.
5.2. Найти уравнение кривой, для которой отрезок касательной между точкой касания и осью ОХ делится пополам в точке пересечения с осью ОY. Известно, что искомая кривая проходит через точку Р(1, 2).
5.3. Найти линию, проходящую через точку Мо(6, 4) и обладающую тем свойством, что в любой ее точке М нормальный вектор 
с концом на оси ОY имеет длину, равную а=10, и образует острый угол с положительным направлением оси ОY.
5.4. Найти линию, проходящую через точку Мо(1, 1), если отрезок любой ее нормали, заключенный между осями координат, делится точкой линии в соотношении 1:2 (считая от оси OY).
Видео:Математика без Ху!ни. Уравнение касательной.Скачать
5.5. Найти линию, проходящую через точку Мо(2, -1), если отрезок любой ее касательной между точкой касания и осью ОY делится в точке пересечения с осью абсцисс в соотношении 1:1.
5.6. Найти линию, проходящую через точку Мо(1, 2), если отрезок любой ее касательной, заключенной между осями координат, делится в точке касания в соотношении 1:1.
5.7. Найти линию, проходящую через точку Мо(2, е) и обладающую тем свойством, что в любой ее точке М касательный вектор с концом на оси ОХ имеет проекцию на ось ОХ обратно пропорциональную абсциссе точки М. Коэффициент пропорциональности k равен -2.
5.8. Найти кривую, проходящую через точку Мо(4, 3), у которой подкасательная есть среднее арифметическое координат точек касания М (подкасательная ТР, где точка Р – проекция точки М на ось ОХ, точка Т – точка пересечения касательной с осью ОХ).
5.9. Найти линию, проходящую через точку Мо(1, 1) и обладающую тем свойством, что в любой ее точке М касательный вектор с концом на оси ОY имеет проекцию на ось ОY, равную 1.
5.10. Найти кривую, для которой сумма длин отрезка касательной к подкасательной пропорциональна произведению координат точки касания М. Кривая проходит через точку Мо(1, 1), коэффициент пропорциональности 
(подкасательная ТР, где точка Р – проекция точки М на ось ОХ, точка Т – точка пересечения касательной с осью абсцисс).
5.11. Пользуясь прямоугольными координатами, найти форму зеркала, собирающего все параллельные лучи в одну точку. Взять падающие лучи параллельными оси ОХ.
5.12. Составит уравнение кривой, проходящей через точку Мо(а, а) и обладающей следующим свойством: если в любой точке М(х, у) кривой с ординатой РМ провести касательную до пересечения с осью ОY в точке Т, то площадь трапеции ОТМР равна .
5.13. Площадь треугольника, образованного радиус-вектором ОМ любой точки М(х, у) кривой, касательной МР к этой точке и осью ОХ, равна 2. Кривая проходит через точку Мо(2, -2). Найти уравнение этой кривой.
5.14. Составить уравнение кривой, проходящей через начало координат, зная, что середина отрезка ее нормали от любой точки кривой М до оси ОХ находится на параболе 
.
5.15. Определить кривую, проходящую через точку Мо(1, 1), у которой отрезок касательной от точки касания М до пересечения с осью ОХ равен отрезку ОТ, где точка Т – точка пересечения касательной с осью ОХ.
5.16. Найти уравнение кривой, проходящей через точку Мо(1, 1) и обладающей тем свойством, что отрезок, отсекаемый касательной на оси ординат равен квадрату абсциссы точки касания.
5.17. Найти кривую, проходящую через точку Мо(3, 0), у которой отрезок, отсекаемый касательной на оси ординат, равен полусумме координат точки касания.
5.18. Найти кривую, проходящую через точку Мо(1, 1) и обладающую тем свойством, что величина перпендикуляра, опущенного из начала координат на касательную, равна абсциссе точки касания.
5.19. Найти кривую, проходящую через точку Мо(1, 1) и обладающую тем свойством, что отрезок, который касательная в любой точке кривой отсекает на оси ОY равна квадрату абсциссы точки касания.
Видео:Составить дифференциальные уравнения семейств линийСкачать
5.20. Определить кривую, проходящую через точку Мо(0, 1), у которой отношение отрезка, отсекаемого касательной на оси ОY, к радиус-вектору равна 1.
5.21. Найти кривую, у которой подкасательная имеет постоянную длину а. Кривая проходит через точку Мо(а, е) (подкасательная ТР, где точка Р – проекция точки М на ось ОХ, точка Т – точка пересечения касательной с осью абсцисс).
5.22. Найти кривую, проходящую через точку Мо(2, 1), для которой подкасательная равна среднему арифметическому координат точки касания.
5.23. Найти уравнение кривой, проходящей через точку Мо(3, 5) и обладающую тем свойством, что в любой точке М нормальный вектор с концом на оси ОY имеет длину, равную 5, и образует острый угол с положительным направлением оси ОY.
5.24. Найти кривую, проходящую через точку Мо(1, 4) и обладающую тем свойством, что в любой ее точке М касательный вектор с концом на оси ОY имеет проекцию на ось ОY, равную 2.
Раздел 6
КРАТНЫЕ ИНТЕГРАЛЫ
1. Двойной интеграл
1.1. Задача об объеме цилиндрического тела.
1.2. Двойной интеграл и его основные свойства.
1.3. Вычисление двойных интегралов в декартовых координатах.
1.4. Замена переменных в двойном интеграле. Переход от декартовых координат к полярным.
Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать
1.5. Приложение двойного интеграла для решения задач геометрии и физики.
Литература 
, гл. ХIV, §1, 2, упр. 1, 4-6; §3, упр. 8-10, 15, 17; §4, упр. 24, 25, 32; §5, 6, упр. 18-20, 28; §7, упр. 43, 46, 48; §9, упр.59, 60; §10, упр. 53, 54.
Вопросы для самопроверки
1. Что называется двойным интегралом от функции f(x; y) по области D? Укажите его геометрический смысл.
2. Сформулируйте теоремы о двойном интеграле от суммы и вынесении постоянного множителя за знак двойного интеграла. Докажите, что
, где 
.
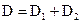
3. Что называется двукратным интегралом от функции f(x; y) по области D? Как он вычисляется?
4. Докажите теорему о среднем для двойного интеграла, укажите ее геометрический смысл.
5. Выведите формулу для вычисления двойного интеграла с помощью двукратного. Дайте геометрическое толкование формулы в случае неотрицательной подынтегральной функции.
6. Обоснуйте формулы, служащие для вычисления объема цилиндрического тела и площади плоской фигуры с помощью двойных интегралов.
7. Выведите формулу для вычисления двойного интеграла в полярных координатах.
8. Каков геометрический смысл интеграла
,
где z=z(x; y) – функция, обладающая непрерывными частными производными в области D?
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
9. Каков механический смысл интеграла
,
где 
— непрерывная функция в области D?
10. Выведите формулу для вычисления координат центра тяжести плоской фигуры D, поверхностная плотность которой 
.
Тройной интеграл
2.1. Тройной интеграл и его основные свойства.
2.2. Вычисление тройных интегралов в декартовых координатах.
2.3. Замена переменных в тройном интеграле. Использование цилиндрических и сферических координат.
2.4. Геометрические и механические приложения тройных интегралов.
Литература , гл. ХIV, §11, 12, упр. 65, 66; §13, упр. 67; §14, упр. 68, 69.
Вопросы для самопроверки
1. Что называется тройным интегралом от функции f(x, y, z) пространственной области V? Укажите его механический смысл.
2. Что называется трехкратным интегралом от функции f(x, y, z) по области V? Как он вычисляется?
3. Сформулируйте теорему о среднем для тройного интеграла.
Видео:Составить дифференциальное уравнение семейства кривыхСкачать
4. Выведите формулу для вычисления тройного интеграла с помощью трехкратного. Напишите формулу для вычисления тройного интеграла в цилиндрических координатах.
5. Обоснуйте формулу, служащую для вычисления объема тела с помощью тройного интеграла.
6. Каков механический смысл интеграла
,
где 
— непрерывная функция в области V? Напишите формулы для вычисления координат центра тяжести тела V, объемная плотность которого 
.
📺 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Геометрический смысл производной. Уравнение касательнойСкачать
Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать
Как распознать талантливого математикаСкачать
Уравнение плоскости. 11 класс.Скачать
Математика это не ИсламСкачать
Составить дифференциальное уравнение окружностей R = 1, с центром на прямой y = 2xСкачать
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать
Откуда появляются дифференциальные уравнения и как их решатьСкачать
Уравнение касательной к кривой.Скачать
1. Что такое дифференциальное уравнение?Скачать
Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать
