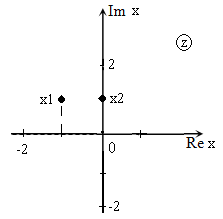Составление квадратного уравнения по комплексным корням

Видео:Комплексные корни квадратного уравненияСкачать

Квадратное уравнение с комплексными корнями и коэффициентами

Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты $a$, $b$ и $c$ — в общем случае являются комплексными. Его решение находим с помощью дискриминанта

В общем случае и дискриминант, и корни уравнения являются комплексными числами.

Задание. Составить квадратное уравнение, которое имеет корни $z_=1-i$ и $z_=4-5i$. Решить его.

Решение. Известно, что если $z_1$, $z_2$ — корни квадратного уравнения $z^2+bz+c=0$, то указанное уравнение можно записать в виде $(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом:

Раскрываем скобки и выполняем операции над комплексными числами:

$z^+(-5+6 i) z-(1+9 i)=0$ — искомое квадратное уравнение.

Решим полученное уравнение. Найдем дискриминант:

$$D=(-5+6 i)^-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$ $$=-7-24 i$$

Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде $sqrt=a+b i$. То есть

$$sqrt=a+b i Rightarrow-7-24 i=(a+b i)^ Rightarrow$$ $$Rightarrow-7-24 i=a^+2 a b i-b^$$

Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений $a$ и $b$:

решив которую, имеем, что $a_1=3$, $b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из полученных пар, например, первую, получаем, что $sqrt=3-4 i$, а тогда

Ответ. $z^+(-5+6 i) z-(1+9 i)=0$

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ =8$.

Так как $A>0$, то $x_ =sqrt[] cdot left(cos frac +icdot sin frac right),, , , k=0. 2$.

При $k=0$ получаем $x_ =sqrt[] cdot left(cos 0+icdot sin 0right)=sqrt[] =2$.

При $k=1$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac +frac <sqrt> cdot i)=2cdot (-frac +frac <sqrt> cdot i)=-1+sqrt cdot i.]

При $k=2$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac -frac <sqrt> cdot i)=2cdot (-frac -frac <sqrt> cdot i)=-1-sqrt cdot i.]

Решить уравнение: $x^ =1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac =arctg1=frac ]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ =sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] cdot left(cos frac +icdot sin frac right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ -4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

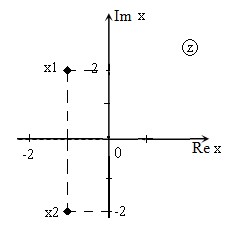
Решить уравнение $x^ +2x+5=0$ и изобразить корни на плоскости.

[D=2^ -4cdot 1cdot 5=4-20=-16.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ $ являются корнями квадратного уравнения $ax^ +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ )(x-x_ )=0$. В общем случае $x_ $ являются комплексными корнями.

Зная корни уравнения $x_ =1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ -x+2icdot x-x-2icdot x+1-4i^ =0] [x^ -2x+1+4=0] [x^ -2x+5=0]

Следовательно, $x^ -2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Презентация к уроку по математике на тему «Решение квадратных уравнений с помощью комплексных чисел» 1 курс специальность «Мастер по лесному хозяйству»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Решение квадратных уравнений с помощью комплексных чисел

«Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием». Г. Лейбниц

Термин “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века — Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа i(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово «комплекс» (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. образующих единое целое.

Н. Н. Богомолов и В. С. Владимиров — к проблемам квантовой теории поля. Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые: Н. И. Мусхелишвили занимался ее применениями к теории упругости; М. В. Келдыш и М. А. Лаврентьев — к аэро- и гидродинамике;

Обозначение: – алгебраическая форма записи комплексного числа Комплексным числом называется число вида a+ib , где a, b − некоторые действительные числа, а i− мнимая единица, при чем:

Множество комплексных чисел обозначается С, N Z Q I R C

Число a называется действительной частью комплексного числа z. Обозначается a=Re z. Число b называется мнимой частью комплексного числа z. Обозначается b=Im z.

Мнимая ось Действительная ось 0 1 1 a b M(a; b) z=a+jb

Примеры: 1) Изобразите комплексные числа

2) Запишите комплексные числа, изображенные на координатной плоскости, в алгебраической форме. 0 1 1 -2 4 3 2 -3 -4 -5

3) На какой из координатных плоскостей изображено число 0 1. 2. 3. 4. 0 0 0

Степени мнимой единицы По определению: Таким образом, можно вывести формулу для вычисления

Исследование алгебраических уравнений является одним из важнейших вопросов математики. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение x²+1=0 Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения x²=-1 Обозначим этот корень через i,тогда по определению i²+1=0 i²=-, а следовательно i=√-1

На множестве С можно находить корни любых квадратных уравнений! Как извлечь квадратный корень из отрицательных действительных чисел? Решение квадратных уравнений с действительными коэффициентами и D

Краткое описание документа:

Урок на тему: «Решение квадратных уравнений с помощью комплексных чисел».

Цели:

Образовательные: расширить понятие числа, ввести понятие комплексного числа, действия над комплексными числами, заданными в алгебраической форме.

Воспитательные: прививать интерес к математике, ознакомить учащихся с историей развития комплексных чисел, воспитывать

Развивающие: развивать творческое мышление, пространственное мышление, научить применять теоретические знания при решении практических задач, формировать активность и самостоятельность при работе в группах.

Используемые технологии и методы: 1) проблемный диалог; 2) информационно- коммуникационные технологии.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 932 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:10 класс, 35 урок, Комплексные числа и квадратные уравненияСкачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 575 681 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 11.08.2018
• 207
• 0

• 11.08.2018
• 366
• 2

• 11.08.2018
• 441
• 1

• 11.08.2018
• 1407
• 30

• 11.08.2018
• 355
• 0

• 11.08.2018
• 648
• 2

• 10.08.2018
• 911
• 25

• 10.08.2018
• 598
• 6

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 11.08.2018 1750
• PPTX 1.6 мбайт
• 73 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Ломова Людмила Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 14460
• Всего материалов: 21

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Минобрнауки создаст для вузов рекомендации по поддержке молодых семей

Время чтения: 1 минута

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎦 Видео

Решение квадратных уравнений в поле комплексных чиселСкачать

@Квадратные уравнение в комплексных числах #математикаСкачать

Биквадратное уравнение. Комплексные корни.Скачать

Комплексные числа в уравненияхСкачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Как применять формулу корней квадратного уравненияСкачать

Составьте квадратное уравнение, корнями которого являются числаСкачать

Алгебра. Раздел 7. Тема 7. Составление квадратного уравнения по его корнямСкачать

Составление квадратных уравнений с помощью заданных корнейСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Извлечение квадратного корня из комплексного числа. 11 класс.Скачать

Решение квадратных уравнений с помощью теоремы Виета. Как составить кв. уравнение по его корнямСкачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать