Составление дифференциальных уравнений семейства кривых

Видео:Составить дифференциальные уравнения семейств линийСкачать

Составление уравнений семейства кривых

Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства:

φ (1)

необходимо продифференцировать равенство (1) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (1) исключить произвольные постоянные C₁ … C_n.

Линии, пересекающие все кривые данного семейства под одним и тем же углом ϕ, называются изогональными траекториями . Углы β и α наклона траектории и кривой к оси Ox связаны соотношением β = α ± φ.

— дифференциальное уравнение данного семейства кривых, а

— уравнение семейства изогональных траекторий.

Тогда tg α = f (x,y), tg β = f₁ (x,y).

Отсюда следует, что если дифференциальное уравнение семейства кривых написано и угол φ известен, то найти tg β не составит труда, а после также легко можно будет написать уравнение траекторий.

Частный случай:

Если уравнение семейства кривых записано в виде:

,

то при составлении уравнения траекторий можно обойтись без решения уравнения относительно y’, в этом случае будет достаточно y’ заменить на tg α = tg (β ± φ), где tg β = y’ — угловой коэффициент касательной к траектории.

Пример №1

Составить дифференциальное уравнение семейства кривых:

• Так как уравнение содержит два параметра (С₁ и С₂), то и дифференцировать будем два раза:

Первая производная:

Вторая производная:

• Дальше, чтобы составить дифференциальное уравнение семейства кривых необходимо избавиться от С₁ , а для этого выведем его из уравнения первой производной С₁ = -2(y — С₂)y’ и подставим в наше уравнение:

(2)

• Теперь также нужно избавиться от параметра C₂, а для этого выведем ее из второй производной: y — C₂ = -y’ 2 / y» и подставим это в (2):

• Ну и наконец упростим полученное уравнение и получим:

Пример №2

Для закрепления составим еще одно уравнение:

Решение абсолютно идентично предыдущему, за исключением того, что вместо параметров С₁ и С₂ здесь представлены параметры a, b и с. Ну и, конечно, раз параметров три, то нам понадобятся производные первого, второго и третьего порядка.

Делать описание каждого шага я уже не буду, думаю вы уже сами разберетесь:

Первая производная:

Вторая производная:

Третья производная:

Ответ:

Ну, думаю, если вы разобрались в первыми двумя примерами, то все остальные вы решите без труда, а чтобы это проверить дам вам парочку заданий «на дом».

Пример №3

Выразим коэффициенты a и b через 1-ую и 2-ую производные:

Первая производная: , где

Вторая производная: , где

Подставим значение b второй производной в значение a первой производной:

А теперь подставим полученные значения a и b в исходное уравнение и упростим:

⇒

Ответ:

Пример №4

Ну а здесь все еще проще:

Возведем обе части уравнения в квадрат:

Чтобы воспользоваться основным тригонометрическим тождеством, вычтем из единицы обе части уравнения:

Ну и теперь как мы видим во второй части получилось исходное уравнение, только в квадрате, а значит оно будет равно:

Приведем к общему виду и запишем ответ:

Ответ:

Ну и на этой ноте мы с вами закончим данный урок, всем спасибо!

Если вам что-то непонятно (или нашли неточности в уроке) пишите в комментариях и мы вам обязательно ответим в ближайшее время.

Видео:2. Дифференциальное уравнение семейства кривыхСкачать

Составление дифференциальных уравнений семейств линий

Пусть дано уравнение однопараметрического семейства плоских кривых

Дифференцируя (1) по , найдем

Исключая параметр из (1) и (2), получаем дифференциальное уравнение

выражающее свойство, общее всем кривым семейства (1). Уравнение (3) будет искомым дифференциальным уравнением семейства (1).

Если однопараметрическое семейство кривых определяется уравнением

то дифференциальное уравнение этого семейства получим, исключая параметр из уравнений

Пусть теперь имеем соотношение

где — параметры. Дифференцируя (4) раз по и исключая параметры из (4) и полученных уравнений, приходим к соотношению вида

Это дифференциальное уравнение заданного n-параметрического семейства линий (4) в том смысле, что (4) есть общий интеграл уравнения (5).

Пример 1. Найти дифференциальное уравнение семейства гипербол .

Решение. Дифференцируя это уравнение по , получаем

Умножим обе части на , тогда . Подставляя в уравнение семейства найдем .

Пример 2. Найти дифференциальное уравнение семейства линий , где — параметр.

Решение. Дифференцируем обе части уравнения по :

Из выражения для находим
и, подставляя это выражение для в уравнение семейства линий, получим

Пример 3. Составить дифференциальное уравнение семейства прямых, отстоящих от начала координат на расстояние, равное единице.

Решение. Будем исходить из нормального уравнения прямой

Дифференцируя (6) по , найдем , откуда , следовательно,

Подставив и в (6), получим

Видео:Составить дифференциальное уравнение семейства кривыхСкачать

2°. Задачи на траектории

Пусть дано семейство плоских кривых, зависящее от одного параметра ,

Кривая, образующая в каждой своей точке постоянный угол с проходящей через эту точку кривой семейства (7), называется изогональной траекторией этого семейства; если, в частности, , то — ортогональной траекторией .

Считая семейство (7) заданным, будем разыскивать его изогональные траектории.

А. Ортогональные траектории . Составляем дифференциальное уравнение данного семейства кривых (см. п. 1). Пусть оно имеет вид

Дифференциальное уравнение ортогональных траекторий имеет вид

Общий интеграл этого уравнения дает семейство ортогональных траекторий.

Пусть семейство плоских кривых задано уравнением в полярных координатах

получаем дифференциальное уравнение семейства ортогональных траекторий

Б. Изогональные траектории . Пусть траектории пересекают кривые данного семейства под углом , причем . Можно показать, что дифференциальное уравнение изогональных траекторий имеет вид

Пример 4. Найти ортогональные траектории семейства линий .

Решение. Семейство линий состоит из прямых, проходящих через начало координат. Для нахождения дифференциального уравнения данного семейства дифференцируем по обе части уравнения . Имеем . Исключая параметр из системы уравнений будем иметь дифференциальное уравнение семейства . Заменяя в нем на , получаем дифференциальное уравнение ортогональных траекторий , или . Полученное уравнение является уравнением с разделяющимися переменными; интегрируя его, найдем уравнение ортогональных траекторий . Ортогональными траекториями являются окружности с центром в начале координат (рис. 15).

Пример 5. Найти уравнение семейства линий, ортогональных к семейству .

Решение. Данное семейство линий представляет собой семейство окружностей, центры которых находятся на оси и которые касаются оси .

Дифференцируя по обе части уравнения данного семейства, найдем . Исключая параметр из уравнений получаем дифференциальное уравнение данного семейства . Дифференциальное уравнение ортогональных траекторий есть

Это уравнение является однородным. Интегрируя его, найдем . Интегральные кривые являются окружностями, центры которых расположены на оси и которые касаются оси (рис. 16).

Пример 6. Найти ортогональные траектории семейства парабол .

Решение. Составляем дифференциальное уравнение семейства парабол. Для этого дифференцируем обе части данного уравнения по . Исключая параметр , найдем , или дифференциальное уравнение данного семейства. Заменяя в уравнении на , получим дифференциальное уравнение ортогональных траекторий

Интегрируя, найдем или 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAJUAAAAuBAMAAADTgUbKAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAmsOBAetBIBAxYUJRcbGvhmSvAAACYklEQVRIx2NgGOTgoNIEahnFrsEYQC2z2L6xfaOaHxN4vlMvwJgEqGfWReoZxSXQQZU4nMAxgWEygyUVjOJQVFz3kD3+/wcqmOU3IV8l3iMtLYEKZiUy5K/Qolq42xdQzSgWVQfcgWlMkte5OT4ylOGS7KsJJsUs+TN/GaxxSV4tsCfFLKEiZV+c+Wdew3osgeKC0xuSjfiiUQgzDBfFa3MtQBXzTiEmNMMxhI7qODTJo5acPIGi2OOIC5lT1IAuzfgXmO2+okZ96QGucOylD5I6DglmdMPuGwBDTA/I4BSHB6A8A8tHgmY1CZuie/oriNQFEUlww4IccCRSqFnsjyYwnFmkpIgm6/QLREJM2acNUcryyYFFH59ZfUUKLIGwYikNDEABPv8HktJCiGGcILMa8Jh1y/UB51+oEKcxGBwABZcCklKXwiiQYrZPDAz6GxgYFgrCAcjhXMbGpkBdQEtWnF/A+xNLQQBK1xxwbrEOKAwJmcUg38AUgsUsA5DT4SVLM8gsDkLhxRDE4P8Aix9B7poIDzAtkGIWQvHI8pkh/wIs7HeDASjs64H1O4c6zCgd4tIXMBLfY2lj8H50YJgEFd8ITRMM+xNwVPswPy4VCsXm7qWBRlBnJUnDs13s1QXw0tMci1ke2wOxFsN7j0MDURwhWLUcxpq0Vn8BRt4uVWAmp4kRydCKmZLyDfYvIKPi/t/A/BlDlFHpGTk1d2gD8ydMYReyajUXBsbP1GvmtEZQzyxRqrV8GbgiqeesqRM4qWUUpwYi51PsrGNpwlQyikP///8/1PKikpKSJuXGAACuZpWkdXHGfwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Ортогональным семейством является семейство эллипсов (рис. 17).

Пример 7. Найти ортогональные траектории семейства лемнискат .

Решение. Имеем . Исключая параметр , получим дифференциальное уравнение данного семейства кривых Заменяя на , найдем дифференциальное уравнение семейства ортогональных траекторий откуда . Интегрируя, находим уравнение ортогональных траекторий

Ортогональными траекториями семейства лемнискат являются лемнискаты, ось симметрии которых образуют с полярной осью угол (рис. 18).

Видео:Огибающая семейства кривых | Дифференциальные уравненияСкачать

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Видео:Практика 1 ИзоклиныСкачать

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

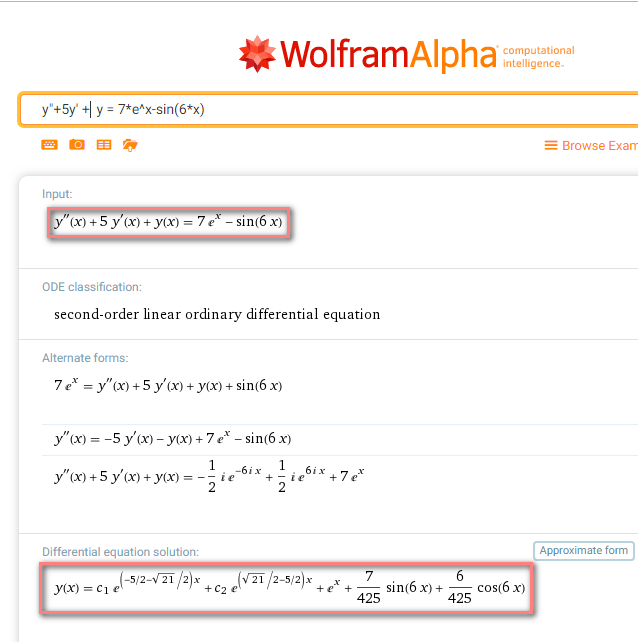
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Видео:1. Что такое дифференциальное уравнение?Скачать

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Видео:Дифференциальные уравнения. 11 класс.Скачать

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+cos x, quad y(0)=0, y'(0)=0, y»(0)=0. $$

Видео:Особые решения дифференциальных уравнений, огибающая семейства кривых | Лекция 34 | МатанализСкачать

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=frac<9e^><3+e^>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$

Видео:Составление дифференциального уравненияСкачать

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Видео:1.1. Составление имитационной модели в виде дифференциального уравненияСкачать

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

🔥 Видео

Как распознать талантливого математикаСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Составление и линеаризация дифференциального уравнения центробежного маятникаСкачать

Асташова И. В. - Дифференциальные уравнения I -Семинар 2Скачать