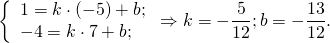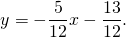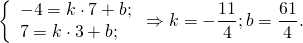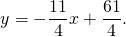Составить уравнения сторон треугольника если даны одна из его вершин и уравнения двух биссектрис (3 видео)

Задача 41599 Составить уравнения сторон треугольника.

Содержание

Условие
Все решения
Уравнения сторон треугольника
Составить уравнения сторон треугольника если даны одна из его вершин и уравнения двух биссектрис
📺 Видео

Условие

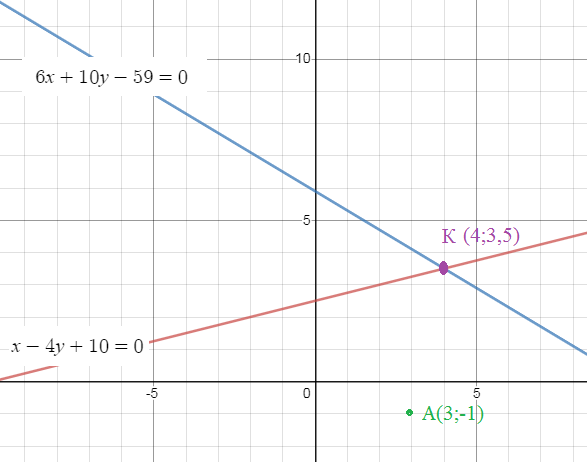
Составить уравнения сторон треугольника, зная одну его вершину A(3;-1), а также уравнения биссектрисы x-4y+10=0 и медианы 6x+10y-59=0, проведенных из различных вершин.

Все решения

Найдем координаты точки пересечения биссектрисы и медианы:
<x–4y+10=0
<6x+10y–59=0

Умножаем первое уравнение на (-6)
<-6x+24y-60=0
<6x+10y–59=0
Складываем
34у=119
y=3,5
x=4y-10=4*3,5-10=4

точка имеет координаты (4;3,5) Обозначим ее[b] К ( 4;3,5) [/b]

Составим уравнение прямой AК, как прямой проходящей через две точки:

[b]9x-2y-29=0 [/b] — уравнение [b]прямой АК[/b]

Видео:Уравнения стороны треугольника и медианыСкачать

Уравнения сторон треугольника

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

Таким образом, уравнение стороны AB

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

Отсюда уравнение стороны BC —

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

Видео:найти уравнения биссектрис углов между прямымиСкачать

Составить уравнения сторон треугольника если даны одна из его вершин и уравнения двух биссектрис

Даны уравнения высот треугольника 2x — 3y + 1 = 0 и x + y = 0 и координаты одной из его вершин A(1, 2). Найти уравнения сторон треугольника.

Точка A(1, 2) не принадлежит данным в условии высотам треугольника, так как ее координаты не удовлетворяют их уравнениям: и . Отсюда следует, что высоты, данные в задаче, проведены из двух других вершин треугольника B и C (см. рисунок)

Назовем их CD и BE, CD AB, BE AC. Пусть высота CD имеет уравнение x + y = 0, а уравнение высоты BE 2x — 3y + 1 = 0. Так как AC BE, то уравнение AC мы найдем из уравнения семейства прямых, перпендикулярных BE, приняв во внимание, что искомая прямая проходит через данную точку A(1, 2).

Сторона AC имеет уравнение 3x + 2y — 7 = 0. Уравнение прямой AB найдем, как уравнение прямой, проходящей через точку A(1, 2) перпендикулярно CD. Оно имеет вид

Теперь следует найти координаты точек B и C:

Уравнение стороны BC 2x + 3y + 7 = 0.

Таким образом, уравнения всех трех сторон треугольника найдены.