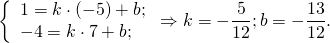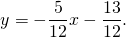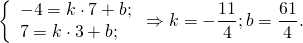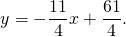Видео:Вычисляем высоту через координаты вершин 1Скачать
Задача 36077 Помогите, пожалуйста, с задачей. Даны.
Условие
Помогите, пожалуйста, с задачей. Даны уравнения сторон прямоугольника 3х-4у+5=0, 4х+3у-7=0 и одна из его вершин А(-2;1). Составить уравнения двух других сторон прямоугольника.
Решение
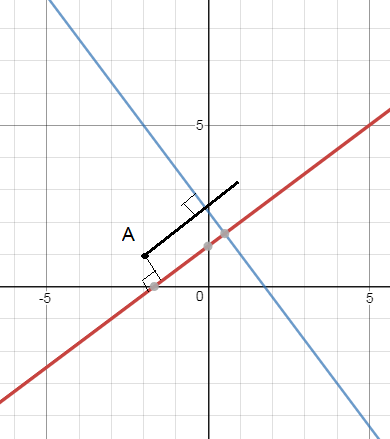
Очевидно, что точка А не принадлежит ни одной из данных сторон, подставляем ее координаты в уравнение и убеждаемся, что координаты не удовлетворяют ни первому , ни второму уравнению
3*(-2)-4*1+5=0- неверно
4*(-2)+3*1-7=0 -неверно
Так как прямые
3х–4у+5=0 и 4х+3у–7=0
пересекаются под прямым углом, то дальнейшее решение видно из рисунка.
На рисунке проводим через точку А две прямые, перпендикулярные данным ( или параллельные данным как хотите)
Можно и так и так.
Находим уравнение прямой перпендикулярной
3х–4у+5=0
y=(3/4)x+(5/4)
k=3/4
Значит k=-4/3 — угловой коэффициент перпендикулярной прямой
y=(-4/3)x+b
Чтобы найти b подставляем координаты точки А
1=(-4/3)*2+b
b=11/3
y=(-4/3)x+(11/3)
[b]4x+3y-11=0[/b]
Находим уравнение прямой перпендикулярной
4х+3у–7=0
y=(-4/3)x+(7/3)
k=-4/3
Значит k=3/4 — угловой коэффициент перпендикулярной прямой
y=(3/4)x+b
Чтобы найти b подставляем координаты точки А
1=(3/4)*2+b
b=-1/2
y=(3/4)x+(-1/2)
[b]3x-4y-1=0[/b] 
Видео:Уравнения стороны треугольника и медианыСкачать
Уравнения сторон треугольника
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. 📹 ВидеоУравнение прямой и треугольник. Задача про высотуСкачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Математика без Ху!ни. Уравнение плоскости.Скачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Уравнение плоскости через 3 точкиСкачать  Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать  11. Прямая в пространстве и ее уравненияСкачать  Составляем уравнение прямой по точкамСкачать  Написать канонические и параметрические уравнения прямой в пространствеСкачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  №972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать  Аналитическая геометрия на плоскости. Решение задачСкачать  №568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать  | ||