Составить уравнение сферы если точки являются концами одного из диаметров

Глава VI. Простейшие криволинейные поверхности и тела вращения.

Задачи к главе VI

6.1. Напишите уравнение сферы с центром в начале координат и радиусом R = 6.

6.2. Точка М(—2; 2; 1) лежит на сфере, а центр сферы находится в начале координат. Составьте уравнение сферы.

6.3. Дана сфера х 2 + у 2 + z 2 = 9 и три точки: А(2; —1; 1), B(2; 2; —1), С(—1; —2; 5). Установите, какая из этих точек находится внутри сферы, лежит на сфере, находится вне сферы.

6.4. Найдите центр и радиус сфер:

6.5. Докажите, что следующие уравнения являются уравнениями сфер:

6.6. Какая фигура является пересечением сферы х 2 + у 2 + z 2 = 1 в плоскости:

6.7. Какая фигура является пересечением сферы х 2 + у 2 + z 2 = 10 и плоскости z = 1?

6.8. Плоскость z = — 1 пересекает сферу (х — 1) 2 + (у — 2) 2 + (z — 3) 2 = 25 по некоторой окружности. Найдите ее центр и радиус.

6.9. Центр сферы находится на плоскости z = 4, а сама сфера касается плоскости хОу в точке M (2; 3; 0). Составьте уравнение сферы и определите координаты ее центра.

6.10. Точки A(3; —5; 6) и В (5; 7; —1) являются концами одного из диаметров сферы. Составьте уравнение этой сферы.

6.11. Даны точки: А(2; —5; 8), В(8; —2; 5), С(5; —8; 2) и D (—2; —8; —5). Составьте уравнение сферы, если известно, что эти точки лежат на ее поверхности.

6.12. Найдите координаты точки, симметричной центру сферы
(х — 3) 2 + (у + 2) 2 + (z — 1) 2 = 24 относительно касательной плоскости к сфере в точке
M (—1; 0; 3).

6.13. Точки А (7; —2; 4) и В (9; —8; 6) лежат на поверхности сферы и на прямой, проходящей через ее центр. Составьте уравнение сферы.

6.14. Составьте уравнение поверхности вращения эллипса вокруг оси Oy.

6.15. Эллипс с полуосями а = 6, b = 4 и центром в начале координат вращается вокруг своей большой оси, совпадающей с осью Оz. Составьте уравнение поверхности вращения. Изобразите поверхность на рисунке.

6.16. Составьте уравнение поверхности, описываемой гиперболой при ее вращении вокруг своей действительной оси, совпадающей с осью Ох. Полуоси гиперболы
a = 8 и b= 6, а центр ее совпадает с началом координат. Изобразите поверхность на рисунке.

6.17. Составьте уравнение поверхности вращения гиперболы вокруг оси Оz. Изобразите поверхность на рисунке.

6.18. Составьте уравнение поверхности вращения параболы у 2 = 6z вокруг оси Oz. Изобразите поверхность на рисунке.

6.19. Составьте уравнение поверхности вращения прямой х — 3 = 0 вокруг оси Oz. Изобразите поверхность на рисунке.

6.20. Составьте уравнение поверхности вращения прямой вокруг оси
Ох.

6.21. Составьте уравнение цилиндрической поверхности, у которой направляющая лежит в плоскости хОу и имеет уравнение , а образующая параллельна вектору a (1; 0; 1).

6.22. Какие поверхности определяются уравнениями:

6.23. Кривая в пространстве задана параметрическими уравнениями

Составьте уравнение конической поверхности с вершиной в начале координат, для которой данная кривая является направляющей.

6.24. Составьте уравнение конической поверхности, полученной вращением двух пересекающихся прямых: вокруг оси Оz.

6.25. Установите вид поверхности 14х = у 2 + z 2 и постройте ее изображение.

6.26. Определите, какая поверхность задана уравнением и установите, по какой линии она пересекается с плоскостью z — 1 = 0.

6.27. Определите, какая поверхность задана уравнением и установите, по какой линии она пересекается с плоскостью z + 2 = 0.

6.28. Определите, какая поверхность задана уравнением х 2 + у 2 — 4z= 0, и установите, по какой линии она пересекается с плоскостью х — 2 = 0.

Практическая часть №4

Модуль 9. Практическая часть №4 .

Задача 1: Из точки М, взятой на сфере радиусом 30 см, проведены две взаимно перпендикулярные хорды МА и МВ длиной 24 см и 10 см. На каком расстоянии от центра сферы находится хорда АВ?

Задача 2*: В цилиндр, вписанный в сферу, вписана сфера. Найти отношение радиусов сфер.

(Ответ: :1 )

Задача 3: Написать уравнение сферы с центром в начале координат и радиусом R=6.

Задача 4: Точка М(-2, 2, 1) лежит на сфере, а центр сферы находится в начале координат. Составить уравнение

сферы. (Ответ: x2+y2+z2=9)

Задача 5: Дана сфера x2+y2+z2=9 и три точки

А(2, -1, 1 ), В(2, 2, -1), С(-1, -2, 6). Установить, какая из этих точек находится внутри сферы, лежит на сфере,

вне сферы. ( Ответ: А, В, С )

Задача 6: Найти центр и радиус сферы:

Задача 7: Доказать, что следующие уравнения являются уравнениями сфер:

а) x2+y2+2y+z2+z-1 = 0

б) x2+y2+z2-8x+4y+2z-43 = 0

Задача 8: Какая фигура является пересечением сферы x2+y2+z2 =1 и плоскости:

а) y=1 б) y=1/2 в) y=2

Задача 9: Плоскость z=-1 пересекает сферу

(x-1)2+(y-2)2+(z-3)2=25 по некоторой окружности. Найти ее центр и радиус. ( Ответ: (1,2,-1), R=3)

Задача 10: Точки А( 3,-5,6 ) и В( 5,7,-1 ) являются концами одного из диаметров сферы. Составить уравнение этой сферы.

Задача 11*: Найти координаты точки, симметричной центру сферы (x-3)2+(y+2)2+(z-1)2=24 относительно касательной плоскости к сфере в точке М(-1,2,5).

1. Радиусы шаров равны 25 дм и 29 дм, а расстояние между их центрами 36 дм. Найти длину окружности, по которой пересекаются их поверхности.

2*. В конус, вписанный в сферу, вписана сфера. Найти отношение радиусов сфер, если образующая конуса наклонена к плоскости основания

под углом а. ( Ответ: ctg а/2 (sin 2а) )

3. Какая фигура является пересечением сферы

x2+y2+z2=10 и плоскости z=1?

( Ответ: окружность x2 +y2 = 9, z=1 )

4*. Даны точки А(2,-5,8 ), В(8,-2,5), С(5,-8,2),

D(-2,-8,-5) . Составить уравнение сферы, если известно, что эти точки лежат на ее поверхности.

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

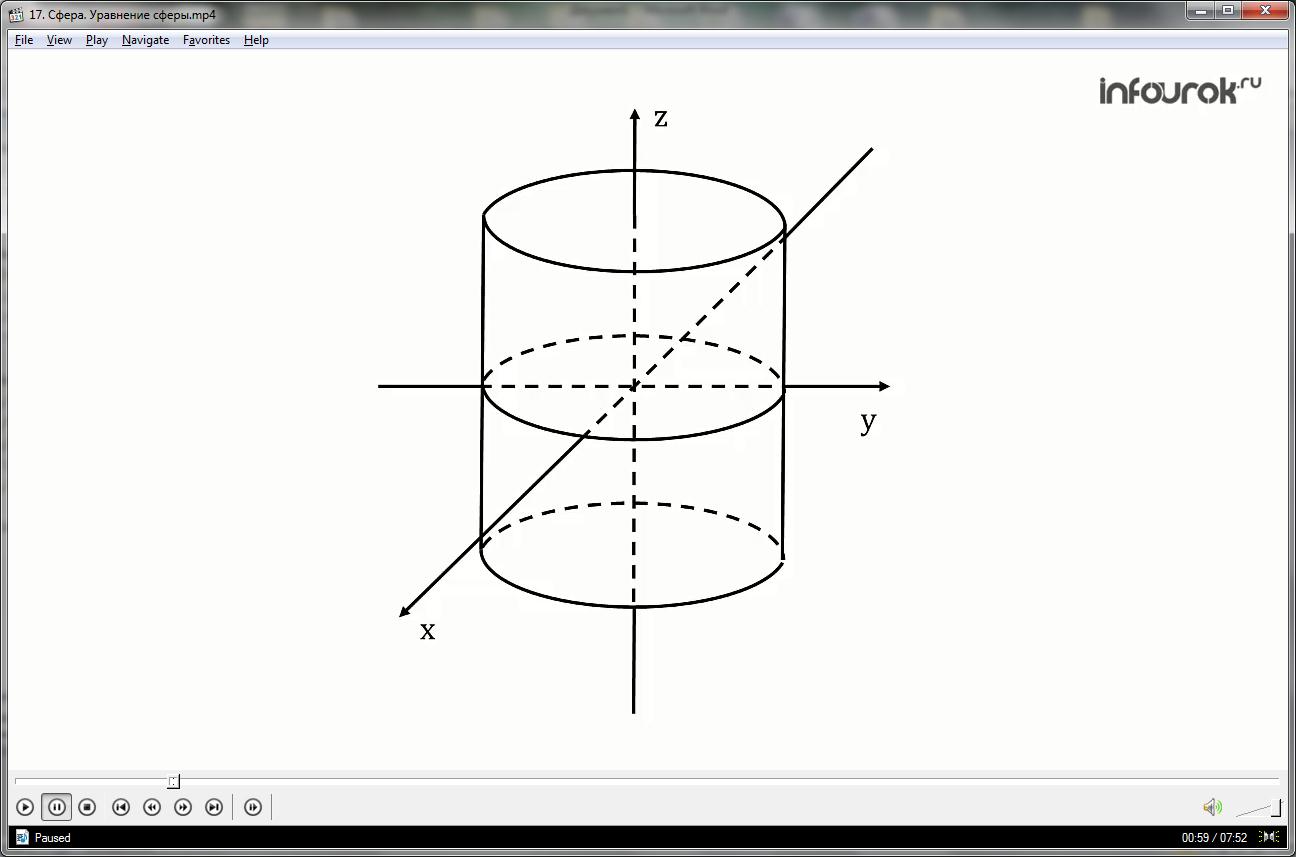
Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

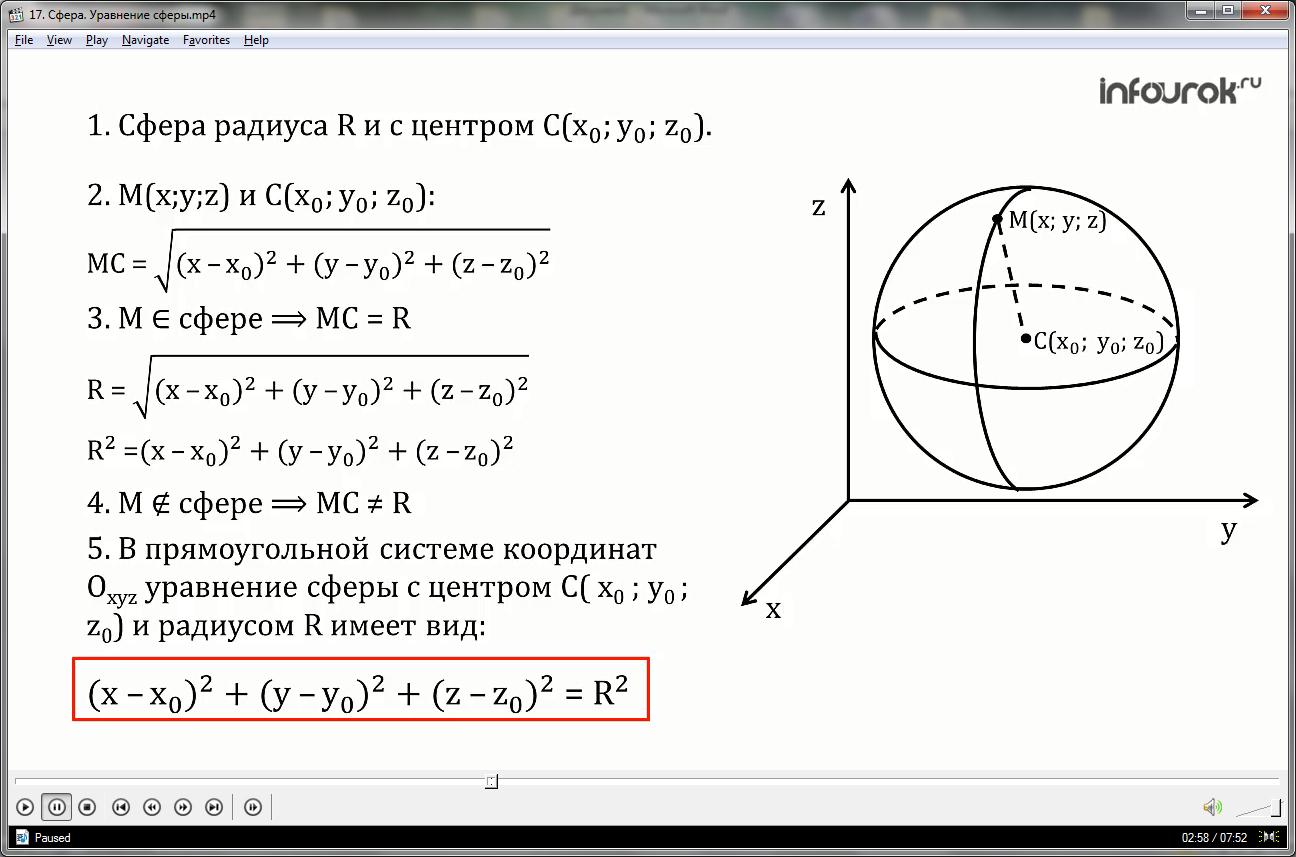
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

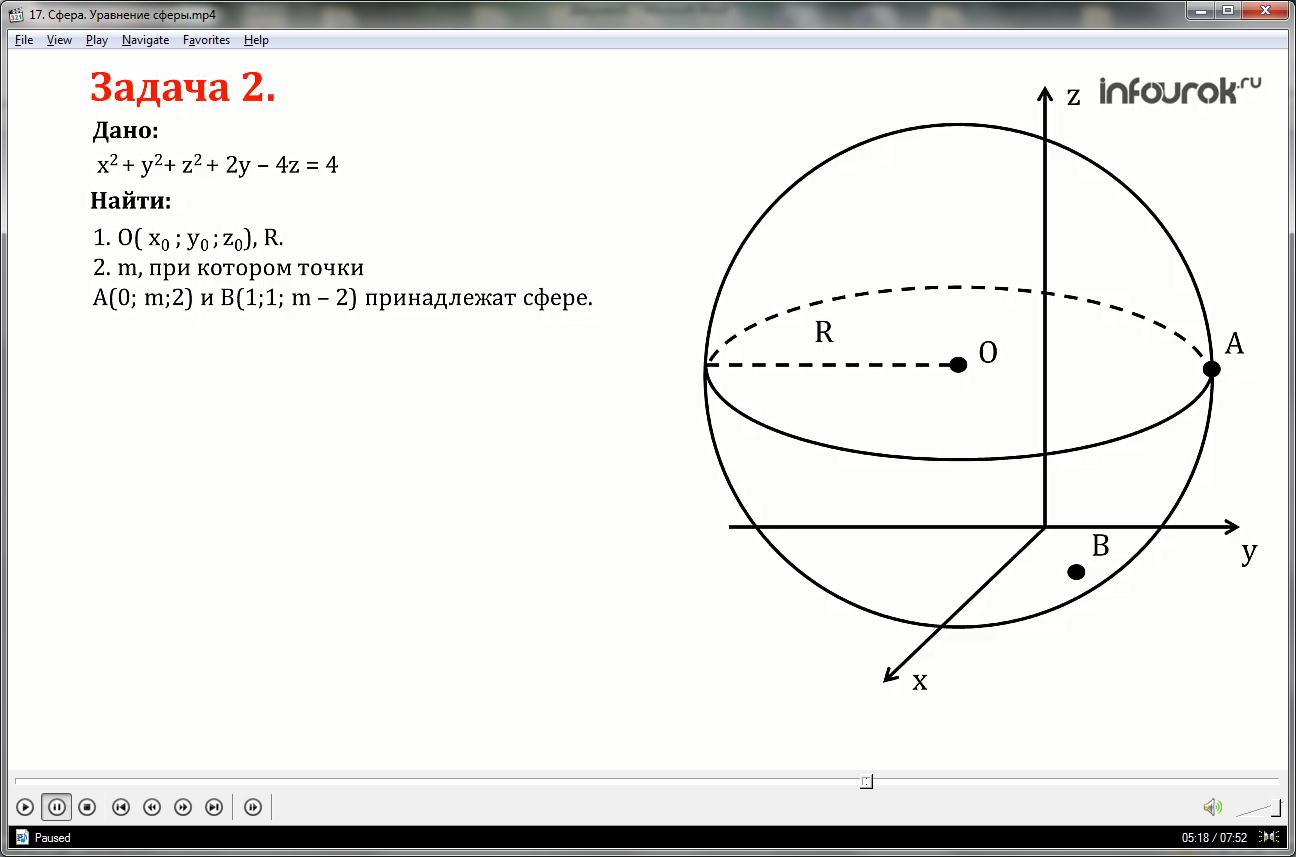
Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

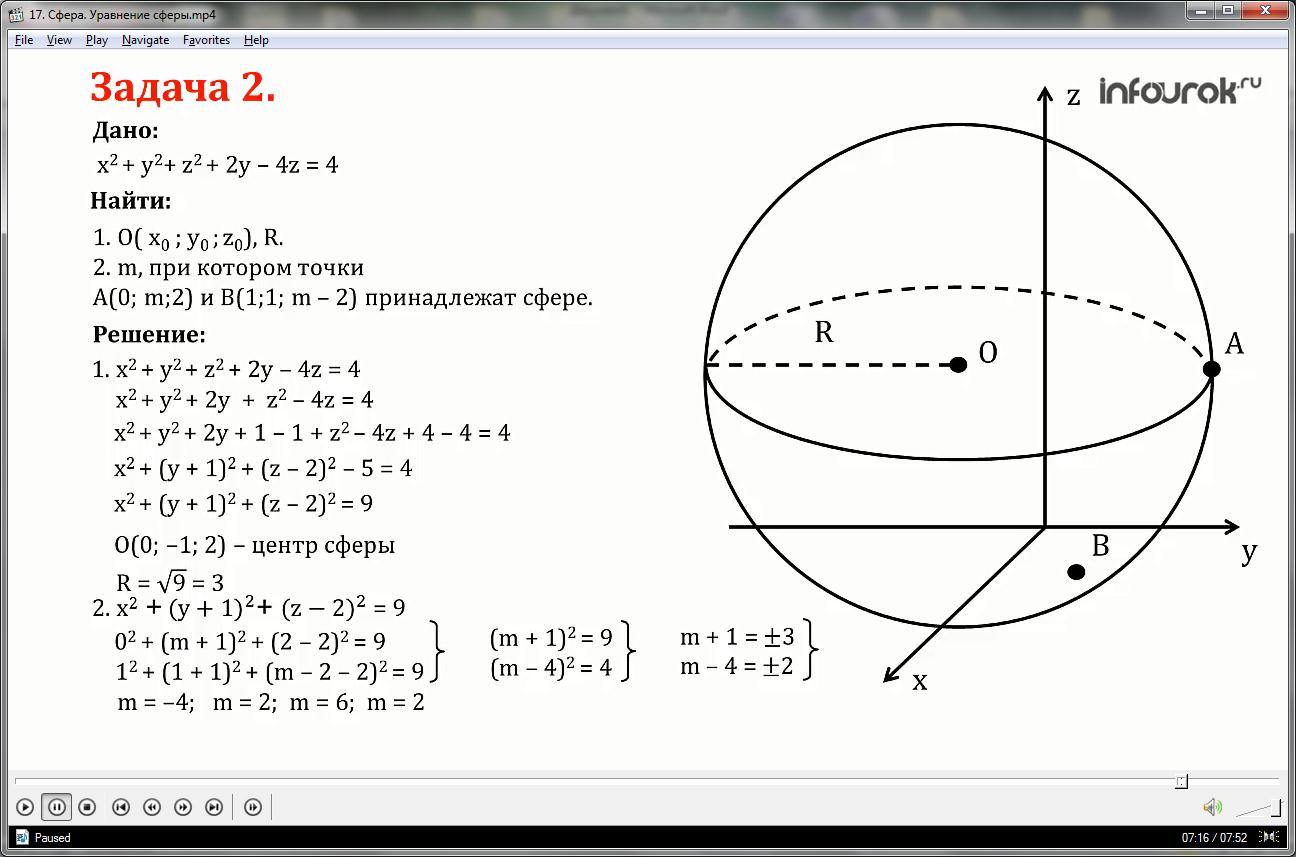
1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

53883

1003

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Презентация к уроку №2 на тему «Уравнение сферы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Раздел: Прямоугольная система координат и векторы в пространстве

Тема урока:
Уравнение сферы
Школа НИШ ФМН г. Астана
Учитель математики: Косова Г.П.
2017-2018 уч. год.

10.4.4
знать уравнение сферы и применять его при решении задач;

воспроизводит определение сферы и шара;
воспроизводит уравнение сферы;
составляет уравнение сферы по заданным условиям;
по уравнению второго порядка восстанавливает уравнение сферы, её центр и радиус;
выясняет принадлежность точек сфере;
определяет точки пересечения сферы с осями координат.
Учащийся

Проверка домашней работы
1.Составить уравнение сферы с центром в точке (-1; 2;3) радиуса 4.

Ответ:
2) Составить уравнение сферы с центром в точке (0; 5;-6) и радиусом равным
.
Ответ:

Работа по группам
Задания группы 1
Сфера задана уравнением:

а) Найдите координаты центра и радиус сферы
б) Найдите значение m, при котором точки
А(m;-3;0) и В(5; -1;m-1) принадлежат данной сфере

3) Найти центр и радиус сферы
х2+у2+z2 -2х+4у-4z-7=0

Центр: (1;-2;2), радиус 4.

4) Составить уравнение сферы с центром в точке (1; 3;-2) , проходящей через начало координат.

б) Найдите значение m, при котором точки А(m;-3;0) и В(5; -1;m-1) принадлежат данной сфере

Ответ: точки А(m;-3;0) и В(5; -1;m-1) принадлежат данной сфере при

Задания группы 2
Диаметр сферы – отрезок АВ с концами
А(2;-1;4) и В(2;7;10)
а) Составьте уравнение сферы

Центр сферы – середина отрезка АВ
О(2;3;7) – центр сферы

б) Найдите кратчайшее расстояние от точки данной сферы до плоскости Oxy
Ответ: 2

Задания группы 3
Сфера задана уравнением
Найдите координаты центра и радиус сферы
Центр: (-2;1;2), радиус 3.

1.Сфера задана уравнением
а) Назовите координаты центра и радиус сферы.
б) Определите, принадлежат ли данной сфере точки А(1;3;-1), В(4;0;2)
Уровень В

2. Сфера с центром в точке О(0;1;-2) проходит через точку А(-3;1;2)
а) Составьте уравнение сферы
б) Найдите координаты точек оси абсцисс, принадлежащих данной сфере
Уровень А

3. Найдите радиус и центр сферы, заданной уравнением:

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

Курс повышения квалификации

Ментальная арифметика: умножение и деление

• Сейчас обучается 81 человек из 37 регионов

Курс повышения квалификации

Педагогические и психологические аспекты подготовки школьников к сдаче ГИА

«Домашнее обучение. Лайфхаки для родителей»

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 857 835 материалов в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 21.05.2018
• 2569
• 87

• 20.05.2018
• 537
• 0

• 20.05.2018
• 351
• 0

• 20.05.2018
• 583
• 0

• 20.05.2018
• 1090
• 0

• 19.05.2018
• 466
• 0

• 19.05.2018
• 265
• 0

• 19.05.2018
• 2599
• 214

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 21.05.2018 4901
• PPTX 329.8 кбайт
• 41 скачивание
• Рейтинг: 1 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Косова Галина Павловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 11 месяцев
• Подписчики: 0
• Всего просмотров: 26553
• Всего материалов: 10

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

«Развитие интеллектуальных способностей школьников путем мнемотехник»

«Современные подходы к профессиональной деятельности педагога»

«Новаторский взгляд репетитора на подготовку к ОГЭ и ЕГЭ в онлайн формате»

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тысячи учителей в Австралии вышли на забастовку

Время чтения: 2 минуты

Онлайн-тренинг «Как закрыть гештальт: практики и упражнения»

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🌟 Видео