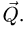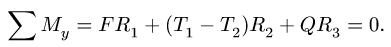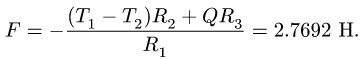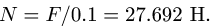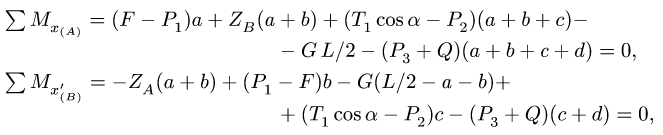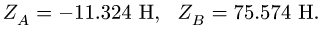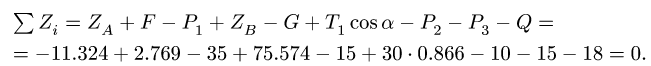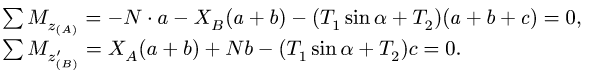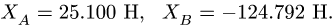Составить уравнение равновесия вала yi 0 (3 видео)

Равновесие вала в теоретической механике

Равновесие вала:

Постановка Задачи. Горизонтальный вал может вращаться в цилиндрических шарнирах. К одному шкиву вала приложено нормальное давление и касательная сила сопротивления, пропорциональная давлению. На шкивы вала действуют известные нагрузки. Найти силу давления и реакции шарниров при условии равновесия вала.

1. Действие каждой из опор заменяем двумя взаимно перпендикулярными реакциями, лежащими в плоскости, перпендикулярной валу.

2. Для определения силы давления составляем уравнение моментов относительно оси вала. Момент силы натяжения ремня, нити и т.п. (наклонной или нет) вычисляем как произведение величины силы на соответствующий радиус со знаком, соответствующим направлению вращения вокруг вала. Уравнение содержит одну неизвестную, которую легко найти.

3. Определяем вертикальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия горизонтальных реакций шарниров. Решаем эти уравнения.

4. Проверяем найденные реакции, составляя уравнение равновесия в проекции на вертикаль.

5. Определяем горизонтальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров.

6. Проверяем горизонтальные реакции, составляя уравнение равновесия в проекции на ось вдоль линии действия горизонтальных реакций.

Задача:

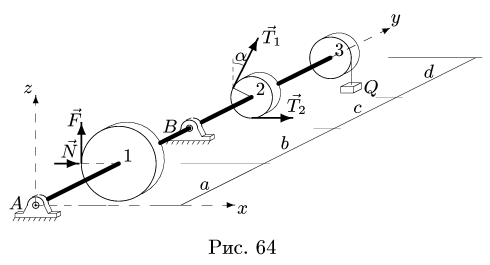
Горизонтальный вал весом G = 15 Н может вращаться в цилиндрических шарнирах А и В (рис. 64). К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F = 0.1 N.

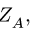
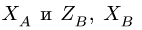
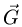
1. Действие цилиндрических опор А и В заменим реакциями (рис. 65). Вес вата приложим в центре. Вес груза изобразим вектором

2. Для определения силы давления составляем уравнение моментов относительно оси вата:

Уравнение содержит одну неизвестную F. Линии действия остальных сил пересекают ось 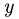и их моменты относительно оси вала равны нулю.

Из полученного уравнения находим

По условию

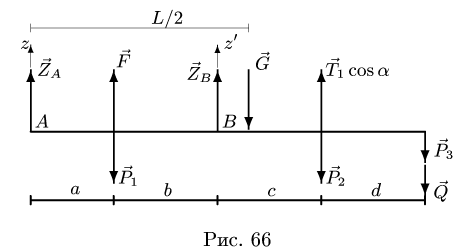
3. Определяем вертикальные реакции шарнирных опор вала. Для этого составляем два уравнения моментов относительно горизонтальных осей, проходящих через шарниры А а В. Рассматриваем для удобства проекцию всех сил на плоскость 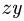(рис. 66). Таким образом вычисление моментов относительно осей сводим к плоской задаче вычисления моментов относительно точек А и В.

Знаки моментов сил определяем как в задачах плоской статики: момент силы, вращающей тело вокруг моментной точки против часовой стрелки считается положительным, по часовой стрелке — отрицательным. Моменты сил, перпендикулярных плоскости 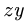(и поэтому не изображенных на рис. 66), относительно любой ее точки равны нулю.

находим

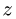
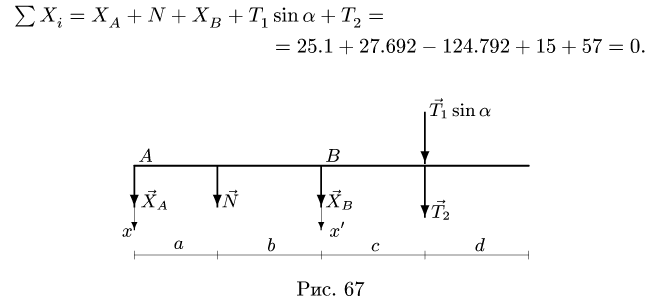
4. Проверяем правильность нахождения вертикальных реакций, составляя уравнение равновесия в проекции на ось (рис. 66):

5. Определяем горизонтальные реакции опор вата. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров. Рассматриваем горизонтальную проекцию силовой схемы (рис. 67):

Решая уравнения, находим

6. Проверяем правильность нахождения горизонтальных реакций, составляя уравнение равновесия в проекции на ось х вдоль линии действия горизонтальных реакции:

Результаты расчетов в 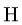заносим в таблицу:

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

Определение усилий в стержнях, поддерживающих плиту
Тело на сферической и стержневых опорах
Приведение системы сил к простейшему виду
Плоское движение тела
Задачи на вращательное движение тела
Равновесие тяжелой рамы
Расчет составной конструкции
Момент силы относительно оси

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Определение реакций опор простой рамыСкачать

Пример выполнения расчетно-графической работы.

На вал (рис 1,а) жестко насажены шкив 1 и колесо 2. Определить силы F₂, F_r₂= 0,4 F₂, а также реакции опор А и В, если F₁= 100 Н.

Решение:

1. Изображаем вал со всеми действующими на него силами, а также оси координат (рис. 1,б).

2. Определяем F₂ и F_r₂. Из условия равновесия вала, имеющего неподвижную ось:

Σ M_z (F_i)=0;

F_r₂= 0,4 F₂= 0,4 300= 120 Н

3. Составляем шесть уравнений равновесия:

Σ M_x (F_i)=0; Σ M_x = -R_By AB+F₂ AD=0 ; (1)

Σ M_y (F_i)=0; Σ M_y = 3F₁ AC+F_r2 AD-R_Bx AB =0 ; (2)

Σ M_x1 (F_i)=0; Σ M_x1 = R_Ay AB-F₂ DB=0 ; (3)

Σ M_y1 (F_i)=0; Σ M_y1 = R_Ax AB-3F₁ CB- F_r2 DB =0 ; (4)

4. Решаем уравнения (1), (2), (3), (4) и определяем реакции опор:

из (1) R_By= ;

из (2) R_Bx= ;

из (3) R_Ay= ;

из (4) R_Ax=

5. Проверяем правильность найденных реакций опор. Используем уравнение (5):

Следовательно, реакции R_Ax и R_Bx определены верно. Используем уравнение (6):

Следовательно, реакции R_Ay и R_By определены верно.

Расчетно-графическая работа №4

по теме:

«Построение эпюр продольных сил, нормальных напряжений и определение деформации бруса при растяжении и сжатии»

Последовательность решения задачи:

1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, и места изменения размеров поперечного сечения.

2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N), построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провестилинии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т. е. эпюра на данном участке изображается прямой, параллельной оси бруса.

4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Пример.Для данного ступенчатого бруса (рис. 1, а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если Е=2*10 5 МПа;

Решение:

F₁ = 30KH = 30·10 3 Н; F₂= 38·10 3 Н;

Расчетно-графическая работа №5

по теме:

«Проектный расчет вала, работающего на кручение,

Из условий прочности и жесткости»

Последовательность решения задачи:

1. Определить внешние скручивающие моменты по формуле М = Р/ώ, где Р — мощность, ώ — угловая скорость.

2. Определить уравновешивающий момент, используя уравнение равновесия ΣM_i = 0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.

3. Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.

4. Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала круглого (для четных вариантов) или кольцевого (для нечетных вариантов) сечения из условия прочности и жесткости. Для кольцевого сечения вала принять соотношение диаметров c = d_o/d, где d_о — внутренний диаметр кольца; d — наружный диаметр кольца.

Видео:Равновесие вала. Реакции опорСкачать

Примеры решения задач

Пример 1. На тело в форме куба с ребром а = 10 см действуют три силы (рис. 7.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.

Решение

1. Моменты сил относительно оси Ох:

2. Моменты сил относительно оси Оу.

Пример 2. На горизонтальном валу закреплены два колеса, г₁ = 0,4 м; г₂ = 0,8 м. Остальные размеры — на рис. 7.7. К колесу 1 приложена сила F₁, к колесу 2 — силы F₂ = 12 кН, F₃ = 4кН.

Определить силу F₁ и реакции в шарнирах А и В в состоянии равновесия.

1. При равновесии выполняются шесть уравнений равновесия.

Уравнения моментов следует составлять относительно опор А и В.

Моменты этих сил относительно соответствующих осей равны нулю.

3. Расчет следует завершить проверкой, использовав дополнительные уравнения равновесия.

Решение

1. Определяем силу F, составив уравнение моментов сил относительно оси Oz:

2. Определяем реакции в опоре А. На опоре действуют две составляющие реакции (Y_A; X_A).

Составляем уравнение моментов сил относительно оси Ох’ (в опоре В).

Поворот вокруг оси Ох’ не происходит:

Знак «минус» означает, что реакция направлена в противоположную сторону.

Поворот вокруг оси Оу’ не происходит, составляем уравнение моментов сил относительно оси Оу’ (в опоре В):

3.Определяем реакции в опоре В. На опоре действуют две составляющие реакции (X_B, Y_B). Составляем уравнение моментов сил относительно оси Ох (опора А):

Составляем уравнение моментов относительно оси Оу (опора А):

4.Проверка. Используем уравнения проекций:

Расчёт выполнен верно.

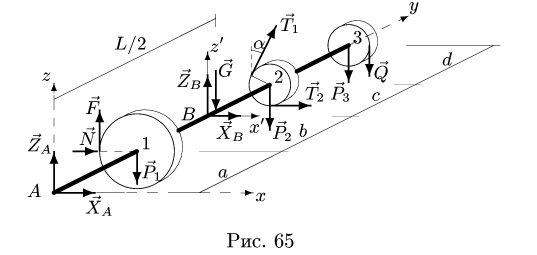
Пример 3. Определить численное значение силы P₁, при котором вал ВС (рис. 1.21, а) будет находиться в равновесии. При найденном значении силы Р₁определить опорные реакции.

Действующие на зубчатые колеса силы Ри Р₁направлены по касательным к начальным окружностям колес; силы Т и Т₁ — по радиусам колес; силы А₁ параллельны оси вала. Т = 0,36Р, 7Т₁ = Р₁; А₁ = 0,12P₁.

Решение

Опоры вала, изображенные на рис. 1.21, а, надо рассматривать как пространственные шарнирные опоры, препятствующие линейным перемещениям в направлениях осей и и v (выбранная система координат показана на рис. 1.21, б).

Освобождаем вал от связей и заменяем их действие реакциями V_В, Н_В,V_C, Н_С (рис. 1.21, б). Получили пространственную систему сил, для которой составляем уравнения равновесия, пользуясь выбранной системой координат (рис. 1.21,6):

где А₁*1,25D/2 — момент относительно оси и силы A₁, приложенной к правому зубчатому колесу.

Моменты относительно оси и сил Т₁ и А₁ (приложенных к среднему зубчатому колесу), Р₁ (приложенной к правому зубчатому колесу) и Р равны нулю, так как силы Р, T₁, Р₁ параллельны оси и, а сила А₁ пересекает ось и.

Составим проверочное уравнение:

следовательно, реакции V_B и V_С определены верно;

где А₁* 1,25D/2 — момент относительно оси v силы А₁, приложенной к среднему зубчатому колесу.

Моменты относительно оси v сил Т, Р₁ (приложенной к среднему зубчатому колесу), А₁ и Т₁ (приложенных к правому зубчатому колесу) равны нулю, так как силы Т, Р₁, Т₁ параллельны оси v, сила А₁ пересекает ось v.

Составим проверочное уравнение:

следовательно, реакции Н_В и Н_С определены верно.

В заключение отметим, что опорные реакции получились со знаком плюс. Это указывает на то, что выбранные направления V_B, Н_В, V_C и Н_С совпадают с действительными направлениями реакций связей.

Пример 4. Сила давления шатуна парового двигателя Р = 25 кН передается на середину шейки коленчатого вала в точке D под углом α = 30° к горизонту при вертикальном расположении щек колена (рис. 1.22). На конец вала насажен шкив ременной передачи. Натяжение ведущей ветви ремня в два раза больше, чем ведомой, т.е. S₁ = 2S₂. Сила тяжести маховика G = 10 кН.

Определить натяжения ветвей ременной передачи и реакции подшипников А и В, пренебрегая массой вала.

Решение

Рассматриваем равновесие горизонтального коленчатого вала со шкивом. Прикладываем в соответствии с условием задачи заданные силы Р, S₁, S₂ иG. Освобождаем вал от опорных закреплений и заменяем их действие реакциями V_A, Н_А, V_B и Н_В. Координатные оси выбираем так, как показано на рис. 1.22. В шарнирах А и В не возникает реакций вдоль оси w, так как натяжение ветвей ремня и все остальные силы действуют в плоскостях, перпендикулярных этой оси.

Составим уравнения равновесия:

Кроме того, по условию задачи имеем еще одно уравнение

Таким образом, здесь имеется шесть неизвестных усилий S_1, S₂, Н_А, V_A, Н_В иV_B и шесть связывающих их уравнений.

Уравнение проекций на ось w в рассматриваемом примере обращается в тождество 0 = 0, так как все силы лежат в плоскостях, перпендикулярных оси w.

Подставляя в уравнения равновесия S₁=2S₂ и решая их, находим:

Значение реакции Н_В получилось со знаком минус. Это значит, что в действительности ее направление противоположно принятому на рис. 1.22.

Контрольные вопросы и задания

1. Запишите формулы для расчета главного вектора пространственной системы сходящихся сил.

2. Запишите формулу для расчета главного вектора пространственной системы произвольно расположенных сил.

3. Запишите формулу для расчета главного момента пространственной системы сил.

4. Запишите систему уравнений равновесия пространственной системы сил.

5. Какое из уравнений равновесия нужно использовать для определения реакции стержня R₁ (рис. 7.8)?

6. Определите главный момент системы сил (рис. 7.9). Точка приведения — начало координат. Координатные оси совпадают с ребрами куба, ребро куба равно 20 см;F₁ — 20кН;F₂ — 30кН.

7. Определите реакцию Хв (рис. 7.10). Вертикальная ось со шкивом нагружена двумя горизонтальными силами. Силы F₁ и F₂ параллельны осиОх. АО = 0,3 м; ОВ = 0,5 м; F₁ = 2кН; F₂ = 3,5 кН.