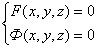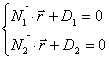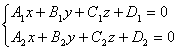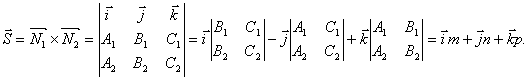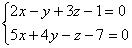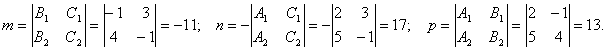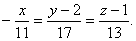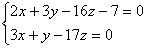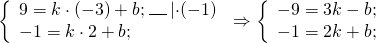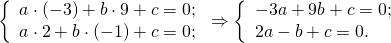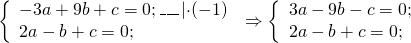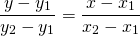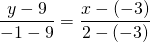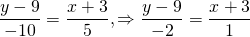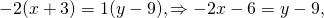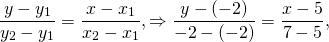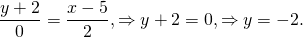Составить уравнение прямой проходящей через точки и найти ее направляющие косинусы (8 видео)

Уравнение прямой проходящей через две точки

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

каноническое уравнение,
параметрическое уравнение,
общее уравнение прямой,
уравнение прямой с угловым коэффициентом,
уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Видео:§7 Направляющие косинусы вектораСкачать

Составить уравнение прямой проходящей через точки и найти ее направляющие косинусы

Уравнение линии в пространстве.

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F ( x , y , z ) = 0 и Ф ( x , y , z ) = 0 – уравнения поверхностей, пересекающихся по линии L .

Тогда пару уравнений

назовем уравнением линии в пространстве.

Уравнение прямой в пространстве по точке и

Возьмем произвольную прямую и вектор ( m , n , p ), параллельный данной прямой. Вектор называется направляющим вектором прямой.

На прямой возьмем две произвольные точки М ₀ ( x ₀ , y ₀ , z ₀ ) и M ( x , y , z ).

M ₁

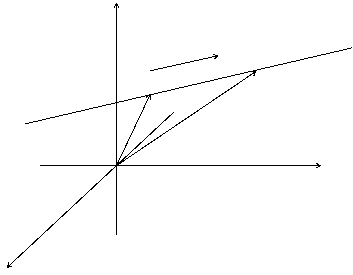
Обозначим радиус- векторы этих точек как и , очевидно, что — = .

Т.к. векторы и коллинеарны , то верно соотношение = t , где t – некоторый параметр.

Итого, можно записать: = + t .

Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

Преобразовав эту систему и приравняв значения параметра t , получаем канонические уравнения прямой в пространстве:

Определение. Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:

; .

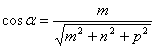
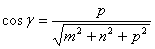
Отсюда получим: m : n : p = cos a : cos b : cos g .

Числа m , n , p называются угловыми коэффициентами прямой. Т.к. — ненулевой вектор, то m , n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.

Уравнение прямой в пространстве, проходящей

через две точки.

Если на прямой в пространстве отметить две произвольные точки M ₁( x ₁, y ₁, z ₁) и M ₂( x ₂, y ₂, z ₂), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

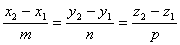
Кроме того, для точки М ₁ можно записать:

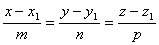
Решая совместно эти уравнения, получим:

Это уравнение прямой, проходящей через две точки в пространстве.

Общие уравнения прямой в пространстве.

Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.

Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:

× + D = 0, где

— нормаль плоскости; — радиус- вектор произвольной точки плоскости.

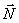
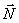
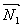
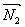
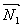
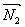
Пусть в пространстве заданы две плоскости: × + D ₁ = 0 и × + D ₂ = 0, векторы нормали имеют координаты: ( A ₁ , B ₁ , C ₁ ), ( A ₂ , B ₂ , C ₂ ); ( x , y , z ).

Тогда общие уравнения прямой в векторной форме:

Общие уравнения прямой в координатной форме:

Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.

Для этого надо найти произвольную точку прямой и числа m , n , p .

При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.

Пример. Найти каноническое уравнение, если прямая задана в виде:

Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.

, т.е. А(0, 2, 1).

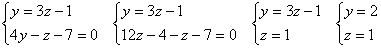
Находим компоненты направляющего вектора прямой.

Тогда канонические уравнения прямой :

Пример. Привести к каноническому виду уравнение прямой, заданное в виде:

Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда :

;

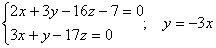
Получаем: A ( -1; 3; 0).

Направляющий вектор прямой: .

Итого:

Видео:Составляем уравнение прямой по точкамСкачать

Составить уравнение прямой, проходящей через две точки

Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.

Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).

1 способ — составим уравнение прямой с угловым коэффициентом.

Уравнение прямой с угловым коэффициентом имеет вид y=kx+b. Подставив координаты точек A и B в уравнение прямой (x= -3 и y=9 — в первом случае, x=2 и y= -1 — во втором), получаем систему уравнений, из которой находим значения k и b:

Сложив почленно 1-е и 2-е уравнения, получим: -10=5k, откуда k= -2. Подставив во второе уравнение k= -2, найдём b: -1=2·(-2)+b, b=3.

Таким образом, y= -2x+3 — искомое уравнение.

2 способ — составим общее уравнение прямой.

Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:

Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.

Умножив первое уравнение системы на -1 и сложив почленно со вторым:

получим: 5a-10b=0. Отсюда a=2b.

Подставим полученное выражение во второе уравнение: 2·2b -b+c=0; 3b+c=0; c= -3b.
Подставляем a=2b, c= -3b в уравнение ax+by+c=0:

2bx+by-3b=0. Осталось разделить обе части на b:

Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:

3 способ — составим уравнение прямой, проходящей через 2 точки.

Уравнение прямой, проходящей через две точки, имеет вид:

Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)

В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.

Если при подстановке координат заданных точек один из знаменателей уравнения

окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.

Составить уравнение прямой, проходящей через две точки C(5; -2) и D(7;-2).

Подставляем в уравнение прямой, проходящей через 2 точки, координаты точек C и D: