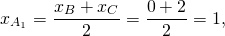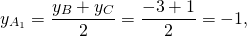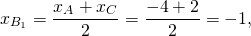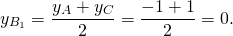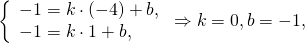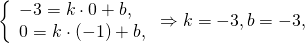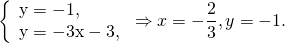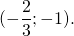Составить уравнение прямой проходящей через начало координат и точку пересечения медиан треугольника

Видео:Уравнения стороны треугольника и медианыСкачать

Точка пересечения медиан треугольника

Как найти точку пересечения медиан треугольника, зная координаты его вершин?

Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.

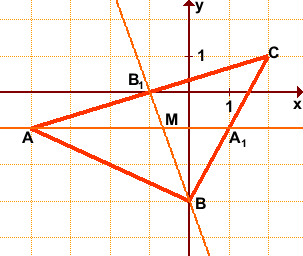
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).

Обозначим середины сторон BC и AC через A₁ и B₁ соответственно. По формулам координат середины отрезка

Составим уравнения медиан AA₁ и BB₁.

Уравнение медианы AA₁ можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A₁(1;-1).

то есть уравнение прямой AA₁ y= -1.

B(0;-3), B₁(-1;0). Найдём уравнение медианы BB₁.

откуда уравнение прямой BB₁ y= -3x-3.

Координаты точки пересечения прямых AA₁ и BB₁ ищем как решение системы уравнений

Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.

Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —

зная координаты A₁(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA₁ в отношении 2:1, считая от точки A.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

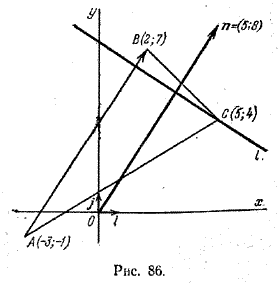
Составить уравнение прямой проходящей через начало координат и точку пересечения медиан треугольника

За нормальный вектор искомой прямой можно взять вектор n = (overrightarrow).
Так как n = (2-(-3); 7 — (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим

или, окончательно, 5х + 8у — 57 = 0.

Видео:Уравнение прямой, проходящей через начало координатСкачать

Координаты точки пересечения медиан треугольника

Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. Обозначаем вершины как как A(x₁;y₁), B(x₂;y₂), C(x₃;y₃),

и вычисляем координаты центра треугольника по формуле: x₀ = (x₁ + x₂ + x₃)/3; y₀ = (y₁ + y₂ + y₃)

5) Координаты начала вектора, если известны координаты самого вектора и его конца, можно найти следующим образом:

Чтобы найти координаты вектора, нужно из координат конца

вычесть соответствующие координаты начала:

Формула для определения длины вектора, если известны

координаты его начала и конца:

Формула для определения длины вектора,

если известны его координаты:

6) Формула длины отрезка:

Периметр треугольника равен AB + BC + AC. Длина отрезка по координатам его концов рассчитывается по формуле

d = √((x2-x1)²+(y2-y1)²), где d— рассчитываемый отрезок, x1,x2 — абсциссы начала и конца отрезка, y1,y2 — ординаты начала и конца отрезка.

7) Как определить, является ли треугольник равнобедренным:

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.

(следствие теоремы косинусов);

· (следствие теоремы косинусов);

· ;

· (теорема о проекциях)

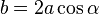
8) Если прямая параллельна оси ОХ и проходит через точку А(2,3), то:

В таком случае прямая будет параллельна оси ординат ОY. Будет иметь вид х=а. В точке А(2; 3) абсцисса равна 2. Значит уравнение прямой имеет вид х=2.

9)Как определить является ли фигура ромбом:

Ромб – это четырёхугольная геометрическая фигура, все стороны которой равны. Противоположные стороны параллелограмма параллельны, а диагонали всегда пересекаются под углом в 90 градусов и делят угол пополам.

Свойства ромба:

• Диагонали ромба пересекаются под прямым углом.
• Диагонали ромба являются биссектрисами его углов.

Параллелограмм, диагонали которого перпендикулярны, является ромбом.

10)Уравнение прямой, проходящей через заданную точку перпендикулярно данной прямой:

Через заданную точку плоскости можно провести единственную прямую, перпендикулярную заданной прямой. Однако, через заданную точку трехмерного пространства можно провести бесконечно много прямых, перпендикулярных заданной прямой. Если построить плоскость , проходящую через заданную точку M₁ перпендикулярно к заданной прямой b, то любая прямая, лежащая в этой плоскости и проходящая через заданную точку M₁, перпендикулярна заданной прямой b.

Таким образом, задача о составлении уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой, имеет практическое значение лишь для случая на плоскости.

11) Способы нахождения углов:

Рассмотрим прямоугольный треугольник:

Задачи на нахождение сторон и углов прямоугольного треугольника решаются по такому алгоритму:

1. Выделяем треугольник, в который входит сторона или угол, который нам нужно найти.

2. Смотрим, какие элементы треугольника нам известны, и с помощью какой тригонометрической функции они между собой связаны.

3. Записываем соотношение, которое связывает между собой эти элементы.

Метод 1 из 3: Посредством двух других углов

1. Сложите известные значения двух углов. Запомните: сумма углов в треугольнике всегда равна 180°. Поэтому, если вы знаете два из трех углов треугольника, то вы легко вычислите третий угол. Первое, что нужно сделать,- это сложить известные значения двух углов. Например, даны углы 80° и 65°. Сложите их: 80° + 65° = 145°.

2.Вычтите сумму из 180°. Сумма углов в треугольнике равна 180°. Поэтому третий угол равен: 180° — 145° = 35°.

3. Запишите ответ. Теперь вы знаете, что третий угол равен 35°. Если вы сомневаетесь, просто проверьте ответ. Сумма трех углов должна быть равна 180°: 80° + 65° + 35° = 180°.

Метод 2 из 3: Посредством переменных

1.Запишите задачу. Иногда вместо точных значений двух углов треугольника в задаче даны только несколько переменных, или переменные и значение угла. Например: найдите угол «х», если два других угла треугольника равны 2x и 24°

Сложите все значения (переменные и числа). х + 2x + 24° = 3x + 24

Вычтите сумму из 180°. Приравняйте полученное уравнение к 0. Вот как это делается:

· Найдите х. Для этого обособьте члены с переменной на одной стороне уравнения, а числа – на другой: 156° = 3x. Теперь разделите обе части уравнения на 3, чтобы получить х = 52°. Это означает, что третий угол треугольника равен 52°. Другой угол, данный в условии как 2x, равен: 2*52° = 104°

· Проверьте ответ. Для этого сложите числовые значения всех трех углов (сумма должна быть равна 180°): 52° + 104° + 24° = 180°.

Дата добавления: 2015-09-12 ; просмотров: 34 | Нарушение авторских прав

💡 Видео

Составляем уравнение прямой по точкамСкачать

Уравнение прямой проходящей через начало координат 7 - 8 клСкачать

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

9 класс, 7 урок, Уравнение прямойСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Уравнение окружности (1)Скачать

Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

Найти точку пересечения прямой и плоскостиСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать