С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
- Предупреждение
- Расстояние от точки до прямой − теория, примеры и решения
- 1. Расстояние от точки до прямой на плоскости
- 2. Расстояние от точки до прямой в пространстве
- Решение задач по математике онлайн
- Калькулятор онлайн. Вычисление расстояния от точки до прямой
- Расстояние от точки до прямой
- Что называется расстоянием от точки до прямой?
- Расстояние между параллельными прямыми
- Решение задач
- Задача 1
- Задача 2
- Задача 3
- Задача 4
- 🎥 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:9 класс, 7 урок, Уравнение прямойСкачать
Расстояние от точки до прямой − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Расстояние от точки до прямой на плоскости
Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
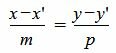 , | (1) |
где q=(m,p) направляющий вектор прямой L.
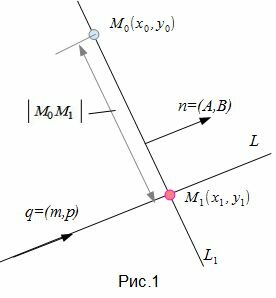
Найдем расстояние от точки M0 до прямой (1)(Рис.1).
 |
Алгоритм нахождения расстояния от точки M0 до прямой L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
- найти найти расстояние между точками M0 и M1.
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
| A(x−x0)+B(y−y0)=0 | (2) |
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
| m(x−x0)+p(y−y0)=0 | (3) |
| mx+py−mx0−py0=0 | (4) |
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
 |
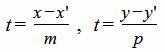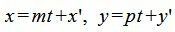 | (5) |
Подставим значения x и y в (4):
| m(mt+x’)+p(pt+y’)−mx0−py0=0 |
| m 2 t+mx’+p 2 t+py’−mx0−py0=0 |
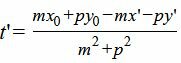 | (6) |
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
Далее находим расстояние между точками M0 и M1 используя формулу:
 . | (7) |
Пример 1. Найти расстояние от точки M0(−6, 2) до прямой
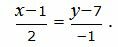 | (8) |
Направляющий вектор прямой (8) имеет вид:
Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x0, y0, x’, y’ в (6):
 |
 |
 , |
Подставляя значение t в (5), получим:
 |
Вычислим расстояние между точками M0(-6, 2) и M1
 |
Упростим и решим:
  |
Расстояние от точки M0(-6, 2) до прямой (8) :
 |
2. Расстояние от точки до прямой в пространстве
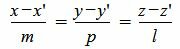 , | (9) |
где q=(m, p, l) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (9)(Рис.2).
 |
Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
- найти расстояние между точками M0 и M1.
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (10) |
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:
| m(x−x0)+p(y−y0)+l(z−z0)=0 |
| mx+py+lz−mx0−py0−lz0=0 | (11) |
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (9):
 |
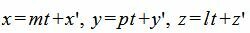 | (12) |
Подставим значения x и y в (11):
| m(mt+x’)+p(pt+y’)+l(lt+z’)−mx0−py0−lz0=0 |
| m 2 t+mx’+p 2 t+py’+l 2 t+ly’−mx0−py0−lz0=0 |
 | (13) |
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M0 на прямую L:
| M1(x1, y1, , z1), |
Далее вычисляем расстояние между точками M0 и M1 используя формулу
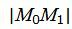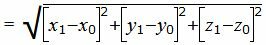  , | (14) |
которое является расстоянием между точкой M0 и прямой (9).
Пример 2. Найти расстояние от точки M0(1, 2, 1) до прямой
 | (15) |
Направляющий вектор прямой (15) имеет вид:
Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (13):
 |
 |
 |
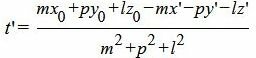Подставляя значение t=t’ в (12), получим координаты точки M1:
 , |
 , |
 . |
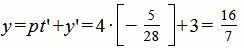Далее, используя формулу (14) вычисляем расстояние от точки M0 до прямой (15):
  . |
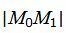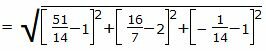Упростим и решим:
   . |
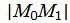Расстояние от точки M0(1, 2, 1) до прямой (15) :
Видео:Составляем уравнение прямой по точкамСкачать
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Калькулятор онлайн.
Вычисление расстояния от точки до прямой
Этот калькулятор онлайн вычисляет расстояние от точки до прямой заданной в каноническом виде (для трехмерного случая):
Онлайн калькулятор для вычисления расстояния от точки до прямой не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac )
Видео:Расстояние от точки до прямойСкачать
Расстояние от точки до прямой
О чем эта статья:
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Что называется расстоянием от точки до прямой?
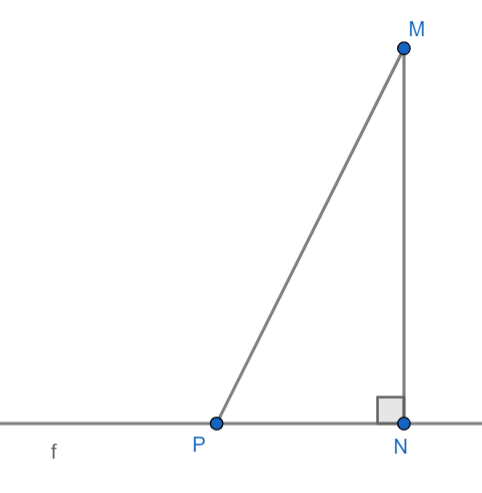
Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на прямую. Перпендикуляр — это кратчайшее расстояние от точки до прямой.
Доказать это очень просто. Из точки M на прямую f мы опустим перпендикуляр MN и произвольную прямую MP, которая также называется наклонной. А по свойству мы помним, что наклонная всегда больше перпендикуляра, что и требовалось доказать.
Расстояние между точкой M и прямой f на плоскости обозначают так:
Видео:Видеоурок "Нормальное уравнение прямой"Скачать
Расстояние между параллельными прямыми
А если нужно вычислить расстояние между двумя параллельными улицами — какое математическое понятие поможет в этом случае? Конечно, вы уже догадались, что это расстояние между параллельными прямыми.
Расстоянием между параллельными прямыми называется расстояние от какой-либо прямой до другой прямой на плоскости.
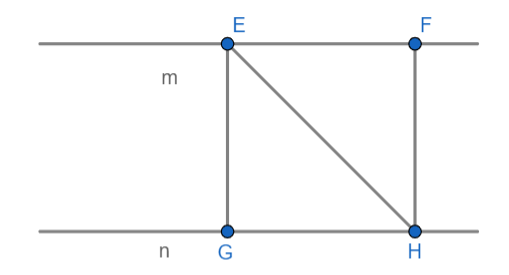
Убедимся в верности этого утверждения — рассмотрим параллельные прямые m и n. На прямой m выберем две точки E и F, опустим из них перпендикуляры на прямую n, точки пересечения перпендикуляров с прямой n обозначим буквами G и H, а также соединим E и H отрезком.
Рассмотрим треугольники GEH и EFH: сторона EH — общая, (как накрест лежащие углы). Следовательно, по гипотенузе и острому углу. А из свойства равных треугольников мы знаем, что будут равны и соответствующие элементы, например, EG = FH.
Делаем вывод, что расстоянием между параллельными прямыми на плоскости является длина их общего перпендикуляра, причем выбор перпендикуляра может быть произвольным.
Расстояние между двумя прямыми m и n обозначается так: .
Видео:18. Расстояние от точки до прямой в пространствеСкачать
Решение задач
Применим полученные знания, решив несколько задач.
Задача 1
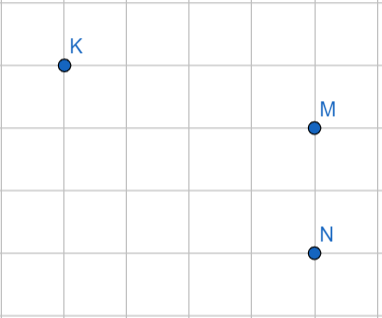
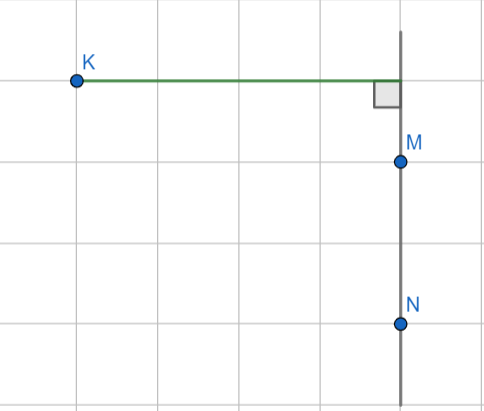
На клетчатой бумаге с размером клетки отмечены точки K, M и N. Чему равно расстояние от точки K до прямой MN?
Как вы помните, чтобы найти расстояние от точки до прямой, нужно из точки на прямую опустить перпендикуляр и вычислить его длину.
Ответ: 4 см.
Задача 2
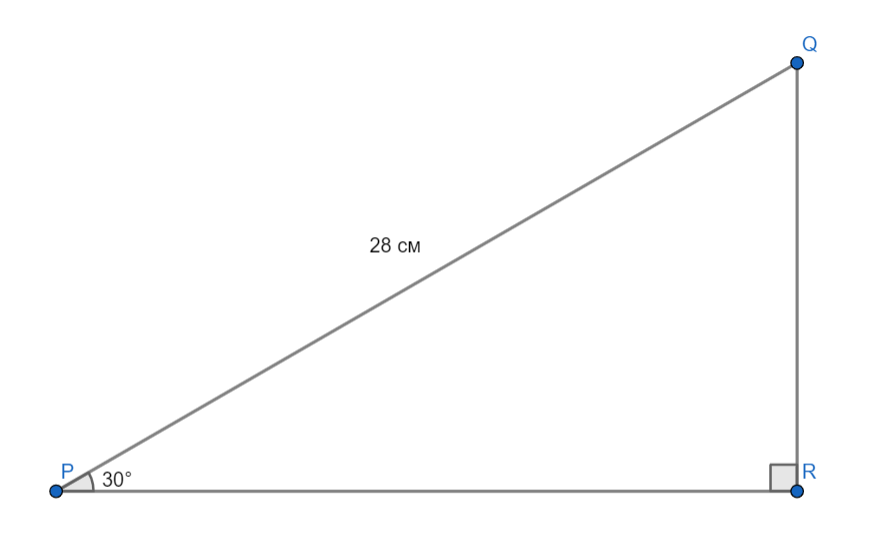
Найдите расстояние от точки Q до прямой PR, пользуясь данными с чертежа.
Из чертежа видно, что отрезок QR перпендикулярен прямой PR, а значит QR — расстояние от точки Q до прямой PR. В прямоугольном треугольнике PQR отрезок QR лежит против угла в , а значит, равен половине гипотенузы, то есть 14 см.
Ответ: 14 см.
Задача 3
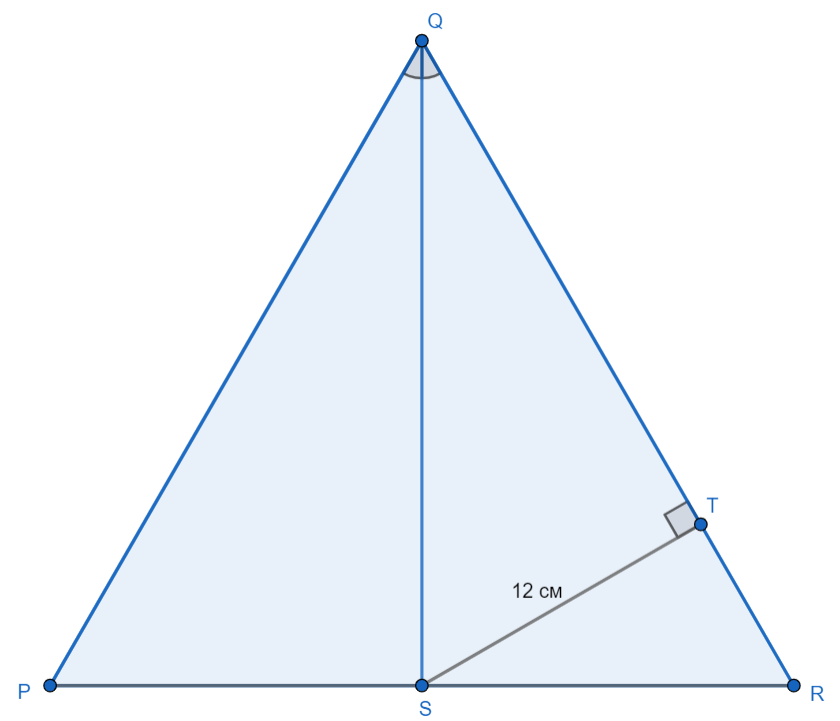
В равностороннем треугольнике PQR проведена биссектриса QS, а ST — расстояние от точки S до прямой QR, равное 12 см. Чему равно расстояние от точки Q до прямой PR?
Поскольку — равносторонний, то , а так как по условию QS — биссектриса, то .
Рассмотрим , так как ST — расстояние от точки S до прямой QR, значит, — прямоугольный. А ST — катет, лежащий против угла в , следовательно, QS = 2ST = 24 см.
Так как — равносторонний, то QS не только биссектриса, но и высота , значит, .
Ответ: 24 см.
А если прямая на плоскости находится так далеко, что провести до нее перпендикуляр физически не получается — что делать в этом случае? Поможет формула расстояния от точки до прямой в координатах.
Пусть формула задана прямой f: ax + by + c = 0 и есть точка M с координатами , тогда формула расстояния от точки до прямой на плоскости выглядит следующим образом:
Задача 4
Найдите расстояние от точки M (36; 6) до прямой f: 6x + 2y − 12 = 0.
Нам не придется даже изображать прямую и точку, а тем более подбирать масштаб, чтобы поместился перпендикуляр, — достаточно воспользоваться формулой:
Конечно, без координат тоже можно вычислить, но вариант выше — самый рациональный и удобный.
На курсах по математике в онлайн-школе Skysmart мы всегда показываем разные способы решений, которые сохранят вам время на контрольной или экзамене. Выберите подходящий по уровню и цели обучения курс и начните заниматься в удовольствие!
🎥 Видео
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
§15 Расстояние от точки до прямойСкачать
Уравнения стороны треугольника и медианыСкачать
Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать
7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать
Уравнение прямой на плоскости. Решение задачСкачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Лекция 24. Расстояние от точки до прямой на плоскости.Скачать
Уравнение прямой.Скачать
Видеоурок "Расстояние от точки до прямой"Скачать
