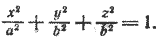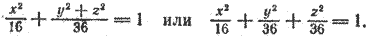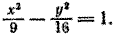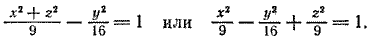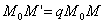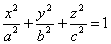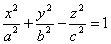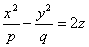Составить уравнение поверхности образованной вращением эллипса x 0 вокруг оси oy (7 видео)

Составить уравнение поверхности образованной вращением эллипса x 0 вокруг оси oy

Глава VI. Простейшие криволинейные поверхности и тела вращения.

§ 75*. Поверхности вращения

1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.

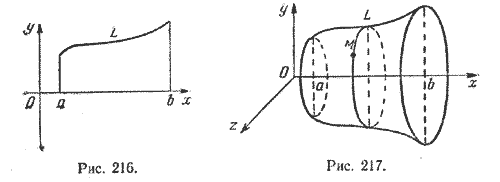
Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение

y = f(x), х [а; b]. (1)

Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).

Очевидно, точка M с координатами (х; у; z), где х [а; b], принадлежит искомой поверхности вращения тогда и только тогда, когда

Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).

Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид

y 2 + z 2 = (f(x)) 2 , х [а; b]. (2)

Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,

В частности, если кривая L задана уравнением

то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид

т. е. просто y 2 заменяем на y 2 + z 2 .

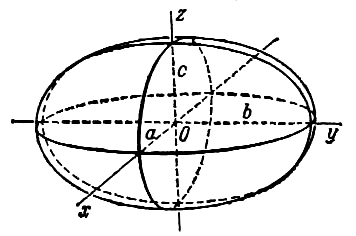
2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.

Пусть в плоскости хОу эллипс задан уравнением

(5)

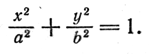
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим

(6)

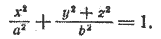
Это уравнение обычно записывают так:

При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:

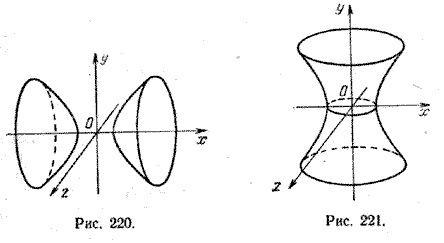
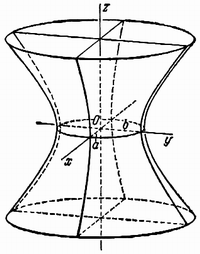
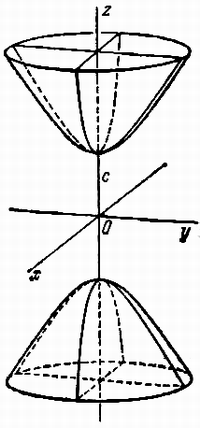
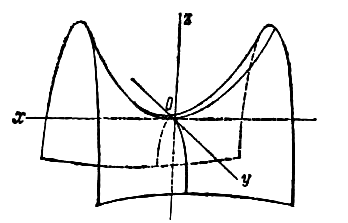
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).

Пусть в плоскости хОу гипербола задана уравнением

(7)

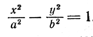
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим

(8)

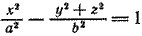
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим

(9)

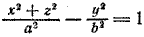
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.

Составим уравнение гиперболы:

Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим

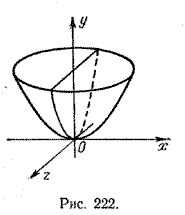
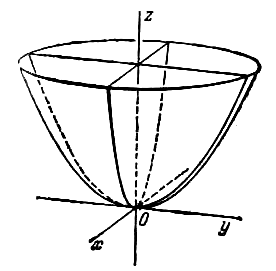
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).

Пусть на плоскости хОу парабола задана уравнением

Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим

Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.

Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).

Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.

Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим

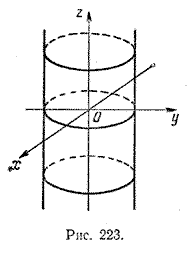
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.

Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение

Эта цилиндрическая поверхность изображена на рис. 223.

Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.

В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим

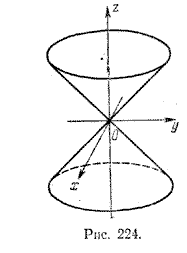
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.

Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид

Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).

Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.

Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.

Содержание

Составить уравнение поверхности образованной вращением эллипса x 0 вокруг оси oy
Глава 46. Поверхности второго порядка
Составить уравнение поверхности образованной вращением эллипса x 0 вокруг оси oy
📺 Видео

Видео:Объем тела, образованного вращением кривой вокруг оси хСкачать

Составить уравнение поверхности образованной вращением эллипса x 0 вокруг оси oy

Видео:§64 Поверхности вращенияСкачать

Глава 46. Поверхности второго порядка

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

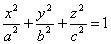
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

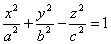
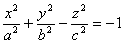
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

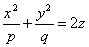
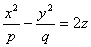
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

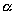
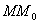
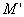
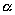
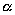
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .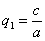

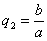
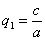
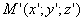
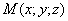
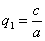
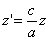
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

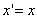
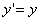
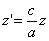
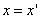
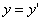
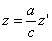
Предположим, что M(x; y; z ) — произвольная точка сферы

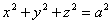
Заменим здесь x, y, z их выражениями (7); получим

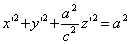
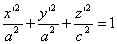
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

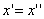
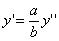
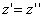
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

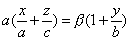
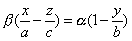
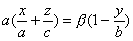
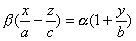
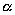
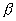
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

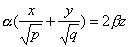
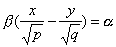
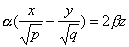
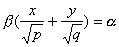
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

Видео:Интегралы №13 Объем тела вращенияСкачать

Составить уравнение поверхности образованной вращением эллипса x 0 вокруг оси oy

Рассмотрим сечение плоскостью у = 0. Получается парабола = z, её ветви направлены вверх, вершина в точке (0, 0, 0).

Рассмотрим сечение плоскостью x = h. Это опять парабола:

Её ветви направлены вниз, вершина смещена по оси OZ на величину . то есть находится в точке . Заметим, что эта точка лежит на параболе

Теперь, изменяя h, видим, что поверхность гиперболического параболоида состоит из парабол, расположенных в плоскостях x = h, вершины которых находятся на параболе .