С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
- Предупреждение
- Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
- Онлайн калькулятор. Уравнение плоскости
- Найти уравнение плоскости
- Ввод данных в калькулятор для составления уравнения плоскости
- Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Теория. Уравнение плоскости.
- Уравнение плоскости через координаты вектора нормали и точки: онлайн-калькулятор
- Как найти уравнение плоскости через координаты вектора нормали и точки с помощью онлайн-калькулятора
- Материалы, которые помогут вам лучше разобраться в теме:
- Уравнение плоскости через точку перпендикулярно вектору онлайн
- 📽️ Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
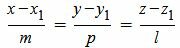 . | (1) |
Построить уравнение плоскости α, проходящей через точку M0 и перпендинулярной прямой L.
 |
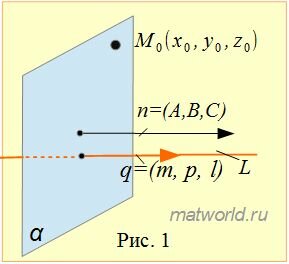Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (3) |
Упростим уравнение (3):
| mx+py+lz+D=0, | (4) |
Таким образом уравнение (4) определяет плоскость, проходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1).
Ответ. Уравнение плоскости прпоходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1) имеет вид (4).
Пример 1. Найти уравнение плоскости α, проходящую через точку M0(3, −1, 2) и перпендикулярной прямой L:
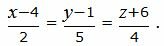 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Направляющий вектор прямой L имеет следующий вид: :
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (8) |
Подставляя координаты точки M0 и направляющего вектора q в (8), получим:
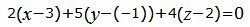 | (9) |
Упростим уравнение (9):
| 2x+5y+4z−9=0. | (10) |
Ответ: Уравнение плоскости, проходящей через точку M0(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:
 | (11) |
Решение. Приведем параметрическое уравнение (11) к каноническому виду:
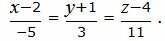 | (11′) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (12) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (13) |
Подставляя координаты точки M0 и направляющего вектора q в (13), получим:
 |
Упростим уравнение (13):
| −5x+3y+11z+77=0. | (14) |
Ответ. Уравнение плоскости, проходящей через точку M0(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
Онлайн калькулятор. Уравнение плоскости
Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.
Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать
Найти уравнение плоскости
Выберите метод решения исходя из имеющихся в задаче данных:
В задаче известны:
Ввод данных в калькулятор для составления уравнения плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки
В зависимости от условий задачи уравнение плоскости можно составить следующими способами:
- Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
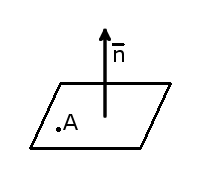
Если заданы координаты точки A( x 1, y 1, z 1) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:2. Уравнение плоскости примеры решения задач #1Скачать
Уравнение плоскости через координаты вектора нормали и точки: онлайн-калькулятор
Плоскость — это бесконечная поверхность с принадлежащими ей прямыми, через которые проходят любые две ее точки. Нормалью к кривой в указанной точке является прямая, расположенная перпендикулярно к касательной прямой в заданной точке кривой.
Если указаны координаты точки A ( x 1 , y 1 , z 1 ) , принадлежащей плоскости, и вектор нормали n = , то уравнение плоскости соответствует формуле:
A ( x — x 1 ) + B ( y — y 1 ) + C ( z — z 1 ) = 0 .
Чтобы найти уравнение плоскости, перпендикулярной вектору онлайн, необходимо:
- указать значение точки A ;
- заполнить значение вектора;
- воспользоваться кнопкой «Рассчитать».
Видео:Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать
Как найти уравнение плоскости через координаты вектора нормали и точки с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Пусть нужно найти уравнение плоскости по вектору нормали к ней и координатам точки, лежащей в плоскости. Для этого в онлайн-калькуляторе просто зададим известную точку и соответствующий вектор (нормаль):
Впишем значения в пустые поля и нажмем «Рассчитать» (значения взяты произвольно):
После этого калькулятор автоматически выдаст подробное решение с ответом:
Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать
Материалы, которые помогут вам лучше разобраться в теме:
Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать
Уравнение плоскости через точку перпендикулярно вектору онлайн
Сервис предназначен для геометрических вычислений, которыми пользуются учащиеся школ и студенты университетов для подготовки к занятиям.
Решение задачи с помощью онлайн-калькулятора имеет преимущества:
- формула в основе автоматических подсчетов дает точный ответ без ошибок и опечаток;
- нет необходимости искать нужный способ расчета;
- пользователю доступно подробное решение;
- производить расчеты можно неограниченное количество раз бесплатно.
Пошаговые вычисления позволяют учащемуся вникнуть в процесс решения задачи по геометрии и справляться с заданиями самостоятельно. Подготовка к занятиям благодаря калькулятору занимает меньше времени и происходит более продуктивно.
📽️ Видео
Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать
Уравнение плоскости. Практическая часть. 11 класс.Скачать
12. Уравнения прямой в пространстве Решение задачСкачать
Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать
Уравнение плоскости через точку и нормальСкачать
7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
