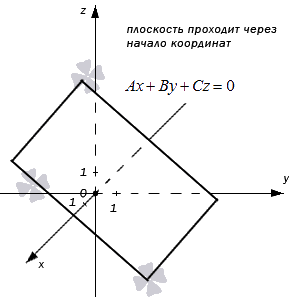
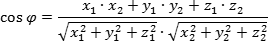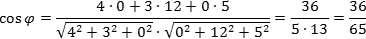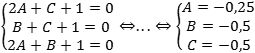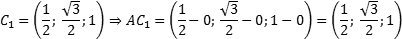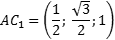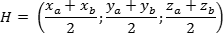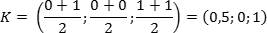Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:
Главная формула — косинус угла φ между векторами a = (x1; y1; z1) и b = (x2; y2; z2):
На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.
Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).
Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:
Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.
Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.
Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:
Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.
Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.
Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!
- Вычисление координат векторов
- Вычисление направляющих векторов для прямых
- Вычисление нормальных векторов для плоскостей
- Координаты середины отрезка
- Общее уравнение плоскости : описание, примеры, решение задач
- Общее уравнение плоскости: основные сведения
- Общее уравнение плоскости, проходящей через точку
- Неполное общее уравнение плоскости
- Онлайн калькулятор. Уравнение плоскости
- Найти уравнение плоскости
- Ввод данных в калькулятор для составления уравнения плоскости
- Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Теория. Уравнение плоскости.
- 💡 Видео
Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Вычисление координат векторов
А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.
Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.
Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:
Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.
Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).
Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).
Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).
Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)
Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Вычисление направляющих векторов для прямых
Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.
Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.
Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:
Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:
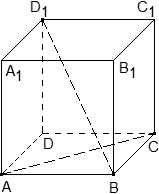
Задача. В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите координаты направляющих векторов этих прямых.
Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1.
Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.
Теперь разберемся с прямой BD1. На ней также есть две точки: B = (1; 0; 0) и D1 = (0; 1; 1). Получаем направляющий вектор BD1 = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).
Ответ: AC = (1; 1; 0); BD1 = (− 1; 1; 1)
Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, проведены прямые AB1 и AC1. Найдите координаты направляющих векторов этих прямых.
Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA1, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.
Для начала разберемся с прямой AB1. Тут все просто: у нас есть точки A = (0; 0; 0) и B1 = (1; 0; 1). Получаем направляющий вектор AB1 = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).
Теперь найдем направляющий вектор для AC1. Все то же самое — единственное отличие в том, что у точки C1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:
Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.
Видео:Уравнение плоскости через 3 точкиСкачать

Вычисление нормальных векторов для плоскостей
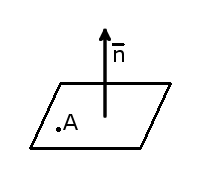
Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.
Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.
Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).
Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:
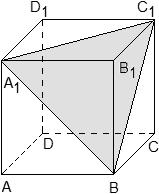
Задача. В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A1, B и C1, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;
Аналогично, для точек B = (1; 0; 0) и C1 = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;
Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.
Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).
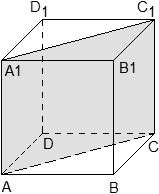
Задача. В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;
Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;
Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).
Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.
Видео:Видеоурок "Уравнение плоскости в отрезках"Скачать

Координаты середины отрезка
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (xa; ya; za) и B = (xb; yb; zb). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
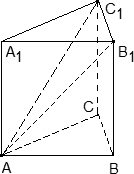
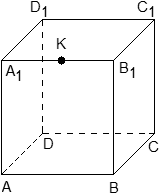
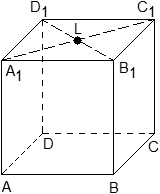
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A1B1. Найдите координаты этой точки.
Поскольку точка K — середина отрезка A1B1, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A1 = (0; 0; 1) и B1 = (1; 0; 1). Теперь найдем координаты точки K:
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A1B1C1D1.
Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A1L = C1L, т.е. точка L — это середина отрезка A1C1. Но A1 = (0; 0; 1), C1 = (1; 1; 1), поэтому имеем:
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
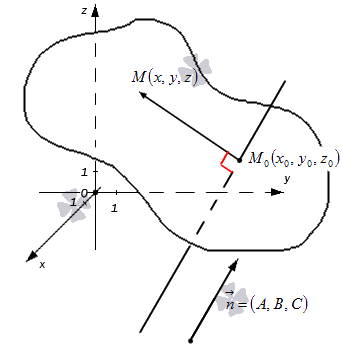
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )
Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.
Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
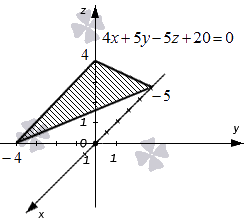
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Общее уравнение плоскости, проходящей через точку
Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.
Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0
Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.
Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:
2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0
Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:
λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0
Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0
- Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:
M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0
Ответ: 3 x + 7 y — 5 z — 26 = 0
Видео:17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
- Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.
- При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0
Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0
Ответ: x — 7 = 0
Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .
Решение
Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .
Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Онлайн калькулятор. Уравнение плоскости
Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.
Видео:3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Найти уравнение плоскости
Выберите метод решения исходя из имеющихся в задаче данных:
В задаче известны:
Ввод данных в калькулятор для составления уравнения плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки
В зависимости от условий задачи уравнение плоскости можно составить следующими способами:
- Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
Если заданы координаты точки A( x 1, y 1, z 1) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
💡 Видео
Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

Уравнение плоскости через 2 точки параллельно векторуСкачать

Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать

Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать

Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать

Уравнение окружности (1)Скачать

5. Нормальное уравнение плоскости выводСкачать

Метод координат Урок №2 2 Нахождение уравнения плоскости по трем точкамСкачать